三、在解题教学中运用变式
数学问题虽然千变万化,但也有其内在的规律,如果在解题中能够领悟从问题提出到问题解决的思维过程,通过反思与总结形成规律性的认识,不仅知道具体问题如何求解,还知道为什么能这样解,也就是说将解题的实践升华到理论的层面上,找到理论支撑,并用于指导今后的解题实践,这样一定会收到满意的效果。
1.题组教学培养学生触类旁通的能力
(1)(05年山东高考题)已知向量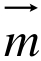 =(cosθ,sinθ),
=(cosθ,sinθ),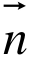 =(
=(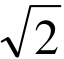 −sinθ,cosθ),θ∈(π,2π)且|
−sinθ,cosθ),θ∈(π,2π)且|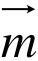 +
+ 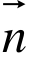 |=
|= 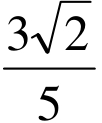 。求cos(
。求cos(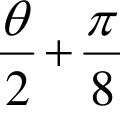 )的值.
)的值.
(2)已知向量
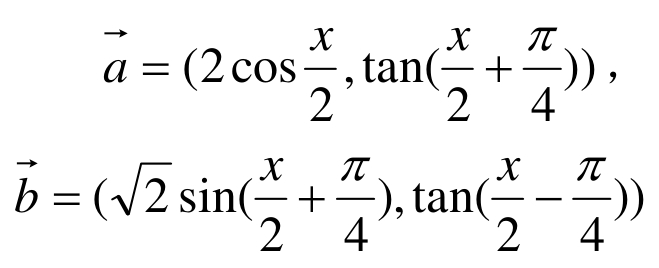
,令f(x)=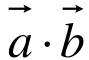 ,是否存在实数x∈(0,π),使f(x)+f′(x)=0,若存在,试求出x的值,若不存在,则证明之.
,是否存在实数x∈(0,π),使f(x)+f′(x)=0,若存在,试求出x的值,若不存在,则证明之.
2.一题多解培养学生思维的灵活性

例 命题“对任何x≥0,都有x 3+1≥2x”是真命题还是假命题?提出你的意见并证明之。
[解1] 考察函数y 1=2x−1(x≥0)与y 2=x 3(x≥0),作出它们的图象(如右图)后考查在同一横坐标条件下,两个图象上相应两点纵坐标的大小,点)1,1(P是公共点,
∵直线y=2x−1的斜率是2,曲线y=x 3在P(1,1)
∵处的切线的斜率k=3x 2|x=1=3,
∴y=2x−1不是曲线y=x 3在P(1,1)处的切线,而是割线。
因此,原命题是假命题。
[解2]设y=x3−2x+1,(x≥0)则y′= 3x2−2,令3x2−2=0,(x≥0)∴x=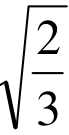 .于是当0≤x<
.于是当0≤x<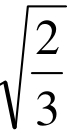 时,y′&lt0;当x>
时,y′&lt0;当x>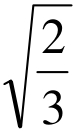 时,y′>0。∴x=
时,y′>0。∴x=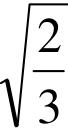 是极小值点.又
是极小值点.又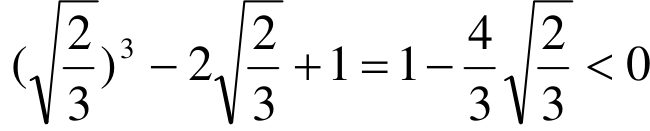 ,所以y=x3−2x+1(x≥0)的值可以是负的,即x3&lt2x-1在x≥0时有解,因此,原命题是假命题。
,所以y=x3−2x+1(x≥0)的值可以是负的,即x3&lt2x-1在x≥0时有解,因此,原命题是假命题。
[解3]∵x3−2x +1= x3−x−x+1=(x−1)(x2+x−1) =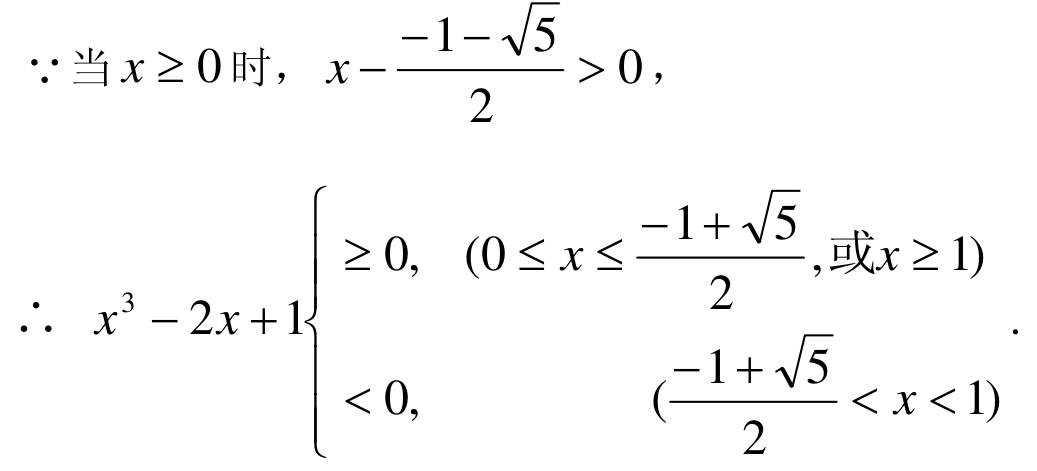
也就是说,当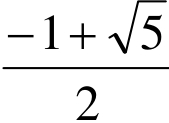 <x<1时, x 3<2x−1.所以,原命题是假命题。
<x<1时, x 3<2x−1.所以,原命题是假命题。
解1、解2运用了导数研究函数,用函数研究不等式的方法,充分体现导数的工具性特征。解3实际上研究函数y=x3−2x+1的值的符号,找到了反例的集合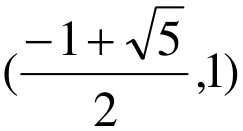 。通过以上剖析,我们只有充分认识函数与导数的工具性价值才能提高复习水平。
。通过以上剖析,我们只有充分认识函数与导数的工具性价值才能提高复习水平。
3.多题一解有助于培养学生归纳、演绎能力,促使学生形成知识链
对课本中的重要概念、例题、习题,充分挖掘其内涵,在多题一解上下工夫,才能使学生在总复习过程中提高复习效果,高考中以不变应万变,找出最佳求解途径。多题一解包含用同一知识和关系解决不同结构的问题(如题目一),还包含挖掘不同题目的内在联系,归纳出统一的解法,形成一种模式.
题目一 设x,y∈R +,且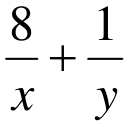 =1,求x+2y的最小值.
=1,求x+2y的最小值.
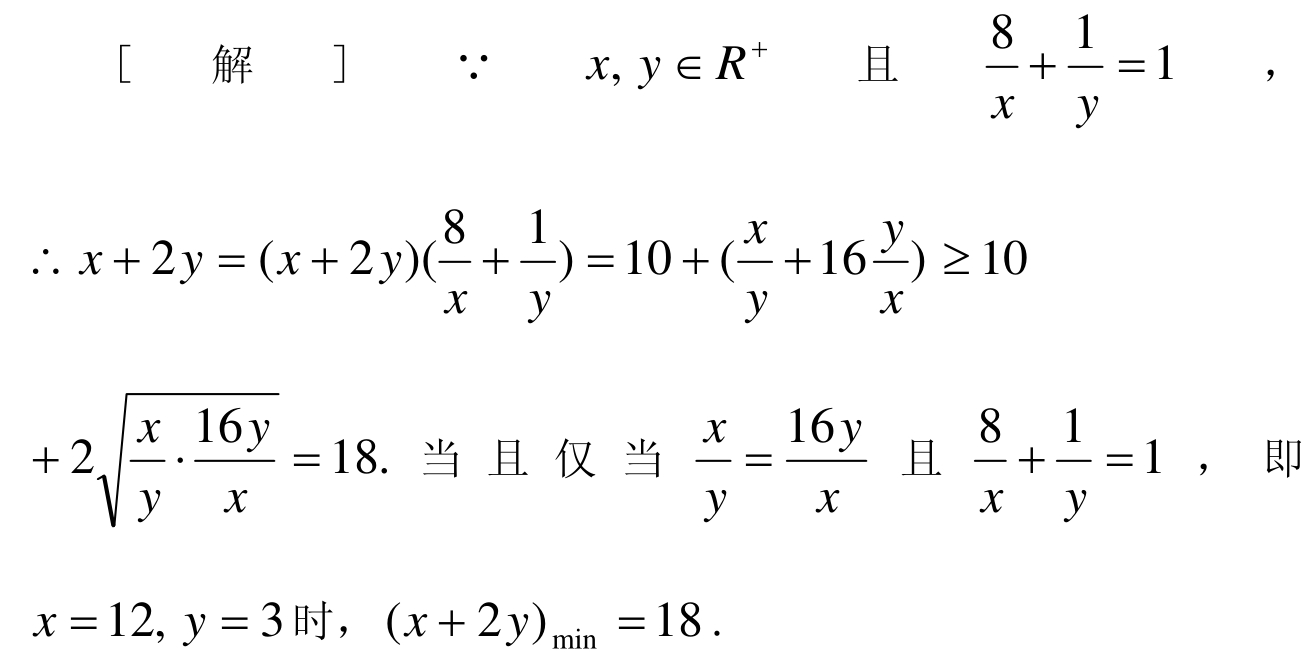
[分析]抓住“1”的代换和均值定理是求一类条件极值的有效策略.
变式1:设x,y∈R +,且xy=x+8y,求x+2y的最小值.
变式2:设x,y∈R +,且y=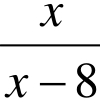 ,求yx2+的最小值.
,求yx2+的最小值.
若认真审视这几个变式中的题设,不难发现:当x,y∈R +时,
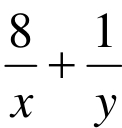 =1⇔xy=x+8y⇔(x−8)(y−1)=8
=1⇔xy=x+8y⇔(x−8)(y−1)=8
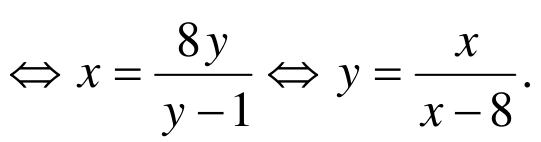
故捕捉解题的“特征信息”,探究题目隐含或显露的惟妙惟肖的关系,是提高解题能力,以一当十、触类旁通的有效策略。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














