欧氏几何如同初恋般美好

欧氏几何如同初恋般美好

数学中有哪些巧合让人眼前一亮？ 

□德安城

我想讲一个故事。这个故事我已经想讲很多年了。

故事的开头，先从几个（数学竞赛党们）耳熟能详的定理说起。

我们都知道，每个三角形都有外接圆和内切圆。它们的圆心，分别称为外心和内心。外心是三角形三条中垂线的交点，而内心是三条内角平分线的交点。这也许是平面几何中，最简单、也最广为人知的巧合。

然而，对于四边形来说，这个性质一般来说就不对了。绝大多数四边形，既没有外接圆，也没有内切圆。

过三个顶点的圆可以不过第四个顶点，和三条边相切的圆也可以不和第四条边相切。

不过总有一些比较幸运的四边形，它们有的有外接圆，有的有内切圆。这些幸运儿们也有着一般的四边形所不具备的优良性质。

比如说，假如一个四边形有内切圆的话，那么它的对角线、对边上的切点的连线四线共点。

这是一个漂亮的巧合。而这个定理的名字，叫做牛顿定理。不错，就是那个发现了万有引力的牛顿。

现在让我们的目光转向更为复杂的图形，六边形。

既然大多数四边形都没有外接圆和内切圆，那大多数的六边形就更没有了。不过，我们只关注那些幸运儿们。它们的身上，也有着不同寻常的巧合。

比如说，对于有外接圆的六边形来说，将它的三组相对的边分别延长相交，所得的三个交点共线。

这里，相对的边这样解释：将六条边顺时针编号为 1,2,3,4,5,6，那么编号为 1 和 4,2 和 5,3 和 6 的三组边分别称作相对的边。严格地说，这里需要每组相对的边都不平行，这样才有交点。

这个定理也十分有名，被称作帕斯卡定理。 这里的帕斯卡，也就是大家都认识的那个帕斯卡。

对于有内切圆的六边形来说，有一个更为简洁优雅的巧合：三条主对角线一定相交于一点。

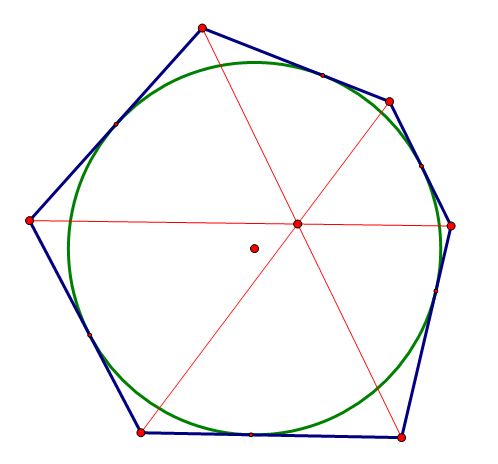
这个定理相对来说较为小众一些，它叫做布里安桑(Brianchon)定理。

注意这个定理和牛顿定理不同，因为对边的切点连线一般不会共点。

到这里为止，数竞党们大概都十分熟悉。下面的才是正题。

如果说有内切圆或外接圆的多边形是幸运儿的话，那么下面所要提到的双心多边形，则可以说是集万千宠爱于一身。

双心多边形，顾名思义，就是既有外心，又有内心的多边形。换句话说，它们既有外接圆，又有内切圆。

在高中的时候，我做过一道竞赛题。它是 1989 年的 IMO 预选题，题目很简洁，也很漂亮。

还记得牛顿定理中四条线所交汇于的那个点吗？这道题要求证明，假如牛顿定理中的四边形是双心四边形，那么这个四线相汇的点也在内心和外心的连线上。

换句话说，就是双心四边形两条对角线、两条对边切点连线、两个圆心的连线这五条线相交于同一点。

这道题看似复杂，其实并不难。假如知道和配极相关的基本结论的话，证明几乎只要三行字。

2011 年 10 月初的一天，当时高三的我看到了上面这道题目。我很快就做了出来。然而，面对如此漂亮的结论，很难不让人浮想联翩：如果把这道题中的四边形换成六边形，会怎么样呢？会不会从五线共点，变成七线共点？

我的直觉告诉我，这个结论对于六边形很可能是错的。因为对于有内切圆的四边形来说，牛顿定理就保证了四线共点，加上一个外接圆的条件，结论只是多一条线（圆心连线）经过这个点。

而对于有内切圆的六边形来说，Brianchon 定理只能保证三线共点，而加上一个外接圆的条件，居然要证明七线共点，也就是多四条线经过这个点。这怎么看都不像是对的。

然而我还是将信将疑地打开了几何画板。 由于我不知道怎么用尺规作出双心六边形，所以只好近似作图，花了好久才画了一个相对精准的图。画完图的一刹那，我就惊呆了：

这特么居然是对的！面对如此漂亮，还是自己猜到的结论，我当即决定试着证证看。

事后看来，这大概是我十年竞赛生涯中做过的最难的两三个几何题之一。不过好在对于六边形来说，有帕斯卡和布里安桑先生们的保佑，问题还不算难得太夸张。尽管费了将近两小时，我还是把它证出来了。

证完之后还没顾得上得意，又一个邪恶的念头从我脑子里冒了出来：既然这个巧合对四边形六边形都成立，会不会对八边形也是成立的呢？

虽然我很希望它是对的，但是冷静下来一想，我还是觉得它怎么都不像对的。因为对于双心六边形来说，Brianchon 保证一个三线共点，Pascal 加上配极又保证一个三线共点，下面只要证明这两个点是同一个，还在圆心连线上就可以了（这也是我的证明思路）。但是到了八边形，Pascal 和 Brianchon 都没法保佑我了，这鬼东西如果是对的谁能证得出来？

然而抱着将信将疑的态度，我还是决定画个图。

是的，和你们想的一样，我又被打脸了。这玩意还真特么就是对的！

这时候我已经在风中凌乱了。我实在是没法想象这鬼东西能怎么证明……然后又一个可怕的念头闪现了出来：这破玩意该不会对所有 2n 边形都成立吧？

我当即决定画个图。既然我都肯定证不出来了，干脆搞个大新闻，直接翻个倍，画 16 边形吧。

后来的事情你们应该也猜到了，半小时之后画完图，我看到的画面是这样的：

我感觉整个人都斯巴达了。

我相信自己一定发现了一个不得了的东西，就拿着这东西去问竞赛圈一个有名的老师。他告诉我，以前在一个数学论坛上有人提到过这个结论，据说（未经证实，我猜很有可能不完全对）某个国家队的大神（不说具体是谁了）也发现过这个结论，还给了一个对于一般情况的物理（黑人问号脸）证明。具体是什么他也不清楚。

尽管没法自己证明这个定理，但我还是深深地被这个结论的壮观与美丽震撼到了。我告诉自己，一定要拿到数学联赛的一等奖，然后保送去北大的数院继续学数学。

然而我并没有如愿。

一周之后的联赛，我只用了三分钟就做出了平面几何大题。尽管其他发挥不太理想，我还是顺利获得了保送。在保送生面试中，北大的招生老师问我，想学什么专业？我毫不犹豫地回答数学。

然后他问：还有别的吗？

我想，他大概是觉得我的联赛分数还不够高吧。所以最后我来到了北大，但没有去成数院，一年之后又阴差阳错地决定不转系，从此远离了真正的数学。

故事还没有结束。一年多前一次偶然的机会，我从知友 @rainbow zyop 那里知道了这个定理的来历。

这个定理被称为彭赛列(Poncelet)定理，是数学家彭赛列在 1813 年法俄战争中，在俄国萨拉托夫的战俘营中发现的（这是有多么闲的蛋疼才能证出这么诡异的定理……）。在彭赛列发现这个定理的两百年后，2014 年 9 月的美国数学月刊上，两位来自苏黎世理工大学的数学家发表了一篇题为《彭赛列定理的一个简单证明》的论文，给出了这个定理的一个初等证明。 不过，这个「简单」的证明长达 12 页。（虽然我知道 12 页的初等证明对于这个问题来说应该已经算短了）

有兴趣的读者可以参考 http://user.math.uzh.ch/halbeisen/publications/pdf/poncelet.pdf 。

我想，这大概算是我见过的数学中最美丽的巧合吧。时隔五年后的今天，我还能想起那个十月的下午，发现这个神奇的结论时激动的心情。我真的很怀念当年参加数学竞赛的日子，那种单纯地喜欢数学之美的时光。

最后我想用罗素的一句话结束这个回答。

欧氏几何如同初恋般美好。

2017-03-01