流体平衡的微分方程及等压面

处于静止(或平衡)状态下的流体，所受的各种外力是处于平衡状态的。本节将根据力的平衡规律，建立流体平衡的微分方程，讨论各种外力相互之间的关系。

3.2.1　流体平衡的微分方程

在静止的密度为ρ的流体中任取一微小平行六面体ABCDEFGH作为隔离体。如图3-3所示。六面体各边分别与直角坐标轴平行，其边长分别为dx、dy、dz。该六面体在质量力和表面力作用下，处于平衡状态。

图3-3　静止流体中平衡状态的微小平行六面体

作用于六面体上的单位质量力在三个坐标轴上的分量分别为fx、fy、fz，六面体的质量为ρdxdydz，则x、y、z方向的质量力分别为

作用于六面体上的表面力是周围流体施加于各个表面上的流体静压力。设六面体中心点M(x，y，z)的流体静压强为p。由于流体静压强为空间坐标的连续函数，则可以通过展开泰勒级数，并略去二阶以上的微量来得到M点附近流体静压强。其中，法线方向为x方向的两个平面ABFE和CDHG中心点处的流体静压强分别为

由于平面ABFE和平面CDHG是微小平面，可以认为整个平面的流体静压强都等于中心点处的流体静压强。于是这两个平面上的流体静压力为

当六面体处于平衡状态时，作用于该六面体上所有外力应满足力的平衡方程，也就是在Ox、Oy、Oz三个坐标轴方向上的分量之和分别等于零。对于Ox轴向有

以ρdxdydz除各项，经简化后得(即，式(3-8)中第一式)

同理，对Oy、Oz两轴向分析也可以给出类似结果(上式中第二、三式)。由此，可以得出流体平衡的微分方程(3-8)。该方程由瑞士学者欧拉于1755年提出，也称为欧拉平衡微分方程。该方程的物理意义是，在静止(平衡)流体中，流体静压强沿某轴向的变化率等于沿该轴向的单位质量力。或者说，在平衡流体中，某轴向只要有质量力的作用，该轴向的流体静压强就会发生变化。

3.2.2　流体平衡微分方程的积分

为求得处于平衡状态的流体中任一点的流体静压强的表达式，必须对流体平衡微分方程(3-8)进行积分。现将式(3-8)中各式分别乘以dx、dy、dz，然后相加并整理后得

上式的左边为流体静压强p的全微分，则有

式(3-10)为流体平衡微分方程的另一表达形式。

对于不可压缩流体，密度ρ等于常数，可以将上式写成

上式左边为函数的全微分，上式右边也必为某一函数W(x，y，z)的全微分。由数学分析可知，上式右边为某一函数的全微分W(x，y，z)的充分必要条件是

需要注意的是，上式可以由流体平衡的微分方程(3-8)推导得到。或者说只要是处于平衡状态的流体(即满足流体平衡微分方程的流体)，就存在空间函数W(x，y，z)。由式(3-11)可得

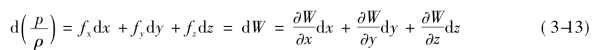
其中

此处给出的空间坐标函数W(x，y，z)在数学、力学中称为势函数，由于与单位质量力f有关，也称为力势函数。存在势函数并同时满足式(3-14)的质量力称为有势力。从上述推导中可见，作用在不可压缩流体上的质量力必须是有势力，不可压缩流体才能保持平衡状态。或者说，要使不可压缩流体保持平衡，只有在有势质量力的作用下才有可能。

改写式(3-13)

并积分，可得

如果已知流体表面或内部任意点处的函数W0、流体静压强p0，代入上式可得C=p0－ρW0，故

式(3-17)就是流体平衡微分方程积分后流体静压强的普遍关系式。式(3-17)表示了在某种有势质量力的作用下，流体静压强的分布规律。从势函数W的引入可知，(W－W0)为空间坐标的函数，与p0无关。由式(3-17)可知，其他各点的压强p均含有流体边界或流体内部某点的已知流体静压强p0。这就是说，处于平衡状态的流体中，无论是流体边界还是流体内部任意一点的流体静压强及其变化量，可以等值地传递到流体内的所有各点。这就是著名的巴斯加原理。

流体平衡微分方程式(3-8)和式(3-10)是解决流体静力学许多问题的基本方程。首先，对流体平衡微分方程进行积分，可以导出流体静压强分布规律的普遍关系式。

3．2．3　等压面

由§3．1已知，在平衡流体中，流体静压强是空间坐标的连续函数。一般来说，不同的点有不同的流体静压强值，但可以找到这样一些点，它们具有相同的流体静压强值，我们将这些点连成的面称为等压面。即流体静压强相等的点组成的面就是等压面。

我们可以利用流体平衡微分方程来讨论等压面。在等压面上，p=常数，则dp=0，代入流体平衡微分方程(3-10)可得等压面微分方程

求解上述方程可以得到反映等压面形状的表达式。

等压面有两个重要性质:

(1)在平衡流体中等压面就是等势面。

显然在等压面上，流体静压强p=常数，即dp=0，代入式(3-15)有ρdW=0，对于不可压缩流体，ρ=常数，则dW=0，积分得W=常数。从而证得在平衡流体中等压面就是等势面。

(2)在平衡流体中等压面与质量力正交。

在平衡流体中任取一等压面A。在质量力F的作用下，有一质量为dm的流体质点M在该等压面A上移动，如图3-4所示。若质点移动距离为ds，并且

其中dx、dy、dz为ds在直角坐标轴上的分量。已知单位质量力为fx、fy、fz，则质量力F为

由理论力学可知，质量力F沿ds移动所做的功W可以写成矢量F与ds的数量积，即

因质点在等压面上移动，由等压面微分方程(3-18)，得

根据功和数量积的定义，当功或数量积等于零时，矢量F和ds正交。由于ds为等压面上任意的微小线段，则质量力F与等压面正交。

图3-4　质点M受质量力的作用在等压面上移动

通常，静止液体的自由表面上各点的压强均为大气压，所以自由表面就是等压面。处于平衡状态下的两种流体(如液体与气体)的交界面也是等压面。根据等压面的第二个性质，对于静止状态的流体，如果作用于流体上的质量力仅仅只是垂直向下的重力，就局部范围而言，等压面一定是水平面，如容器液面、湖面;就大范围而言，作用于流体上的质量力指向地心的引力，则等压面为垂直于地球半径的曲面，如海面、大洋面。