平面上的点和直线

5.3　平面上的点和直线

5.3.1　点和直线属于平面的几何条件

由初等几何知识可以知道，点、直线属于平面的几何条件有如下几点：

（1）如果点在平面内的一条直线上，则该点必属于该直线所在的平面；

（2）如果直线通过平面内的两个点，则该直线必属于这两点所在的平面；

（3）如果直线通过平面内的一个点且平行于平面内的一条已知直线，则该直线必属于这个点和已知直线所确定的平面。

如图5－6所示，E是直线AD上的点，而AD又是平面ABCD内的直线，所以点E是平面ABCD内的点；同理，点F是平面ABCD内的点。直线EF通过平面ABCD内的E和F两个点，所以直线EF属于平面ABCD。直线CG通过平面内的点C且平行于平面内的直线AB，所以直线CG属于平面ABCD。不难看出，A、B、C、D、E、F、G均为平面ABCD内的点，所以过上述7个点中的任意两点所作的直线均属于平面ABCD。

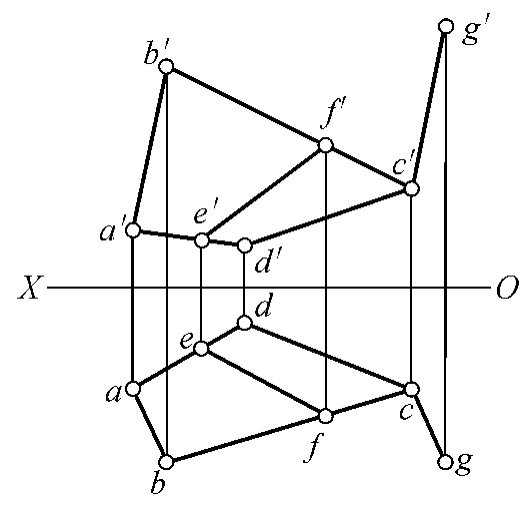
图5－6　点、直线属于平面的几何条件

【例5－1】　如图5－7（a）所示，已知平面ABCD及点E、F的二投影，判别点E、F是否属于平面ABCD。

解　（1）分析：根据上述条件，可假设点E属于平面ABCD，则过点E一定能任作一条直线属于平面ABCD（显然，若点E属于平面ABCD，则过点E能作无数多条直线属于该平面）；反之，点E不属于该平面。用同样的判定方法可判定点F是否属于平面。

（2）作图步骤如下。

第一步，判别点E是否属于平面ABCD，如图5－7（b）所示。

①连接b′e′并延长使其与c′d′相交于g′（这一步假设点E在直线BG上，由于BG属于平面ABCD，则点E在平面ABCD上）。

②过g′作OX的垂线交cd于g，连接bg。

③图5－7（b）的水平投影可知，直线BG属于平面ABCD，而点E不属于BG，所以点E不属于平面ABCD。

第二步，判别点F是否属于平面ABCD，如图5－7（c）所示。

①连接af交bc于h（这一步假设点F在直线AH上，由于AH属于平面ABCD，则点F在平面ABCD上）。

②连接点a′、f′，直线a′f′交b′c′于h′，连接h′和h。

③由于h′和h的连线垂直于投影轴OX，所以点H为直线AF和BC的交点，点H是平面ABCD上的点，点F为直线AH延长线上的点，则点F也为平面ABCD上的点。

图5－7　判断点E、F是否属于平面

从本题的解题过程可见，作图的第一步先从哪个投影图开始都无所谓（判断点E时，先从正面投影图作图，而判断点F时，先从水平投影图作图），关键是要选择合适的辅助线，如图5－7中的直线BG和AH。当然，辅助线不是唯一的，读者可自行试着换辅助线和作图方法，但不管怎么作，最终结论都是一样的。

思考：判断点E时，若先从水平投影图作图，应如何做？同理，判断点F时，若先从正面投影图作图，又如何做？自己做一做，看结论是否和例题一样。

【例5－2】　如图5－8（a）所示，已知平面ABC的正面投影中有个大写字母“T”，试完成大写字母“T”的水平投影。

解　（1）分析：大写字母“T”在平面ABC内，即组成该字母的两条直线段属于平面ABC，所以本题的关键是作组成字母“T”的两条直线段的水平投影。

（2）作图步骤如下。

①延长组成字母“T”的正面投影的两条直线段，使之与直线a′b′、a′c′、b′c′相交于d′、e′、f′、g′。

②分别过点d′、e′、f′、g′作OX轴的垂线交ab、ac、bc于d、e、f、g，并连接de和fg，如图5－8（b）所示。

③由于字母“T”的各点都在直线DE和FG上，故只需根据直线上点的投影特征，把组成字母“T”的各线段端点的水平投影绘出并连线即可完成作图，如图5－8（b）所示。

图5－8　求“T”字的水平投影

5.3.2　特殊位置平面上的点和直线的投影

由于特殊位置平面至少有一个积聚投影（投影面平行面有一个积聚投影，投影面垂直面有两个积聚投影），故特殊位置平面上的点和直线的检验和作图，常常借助积聚投影的特征。

特殊位置平面的积聚投影常表示为P^H、Q^V、R^W，其中P、Q、R表示平面的名称，上标H、V、W表示平面P、Q、R所垂直的投影面，例如P^H表示平面P垂直于H投影面的投影，即铅垂面（或正平面或侧平面）的H面积聚投影。特殊位置的非积聚投影如无必要可以不画，如果要画则仍应采用对应的小写字母（或小写字母加一撇或两撇）表示。

特殊位置平面内的点、线或平面图形在平面所垂直的投影面上的投影必落在该平面的积聚投影上；反之，如果点、线或平面图形的投影落在某平面的同面积聚投影上，则该点、线或平面图形必属于该特殊位置平面，如图5－9所示。

图5－9　特殊位置平面的积聚投影

【例5－3】　如图5－10（a）所示，已知点D、E是铅垂面ABC上的点，试完成D、E的水平投影。

解　（1）分析：铅垂面ABC的H面投影具有积聚性，而点D、E是其上的点，因而点D、E的H面投影必属于铅垂面ABC的H面积聚投影。

（2）作图步骤：分别过点d′、e′作OX轴的垂线并与铅垂面ABC的H面积聚投影abc相交，交点即为d、e，如图5－10（b）所示。

图5－10　求铅垂面上点的H面投影

【例5－4】　如图5－11（a）所示，已知直线段IJ是水平面FGH上的直线，试完成直线IJ的正面投影。

图5－11　求水平面上线段的V面投影

解　（1）分析：水平面FGH的V面投影具有积聚性，而直线段IJ是其上的线，因而IJ的V面投影必属于水平面FGH的V面积聚投影。

（2）作图步骤：分别过点i、j作OX轴的垂线与水平面FGH的V面积聚投影f′g′h′相交，交点即为i′、j′，直线段i′j′即为所求，如图5－11（b）所示。

5.3.3　平面内的投影面平行线和最大斜度线

在5.2节中，我们已经知道投影面垂直面对三个投影面的倾角有一个为90°，另外两个倾角的实形为积聚投影与相应投影轴的夹角；而投影面平行面对三个投影面的倾角一个为0°、另外两个为90°。但一般位置平面的三个投影与投影轴的夹角都不反映平面对投影面倾角的实形，为求解一般位置平面对投影面倾角的实形，必须寻找其他途径来解决。本节将探讨一般位置平面与投影面的倾角α、β、γ的图解方法。作为预备知识，首先需掌握平面内的投影面平行线和最大斜度线的概念、几何意义及作图方法。

1.平面内的投影面平行线

平面内的投影面平行线是指属于平面且平行于某一个投影面的直线。从定义可知，平面内的投影面平行线，既是平面内的直线，又是投影面的平行线，因此它既有平面内直线的投影特征，又有投影面平行线的投影特征。

如图5－12所示，对一般位置平面△ABC而言，它与任意高度的水平面H₁相交将会产生一条交线，该交线必是水平线。当若干个不同高度的水平面与一般位置平面相交时，均会产生这样的水平线。这种水平线属于一般位置平面△ABC，因而称为平面上的水平线。

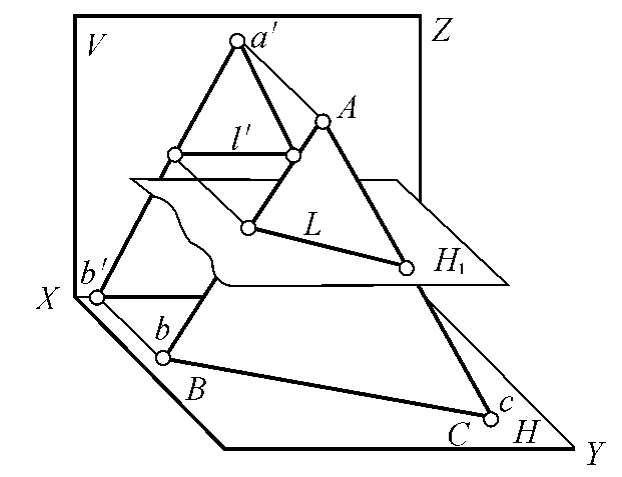
图5－12　平面上的投影面平行线形成示意图

根据直线所平行的投影面的不同，平面内的投影面平行线可分为以下三种。

①平面内的水平线：属于平面且平行于H面的直线。

②平面内的正平线：属于平面且平行于V面的直线。

③平面内的侧平线：属于平面且平行于W面的直线。

不难看出，在图5－13中，直线AD、AE、CF分别为平面ABC内的水平线、正平线、侧平线。

图5－13　平面内的各种投影面平行线

若要作平面上的投影面平行线，则先要作出其平行于投影轴的投影。如图5－13所示中，若要在平面上作水平线，首先要根据投影面平行线的投影特性，先作出水平线AD的正面投影面a′d′（a′d′∥OX轴），再根据属于平面的直线的投影特性，作出水平线AD的水平投影ad。同理，如要作出平面上的正平线，则需首先作出正平线AE的水平投影ae（ae∥OX轴），再根据属于平面的直线的投影特性，作出正平线AE的正面投影a′e′。

2.平面内对投影面的最大斜度线

平面内对投影面的最大斜度线是指属于平面且与某一投影面成最大倾角的直线。根据投影面的不同，最大斜度线有下列三种情况：

①平面内对H面的最大斜度线；

②平面内对V面的最大斜度线；

③平面内对W面的最大斜度线。

结合立体几何相关知识可知，平面内对某投影面的最大斜度线只能是平面内与相应迹线垂直的直线。如图5－14所示，平面P的水平迹线为DD₁，点C是平面P内的点，即直线CD、CD₁属于平面P，由于CD⊥DD₁，所以直线CD是平面P内对H面的最大斜度线。不难看出，平面P内对H面的最大斜度线CD与H面的夹角α就是平面P与H面的夹角。

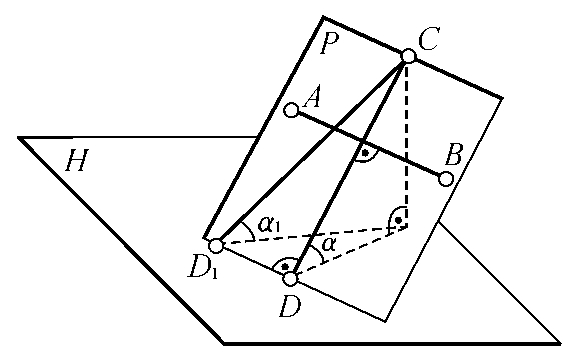
图5－14　平面P内对H面的最大斜度线

由于直线CD₁不垂直于DD₁，所以直线CD₁不是平面P内对H面的最大斜度线，故恒有α＞α₁。如果在平面P内取一直线AB，且使AB∥DD₁，显然AB是平面P内的水平线，则有CD⊥AB。同理可知，某个平面内对V、W面的最大斜度线具有类似的特点，因此也可以这样来定义三种最大斜度线。

①平面内对H面的最大斜度线：属于平面且与平面内的水平线垂直的直线。

②平面内对V面的最大斜度线：属于平面且与平面内的正平线垂直的直线。

③平面内对W面的最大斜度线：属于平面且与平面内的侧平线垂直的直线。

易知，平面内的投影面平行线和平面内对投影面的最大斜度线均为该平面内的一组平行线（有无数条），平面的迹线可以看作是平面内投影面平行线的特殊情形，例如图5－14中DD1可看作平面P内的一条水平线。

【例5－5】　如图5－15（a）所示，已知平面ABC的三面投影，求平面ABC对三个投影面的倾角α、β、γ。

解　（1）分析：由本节知识可知，要想求一般位置平面与某投影面的倾角，首先应该在该平面内找一条对该投影面的最大斜度线，然后求出这条最大斜度线与投影面的倾角，此倾角即为该平面对相应投影面的倾角。而要求平面内对某投影面的最大斜度线，则应先在该平面内找一条该投影面的平行线，利用平面内对投影面的最大斜度线与该投影面的平行线相互垂直的关系即可得解。

（2）作图步骤如下。

①求平面ABC对H面的倾角α，如图5－15（b）所示。

a.在平面ABC内作一条水平线。过点a′作OX轴的平行线线交b′c′于d′，利用直线上点的投影规律求出点D的另外两个投影d、d″，连接ad和a″d″。

b.作平面ABC内的一条对H面的最大斜度线JK。过直线ac上的任意一点j作直线ad垂线交直线ab于点k，利用直线上点的投影规律求出点J、K的另外两个投影，连接j′k′和j″k″，直线JK即为平面ABC内的一条对H面的最大斜度线。

c.利用直角三角形法求出直线JK对H面的倾角α的实形，α即为平面ABC与H面的倾角。在V（或W）面投影图上量取J、K两点沿OZ轴方向的坐标差ΔZ_JK，以ΔZ_JK长度作为直角三角形的一直角边，另一直角边的长度为JK的H投影长jk；则此直角三角形的斜边长度即为直线JK的实长，斜边JK与直角边jk的夹角即为角α的实形。

②求平面ABC对V投影面的倾角β，如图5－15（c）所示。

a.在平面ABC内作一条正平线。过点a作OX轴的平行线交bc于e，利用直线上点的投影规律求出点E的另外两个投影e′、e″，连接a′e′和a″e″。

b.作平面ABC内的一条对V面的最大斜度线CM。过点c′作直线a′e′的垂线交直线a′b′于点m′，利用直线上点的投影规律求出点M的另外两个投影，连接cm和c″m″，直线CM即为平面ABC内的一条对V面的最大斜度线。

图5－15　求作平面对三投影面的倾角α、β、γ

c.利用直角三角形法求出直线CM对V面的倾角β的实形，β同时也是平面ABC与V面的倾角。在W（或H）面投影图上量取C、M两点沿OY轴方向的坐标差ΔY_CM，以ΔY_CM长度作为直角三角形的一直角边，另一直角边的长度为CM的V投影长c′m′；则此直角三角形的斜边长度即为直线CM的实长，斜边CM与直角边c′m′的夹角即为β角的实形。

③求平面ABC对W面的倾角γ，如图5－15（d）所示。

a.在平面ABC内作一条侧平线。过点c′作OZ轴的平行线线交a′b′于f′，利用直线上点的投影规律求出点F的另外两个投影f、f″，连接cf和c″f″。

b.作平面ABC内的一条对W面的最大斜度线AN。过点a″作直线c″f″的垂线交直线b″c″于点n″，利用直线上点的投影规律求出点N的另外两个投影，连接an和a′n′，直线AN即为平面ABC内的一条对W面的最大斜度线。

c.利用直角三角形法求出直线AN对W面的倾角γ的实形，γ同时也是平面ABC与W面的倾角。在V（或H）面投影图上量取A、N两点沿OX轴方向的坐标差ΔX_AN，以ΔX_AN长度作为直角三角形的一直角边，另一直角边的长度为AN的W投影长a″n″；则此直角三角形的斜边长度即为直线AN的实长，斜边AN与直角边a″n″的夹角即为γ角的实形。