单元的数学描述和积分

5.3.1　单元的数学描述和积分

对一个悬臂梁进行静态分析，如图5.9所示，探究单元阶数（线性或二次）、单元数学描述和积分水平对结构模拟精度的影响。

梁长150mm、宽2.5mm、高5mm；一端固定，在自由端施加5N的集中载荷。材料的杨氏模量E为70GPa，泊松比为0.0。采用梁的理论，在载荷P作用下，梁自由端的挠度为

其中

式中　l——梁的长度；

　　　b——梁的宽度；

　　　d——梁的高度。

图5.9　自由段受集中载荷P的悬臂梁

当P＝5N时，自由端挠度是3.09mm。

1）完全积分（Full integration）

所谓“完全积分”是指当单元具有规则形状时，所用的高斯积分点的数目足以对单元刚度矩阵中的多项式进行精确积分。对六面体和四边形单元而言，所谓“规则形状”是指单元的边是直线并且边与边相交成直角，在任何边中的结点都位于边的中点上。完全积分的线性单元在每一个方向上采用两个积分点。因此，三维单元C3D8在单元中采用2×2×2个积分点。完全积分的二次单元（仅存在于ABAQUS/Standard）在每一个方向上采用3个积分点。对于二维四边形单元，完全积分的积分点位置如图5.10所示。

图5.10　完全积分时二维四边形单元中的积分点

应用ABAQUS/Standard模拟悬臂梁问题，采用了几种不同的有限元网格，如图5.11所示。采用线性或者二次的完全积分单元进行模拟，以说明两种单元的阶数（一阶与二阶）和网格密度对结果精度的影响。

图5.11　悬臂梁模拟所采用的网格

各种模拟情况下的自由端位移与梁理论解的比值，如表5.3所示。

表5.3　采用积分单元的梁挠度比值

应用线性单元CPS4和C3D8所得到的挠度值相当差，以至于其结果不可用。网格越粗糙，结果的精度越差，但是即使网格划分得相当细（8×24），得到的自由端位移仍然只有理论值的56％。需要注意的是，对于线性完全积分单元，在梁厚度方向的单元数目并不影响计算结果。自由端的误差是由于剪力自锁（Shear locking）引起的，这是存在于所有完全积分、一阶实体单元中的问题。

剪力自锁引起单元在纯弯曲时过于刚硬。可以解释如下：考虑承受纯弯曲结构中的一小块材料，如图5.12所示。材料产生弯曲、变形前平行于水平轴的直线成为常曲率的曲线，而沿厚度方向的直线仍保持为直线，水平线与竖直线之间的夹角保持为90°。

图5.12　在弯矩M作用下材料的变形

线性单元的边不能弯曲，所以，如果应用单一单元来模拟这一小块材料，其变形后的形状如图5.13所示。

图5.13　在弯矩M作用下完全积分、线性单元的变形

上述图中示出了通过积分点的虚线。显然，上部虚线的长度增加，说明1方向的应力（σ₁₁）是拉伸的。类似地，下部虚线的长度缩短，说明σ₁₁是压缩的。竖直方向虚线的长度没有改变（假设位移是很小的），因此，所有积分点上的σ₂₂为零。所有这些都与受纯弯曲的小块材料应力的预期状态是一致的。但是，在每一个积分点处，竖直线与水平线之间的夹角开始为90°，变形后却改变了，说明这些点上的剪应力σ₁₂不为零。显然，这是不正确的：在纯弯曲时，这一小块材料中的剪应力应该为零。

产生这种伪剪应力的原因是由于单元的边不能弯曲，它的出现意味着应变能正在产生剪切变形，而不是产生所希望的弯曲变形，因此总的挠度变小，即单元是过于刚硬的。

剪力自锁仅影响受弯曲载荷完全积分的线性单元的行为。在受轴向或剪切载荷时，这些单元的功能表现良好。而二次单元的边界可以弯曲（图5.14），故它没有剪力自锁的问题。从表5.3可见，二次单元预测的自由端位移接近于理论解答。但是，如果二次单元发生扭曲或弯曲应力有梯度，将有可能出现某种程度的自锁，这两种情况在实际问题中是可能发生的。

图5.14　在弯矩M作用下完全积分、二次单元的位移

只有确信载荷只会在模型中产生很小的弯曲时，才可以采用完全积分的线性单元。如果对载荷产生的变形类型有所怀疑，则应采用不同类型的单元。在复杂应力状态下，完全积分的二次单元也有可能发生自锁，因此，如果在模型中应用这类单元，应仔细检查计算结果。然而，对于模拟局部应力集中的区域，应用这类单元是非常有用的。

2）减缩积分（Reduced integration）

只有四边形和六面体单元才能采用减缩积分方法，而所有的楔形体、四面体和三角形实体单元，虽然它们与减缩积分的六面体或四边形单元可以在同一网格中使用，但却只能采用完全积分。

减缩积分单元比完全积分单元在每个方向上少用一个积分点。减缩积分的线性单元只在单元的中心有一个积分点（实际上，在ABAQUS中这些一阶单元采用了更精确的均匀应变公式，即计算了单元应变分量的平均值）。减缩积分单元在其名字中含有字母“R”。

对于减缩积分的四边形单元，积分点的位置如图5.15所示。

图5.15　采用减缩积分的二维单元的积分点

应用前面用到的4种单元的减缩积分形式和在图5.11所示的4种有限元网格，采用ABAQUS对悬臂梁问题进行了模拟，其结果列于表5.4中。

表5.4　采用减缩积分单元的梁挠度比值

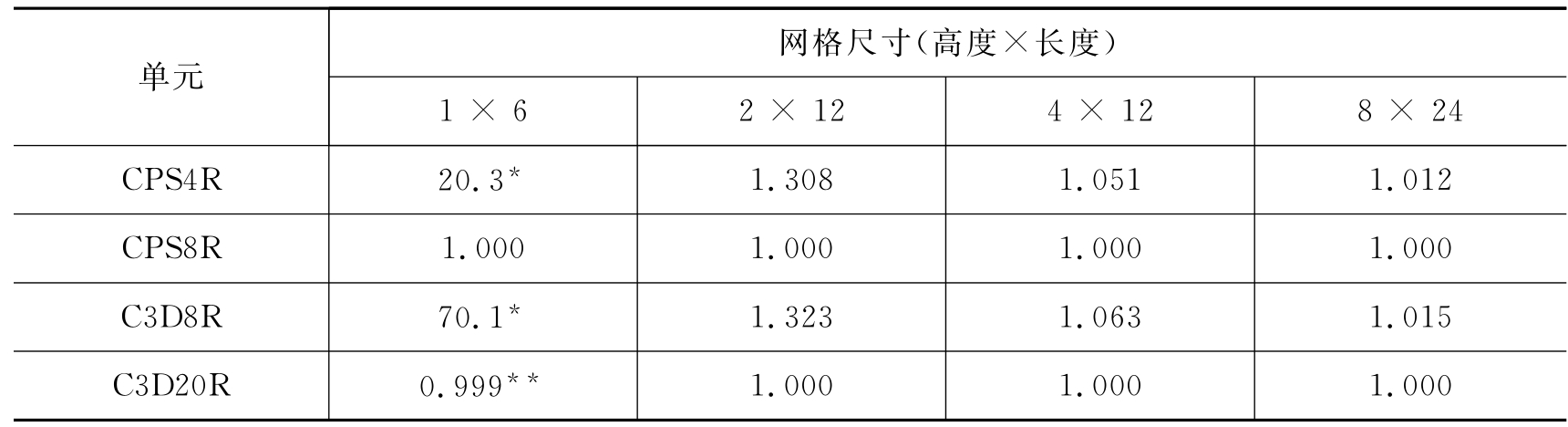
注：＊没有刚度抵抗所加载荷；＊＊在宽度方向使用了两个单元。

线性的减缩积分单元由于存在着来自本身的所谓沙漏（Hourglassing）数值问题而过于柔软。为了说明这一问题，再次考虑用单一减缩积分单元模拟受纯弯曲载荷的一小块材料（图5.16）。

图5.16　在弯矩M作用下减缩积分线性单元的变形

单元中虚线的长度没有改变，它们之间的夹角也没有改变，这意味着在单元单个积分点上的所有应力分量均为零。由于单元变形没有产生应变能，因此这种变形的弯曲模式是一个零能量模式。由于单元在此模式下没有刚度，所以单元不能抵抗这种形式的变形。在粗划网格中，这种零能量模式会通过网格扩展，从而产生无意义的结果。

ABAQUS在一阶减缩积分单元中引入了一个小量的人工“沙漏刚度”以限制沙漏模式的扩展。在模型中应用的单元越多，这种刚度对沙漏模式的限制越有效，这说明只要合理地采用细划的网格，线性减缩积分单元可以给出可接受的结果。对多数问题而言，采用线性减缩积分单元的细划网格所产生的误差（表5.4）在一个可接受的范围之内。建议当采用这类单元模拟承受弯曲载荷的任何结构时，沿厚度方向上至少应采用4个单元。当沿梁的厚度方向采用单一线性减缩积分单元时，所有的积分点都位于中性轴上，该模型是不能抵抗弯曲载荷的（这种情况在表5.4中用“＊”标出）。

提示：在ABAQUS的网格（Mesh）模块中，在单元类型（Element Type）对话框中，可以对线性减缩积分单元进行沙漏刚度控制（Hourglass control），如图5.17所示。

图5.17　线性减缩积分单元的沙漏控制

线性减缩积分单元能够很好地承受扭曲变形，因此在任何扭曲变形很大的模拟中可以采用网格细划的这类单元。

在ABAQUS/Standard中，二次减缩积分单元也有沙漏模式。然而，在正常的网格中这种模式几乎不能扩展，并且在网格足够加密时也不会产生什么问题。由于沙漏，除非在梁的宽度上布置两个单元，C3D20R单元的1×6网格不收敛，但是，即便在宽度方向上只采用一个单元，更细划的网格却收敛了。即使在复杂应力状态下，二次减缩积分单元对自锁也不敏感。因此，除了包含大应变的大位移模拟和某些类型的接触分析之外，这些单元一般是最普遍的应力/位移模拟的最佳选择。

3）非协调单元（Incompatible mode elements）

仅在ABAQUS/Standard中有非协调模式单元，它的主要目的是克服完全积分、一阶单元中的剪力自锁问题，在其名字中含有字母“I”。由于剪力自锁是单元的位移场不能模拟与弯曲相关的变形而引起的，所以在一阶单元中引入了一个增强单元变形梯度的附加自由度。这种对变形梯度的增强允许一阶单元在单元域上对于变形梯度有一个线性变化，如图5.18（a）所示。标准的单元数学公式使单元中的变形梯度为一个常数，如图5.18（b）所示，从而导致与剪力自锁相关的非零剪切应力。

图5.18　变形梯度的变化

这些对变形梯度的增强弯曲是在一个单元的内部，与位于单元边界上的结点无关。与直接增强位移场的非协调模式公式不同，在ABAQUS/Standard中采用的数学公式不会导致沿着两个单元交界处的材料重叠或者开洞，如图5.19所示。因此，在ABAQUS/Standard中应用的数学公式很容易扩展到非线性、有限应变的模拟，而这对于应用增强位移场单元是不容易处理的。

图5.19　在应用增强位移场而不是增强变形梯度的非协调单元之间可能的运动非协调性（ABAQUS/Standard中的非协调模式单元采用了增强变形梯度公式）

在弯曲问题中，非协调模式单元可能产生与二次单元相当的结果，但是计算成本却明显降低。然而，它们对单元的扭曲很敏感。图5.20用故意扭曲的非协调模式单元来模拟悬臂梁：一种情况采用“平行”扭曲，另一种采用“交错”扭曲。

图5.20　非协调模式单元的扭曲网格

对于悬臂梁模型，图5.21绘出了自由端位移相对于单元扭曲水平的曲线，比较了3种在ABAQUS/Standard中的平面应力单元：完全积分的线性单元、减缩积分的二次单元以及线性非协调模式单元。与预想完全一致，各种情况下完全积分的线性单元得到很差的结果。另一方面，减缩积分的二次单元获得了很好的结果，直到单元扭曲得很严重时其结果才会恶化。

当非协调单元是矩形时，即使在悬臂梁厚度方向上网格只有一个单元，给出的结果与理论值也十分接近。但是，即便是很低水平的交错扭曲也使得单元过于刚硬。平行扭曲也降低了单元的精度，只不过降低的程度相对小一些。

图5.21　平行和交错扭曲对非协调模式单元的影响

如果应用得当，非协调模式单元是非常有用的，它们可以以很低的成本获得较高精度的结果。但是，必须小心地确保单元扭曲是非常小的，当为复杂的集合体划分网格时，这可能是难以保证的。因此，在模拟这种几何体时，必须再次考虑应用减缩积分的二次单元，因为它们显示出对网格扭曲的不敏感性。然而，对于网格严重扭曲的情况，简单地改变单元类型一般不会产生精确的结果。网格扭曲必须尽可能地最小化，以改进结构的精度。

4）杂交单元（Hybrid elements）

在ABAQUS/Standard中，对于每一种实体单元都有相应的杂交单元，包括所有的减缩积分和非协调模式单元。在ABAQUS/Explicit中没有杂交单元，使用杂交公式的单元在其名字中含有字母“H”。

当材料行为是不可压缩（泊松比＝0.5）或非常接近于不可压缩（泊松比＞0.475）时，采用杂交单元。橡胶就是一种典型的具有不可压缩性质的材料。不能用常规单元来模拟不可压缩材料的响应（除了平面应力情况），因为在此时单元中的压应力是不确定的。

如果材料是不可压缩的，其体积在载荷作用下并不改变。因此，压应力不能由结点位移计算。这样，对于具有不可压缩材料性质的任何单元，一个纯位移的数学公式是不适宜的。

杂交单元包含一个可直接确定单元压应力的附加自由度。结点位移只用来计算偏（剪切）应变和偏应力。

5）单元汇总

上述4类单元的特点和使用场合，如表5.5所示。

表5.5　各种单元的特点及使用场合

续表5.5