中位数和众数描述数据的集中趋势

单变量描述分析_社会调查与统计

第一节　单变量描述分析

一、集中趋势分析(位置分析)

在社会调查中，我们总希望能找到一个典型的变量来代表全体变量，用一个统计指标来代表一系列数据，表示现象的一般水平。这种以一个统计指标或代表值来反映一组数据在具体条件下的一般水平的分析方法就是集中趋势分析法。这个表明事物的某一数量方面在具体条件下的一般水平的统计指标或代表值就叫集中趋势统计量或集中量数。常见的集中趋势统计量有平均数、中位数、众数、分位数等。

1.平均数(Mean)

平均数(Mean)也称算术平均数、均数、均值，它是人们最熟悉，使用最频繁的一个集中量数，是衡量数据的中心位置的重要指标，常用字母M或x表示。计算平均数的条件是，所有的数据必须是定距或定比测量层次的数据。

●简单算术平均数

在统计原始资料时，当资料是未分组资料时，计算简单算术平均数，其公式为:

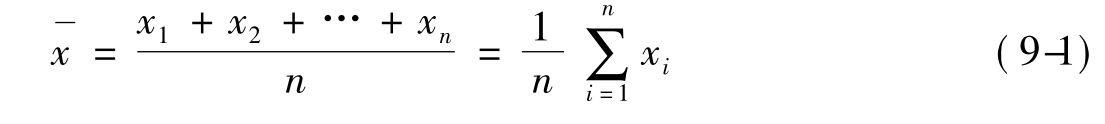
其中，x_i为各观测的结果，即观测值或实际调查数据，n为观测的次数。

例1　调查10个人的年龄分别是25岁、31岁、33岁、33岁、29岁、41岁、43岁、47岁、51岁、51岁，求他们的平均年龄。

因为是未分组资料，运用公式得:

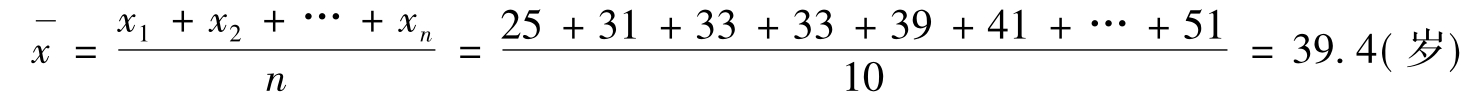
●加权算术平均数

研究者出于对分析的需要，常常将数据分成若干个组或者若干个类。这时数据是以次数分布表的形式出现的，当资料以单值表为分组时，一般地，其平均数的计算公式为:

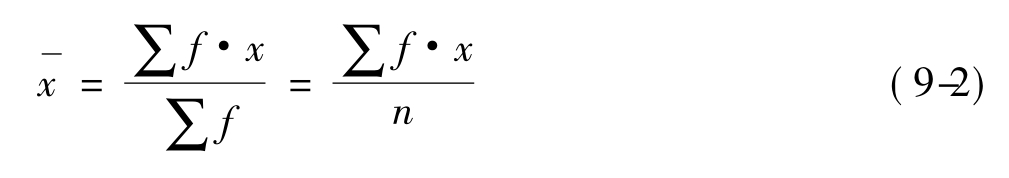
其中，公式中的f为各组的次数，∑f=n。

例2　表9-1是一个关于家庭人口的小型调查结果，求户均人口数。

表9-1　家庭人口的统计表

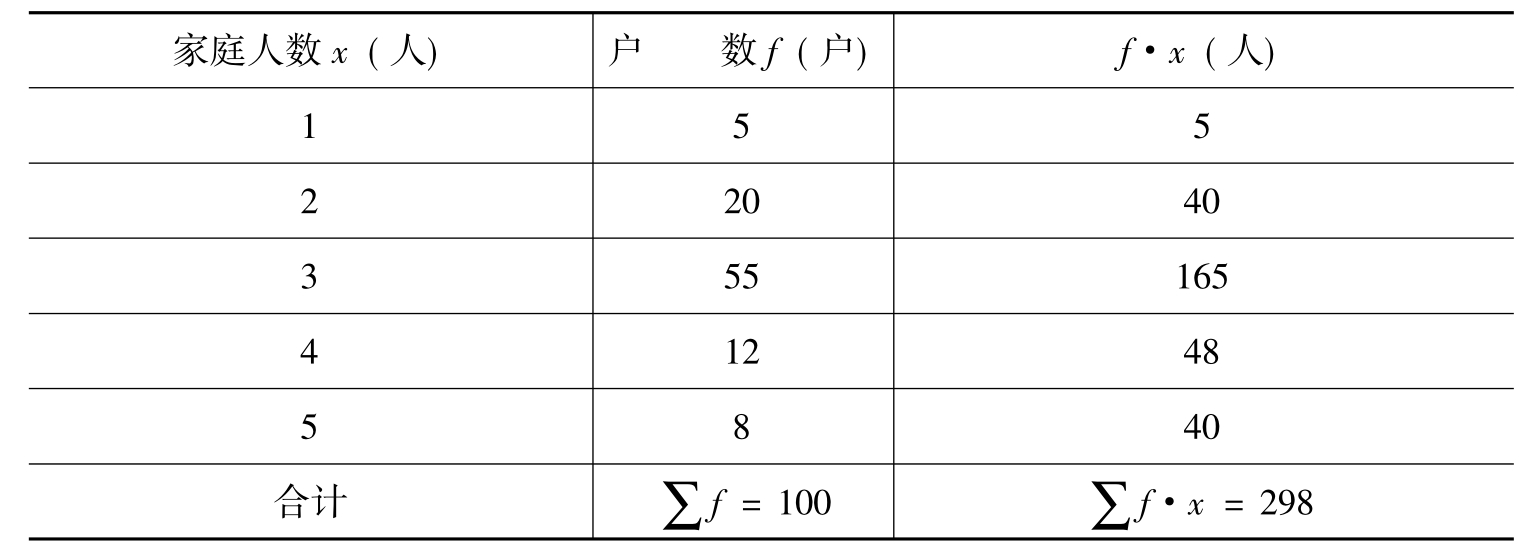
根据上述公式可得:

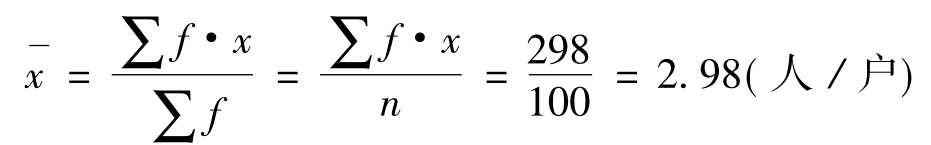
当资料以组距为分组时，一般地，其平均数的计算公式为:

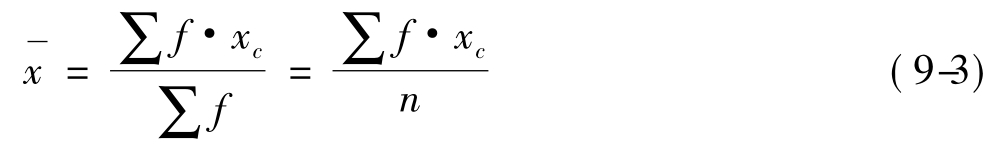
其中:x_c为各组的组中值(组中上限与组中下限的平均值)。

例3　表9-2是某单位收入的调查结果，请计算平均收入。

表9-2　收入的调查结果表

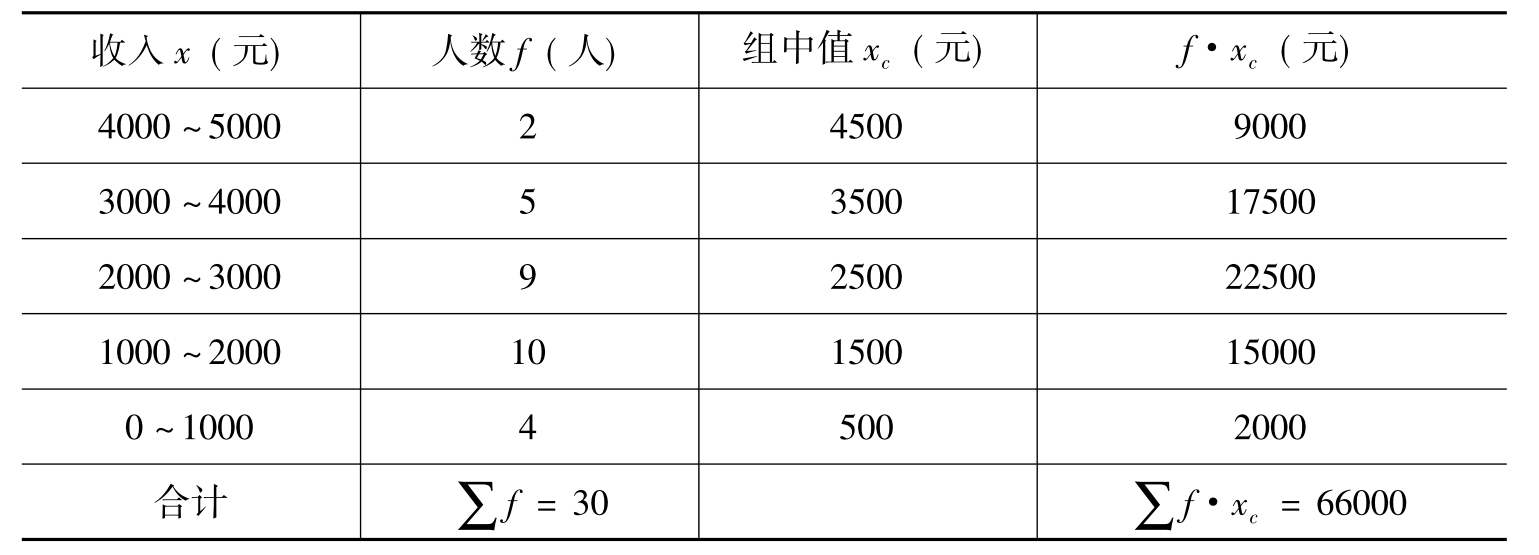
根据分组资料计算平均数公式可得:

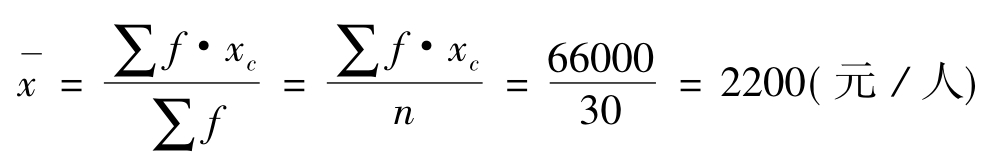
在具体计算平均数过程中，其本质上都是全部“数值”之和除以全部“次数”之和。

2.中位数(Median)

中位数又称中数、中点数，它是指一组数据在按大小顺序排列的情况下，位于中间位置上的那个数值，常用M_d表示。中位数的概念表明，它把观测总数一分为二，在其两边各有一半相同个数的数值，其中一半具有比它小的变量值，另一半具有比它大的变量值。当观测总数为奇数时，中位数是按顺序排列的位于正中间的数值。当观测数为偶数时，则中位数是最中间的两个数值的平均值。计算中位数的条件是，只有定序、定距、定比数据才能求中位数，定类数据则无中位数可言。

●对原始资料求中位数

中位数的计算方法:一般地，当观测数有n个时，首先对数据进行排序，由小到大，最小的数据的序号为1，最大的数据序号为n。

当n为奇数时，中位数序号为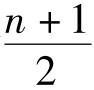的数值。即:

例4　求72，81，86，69，57，62这组数的中位数。

先将这些数字由小到大进行排列:57，62，69，72，81，86。由于观测数n=6为偶数，所以选取第3号位置和第4号位置的两个数字:69和72，则中位数为:(69+72)/2=70.5

从上面的例子可以看出，中位数仅与数据的排列位置有关，某些数据的变动对它的中位数没有影响。

●对分组资料求中位数

对于分组资料求中位数，首先按排序的方法找出中位数组，再按下面的公式(9-6)近似求得中位数:

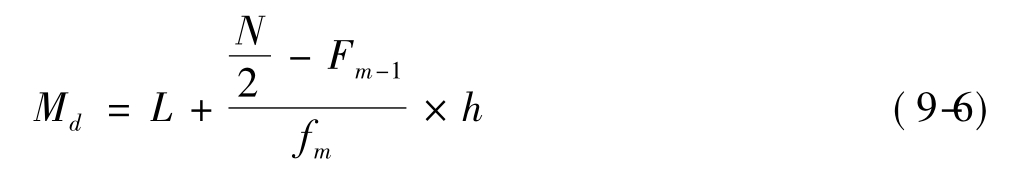
其中:L代表中位数组的下限，

N代表总体单位数，

F_m－1代表低于中位数组下限的累积频数，

f_m代表中位数组的频数，

h代表中位数组的组距。

例5　求表9-2中收入的中位数。

因为是分组的数据资料，可以得到中位数组为:2000～3000，中位数组下限L=2000，总体单位数N=30，中位数组下限的累积频数F_m－1为0～1000和1000～2000的累积频数为14即4+10，中位数组的频数f_m=9，中位数组的组距h=1000即3000－2000。运用公式得:

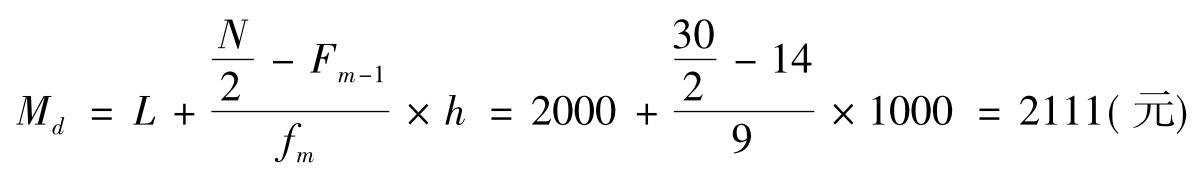
当然，若按次序由大到小，则计算的方向恰好相反，计算结果完全一样，其计算公式为:

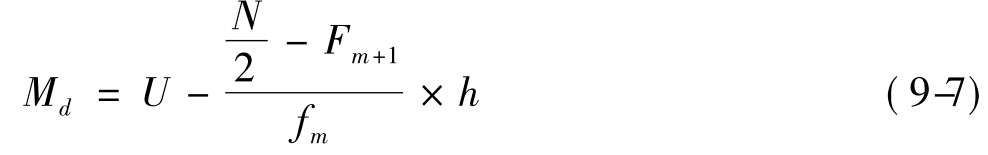
式中的U代表中位数组下限，F_m+1代表高于中位数组上限的累积频数，其余与上述公式一致。读者可以自己验证。

3.众数(Mode)

众数又称范数、密集数、通常数等，它是一组观测值中出现次数最多或出现频率最高的那个数的数值，常用符号M_o表示。众数也是一个比较常用的集中趋势统计量。它只与数值出现的次数有关，因而它可以用于定距资料，也可以用于定类、定序资料。在某些特殊情况下，众数有时不存在，有时可能出现多个。

●对原始资料求众数

对原始资料求众数，一般情况下只需要观察数据出现次数的分布情况即可。

例6　求72、81、56、81、92、86、57、81的众数。

按照众数的定义，很容易知道众数为81。

●对分组资料求众数

对分组式资料求众数的方法，是先根据数据出现的最高频数找出众分组，再按下面的公式(9-8)近似求得众数:

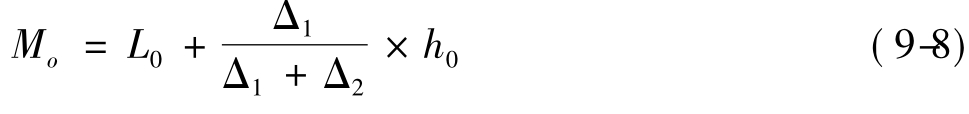
其中:L₀为众分组的下限，

Δ₁为众分组频数与前一组频数之差，Δ₂为众分组频数与后一组频数之差，h₀为众分组的组距。

例7　求表9-2中收入的众数。

由观察可知:最高频数的组为1000～2000，因此此组为众分组，且众分组的下限L₀=1000。众分组频数与前一组频数之差Δ₁=10－4=6，众分组频数与后一组频数之差Δ₂=10－9=1，众分组的组距h₀=1000，根据公式可以求得:

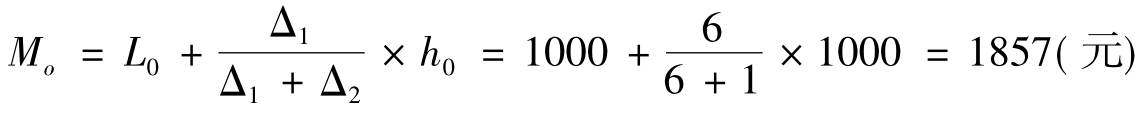
4.分位数(Quartiles)

分位数在对于详细研究总体时用处较大，包括百分位数，十分位数，四分位数，等等。分位数是中位数的推广。将一组数据从大到小按顺序排列起来，并计算相应的累计百分位，某一百分位所对应的数据的值就叫这一百分位的百分位数，最小值x₍₁₎是第0百分位数，最大值x_(n)是第100百分位数，中位数是第50百分位数。第25分位数又称为四分位数(下四分位数)，第75分位数也称为四分位数(上四分位数)。很明显，下四分位数是中位数以下数值的中位数，上四分位数是中位数以上数值的中位数。

5.平均数、中位数、众数的比较

平均数、中位数和众数三值设计的目的是共同的，都是希望通过一个数值来描述整体数据资料特征，以便简化资料。它们都是反映了变量的集中趋势。一般来说，众数:适用于定类、定序和定距变量；中位数:适用于定序和定距变量；平均数适用于定距变量。三者在反映变量的集中趋势时，各有优点，同时也存在一定的缺陷。

平均数对数据的利用率最高，它可以从无序的数据中直接求出；全部数据参与计算，因而具有高度的数学灵敏性和充分的代表性；其计算可由数学方程式加以确定，运算的结果可以成为其他统计运算的基础，可供进一步统计分析用。其主要缺点是由于每个数据都加入运算，容易受极端数值的影响，使平均数反映整体集中趋势变得面目全非。例如，某街道有20户居民，其中19户年平均收入为2万元，另一户为私营企业主，年收入达2000万元，由于这个极端数据的影响，街道每户年平均收入变成了101.9万元。很明显，该平均数所反映的集中趋势极不准确，这种影响在整体数据较少的情况下表现得比较明显。

中位数不受数据中极端数值的影响，因而，当一组数据中有特别大或特别小的数据，影响平均数的代表性时，选用中位数作代表比较合适。而且，在两极端数值不明确的情况下，仍可求出中位数，因为中位数需要知道的是正中间那个数据的值，其余的数据只是占据位置。但是中位数对数据的利用率极低，数学敏感性差，不便于作进一步的代数运算。

众数与中位数相似，不受极端值的影响，在偏态分布的情况下最能体现现象的集中趋势；众数还能在算术平均数和中位数都无法计算的定类测量尺度中运用，一组数据中不同类别的次数如果相差悬殊，众数则可以成为反映这组数据的较好的指标。缺点是受次数和分组的影响，稳定性差，在数据分布出现双峰时没有意义，且无法进行代数运算。^[3]

二、离中趋势分析(变异分析)

集中趋势统计量以一个数代表一个组，反映数据整体的平均水平和典型情况，但是，仅凭借集中趋势分析是很难准确地描述一组数据或者数据整体的。假设图9-1是某公司研发部和销售部的员工收入情况。

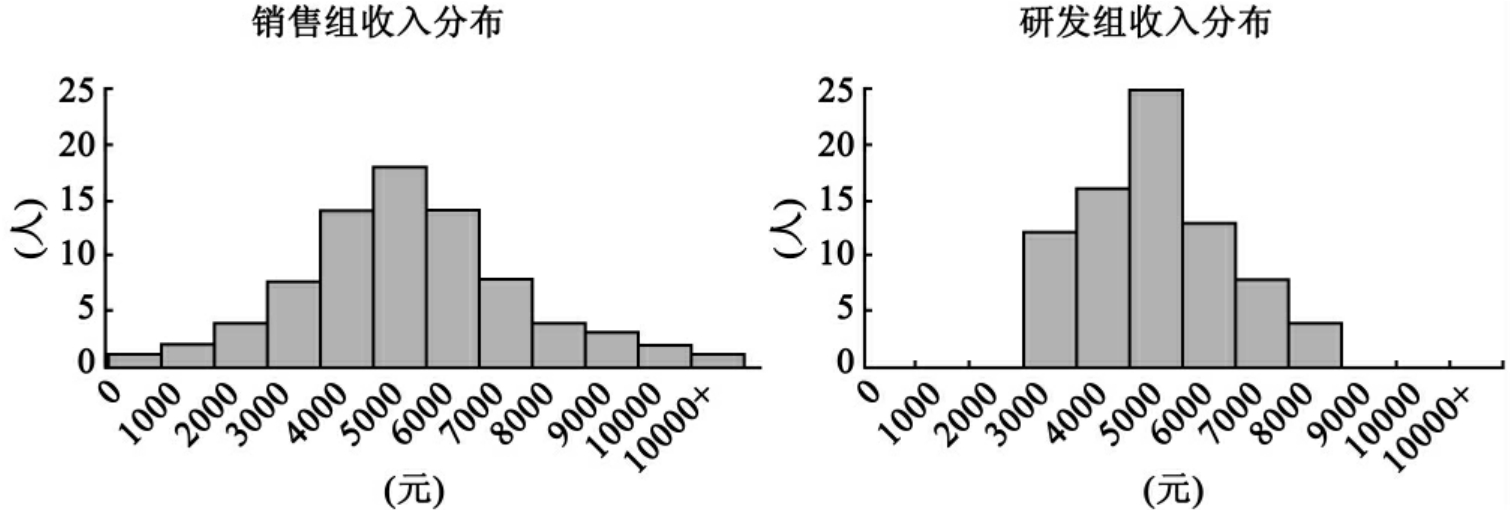
图9-1　某公司的销售部和研发部收入分布图

如果仅用集中趋势统计量来分析两个部门的工资收入水平，似乎两个部门的工资水平是相等的，但是两个部门的员工收入分布情况显然有很大的差别。研发部员工收入都差不多，在5000元上下波动，但是数据波动不大，销售部的平均收入虽然也是5000元，但是相差悬殊较大，数据非常分散。可见，仅用集中趋势来分析资料是不够的，还需要考虑资料的分散特征，既离中趋势。

所谓离中趋势，是指各数据之间的差距和离散程度，用离中趋势统计量来描述。离中趋势统计量，也叫离散量数、差异量数，就是表示一组数据变异程度或分散程度的量数。离中趋势统计量越大，说明数据分布越分散，那么该组数据的集中趋势统计量的代表性也越差；反之，离中趋势统计量越小，说明数据分布越集中，那么该组数据的集中趋势统计量的代表性也越好。集中趋势统计量指量尺上的一点，离中趋势统计量指量尺上的一段距离。我们只有把两者相结合才能更加清晰地了解一组数据的特点。

常用的离中趋势统计量主要有方差、标准差、变异系数、全距、异众比率、四分位间距等。

1.方差(Variance)与标准差(Standard Deviation)

方差是用来描述一组数据的波动大小，反映数据离中趋势的一个很重要的统计指标。方差是实际值与期望值之差的平方的平均值，它的计算方法是，把一组数据中每个数据与该组的平均数相减，将其差进行平方后相加，再除以数据的个数。其总体计算公式为:

其中:μ表示总体平均数。

在实际操作过程中，如果总体数目太大，则一般使用样本方差的计算公式，即:

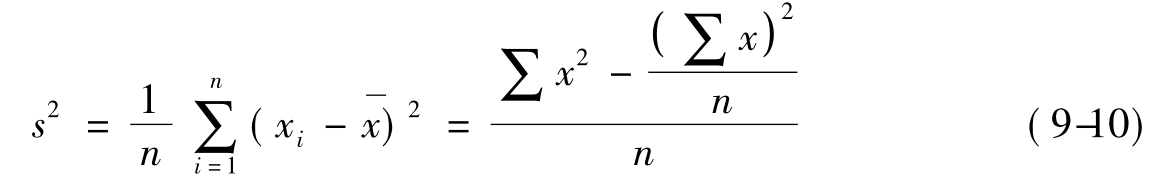
标准差其实质是方差的平方根，由于计算方差时，每个数据与平均数的差有正有负，所以要平方使之都变成正数后才不至于相互抵消。把数据与平均数之差，即(x_i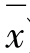－)平方后，数据的单位也被平方了，为了使离中趋势统计量的单位与原始数据相一致，又需要开平方，这就产生了标准差。^[4]总体标准差用σ表示，样本标准差用s表示。

总体标准差的计算公式为:

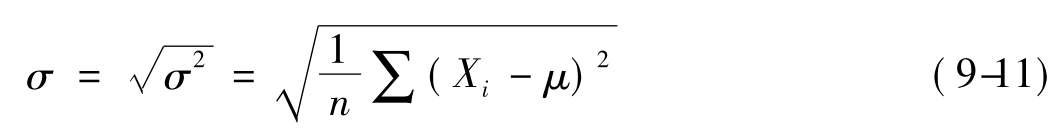
样本标准差的计算公式为:

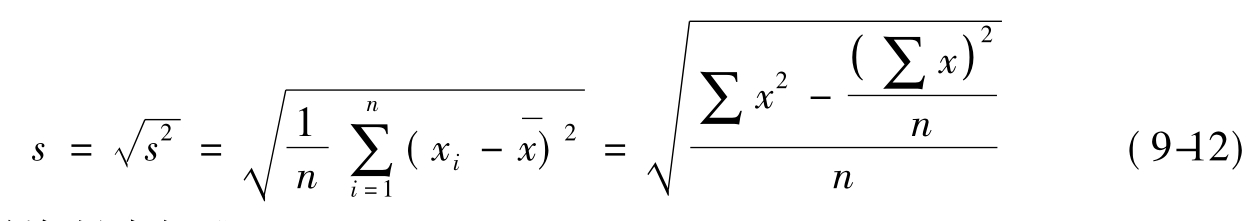
●对原始资料求标准差

对原始资料求标准差，直接按照上面的公式(9-11)、(9-12)即可求得。

例8　某校大一男生的入校外语成绩，在调查资料中随机拿出5个数据: 72、81、86、69、57(见表9-3)。求这组数据的标准差。

首先我们可以计算平均数: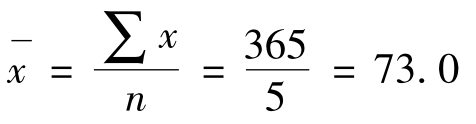

表9-3　原始资料数据求标准差的计算表

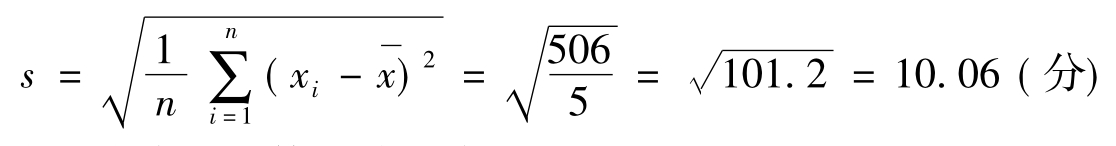
如果按照公式的另外一种形式:

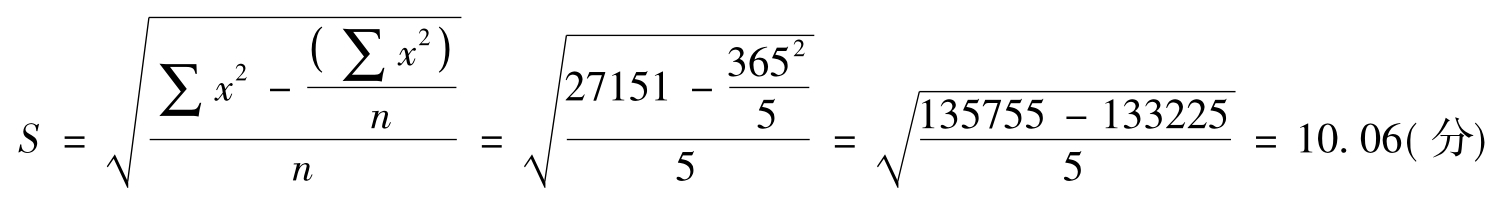
●对分组资料求标准差

对于分组资料，处理方法与前面的类似，其计算公式为:

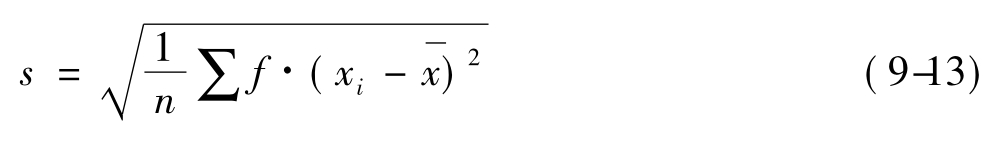
其中x_i为分组资料的组中值，∑f=n。

例9　某校大一男生的身高情况如表9-4所示，求他们的身高的标准差。

表9-4　分组资料数据求标准差的计算表

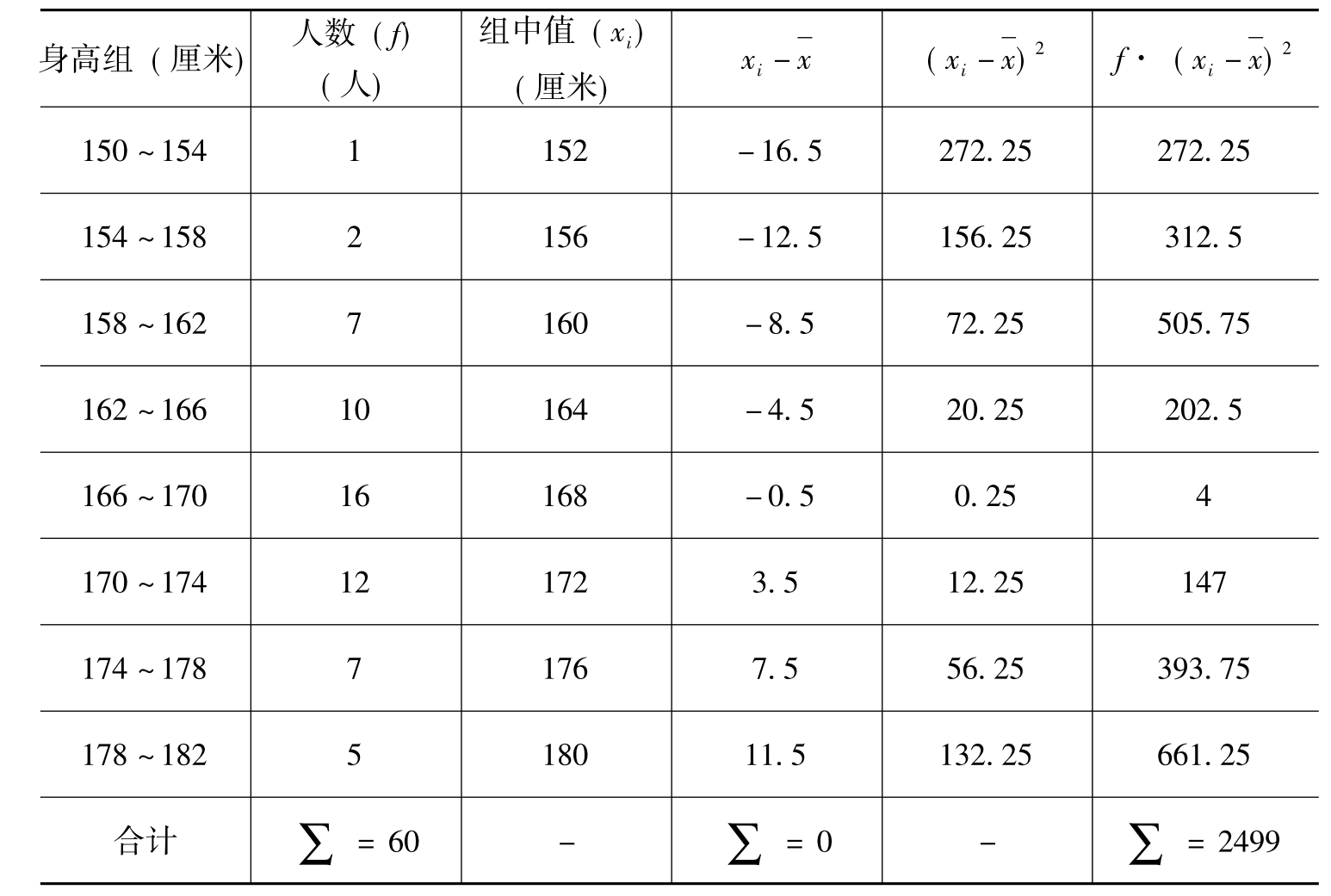
注:已知平均身高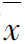=168.5

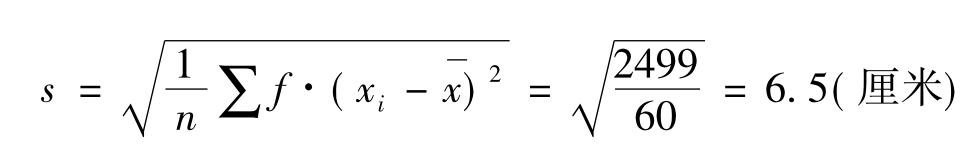
2.离散系数(Coefficient of Variance)

离散系数，也叫变异系数，是以相对数的形式表示的变异指标。为了对比分析不同水平的观测值之间的变异程度，就必须消除水平高低的影响，这时就要计算变异系数，它是标准差与平均数的百分比值，用CV表示，其计算公式为:

其中:CV表示离散系数，s表示样本标准差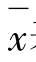，表示平均数。

例10　求例8中数据的离散系数。

离散系数是一个相对值，没有单位，其大小同时受平均数与标准差的影响，在比较两个或两个样本变异程度时，离散系数不受平均数与标准差大小的限制。如果观测值同乘以一个常数，则样本的离散系数保持不变。离散系数越大，波动程度越大。

3.全距(Range)

全距也叫极差，样本全距是样本中的最大值和最小值之间的差值，是表示资料中各观测值变异程度大小最简便的统计量。全距只利用了资料中的最大值和最小值，并不能准确表达资料中各观测值的变异程度，比较粗略。当资料很多而又需要迅速对资料的变异程度作出判断时，可以利用全距这个统计量。其计算公式为:

Range=x_max－x_min　　　(9-15)

4.异众比率(Variation Ratio)

异众比率是非众数的频数与全部个案的比值，用VR表示，其含义是指众数所不能代表的其他数据(即非众数数据)在总数据中的比重。它可以用于定距资料，也可以用于定类、定序资料。其计算公式为:

其中:VR表示异众比率，n表示样本数量，f_mo表示众数的样本个数。

例11　求例6数据的异众比率。

由于该组数据共有8个，所以n=8，众数Mo为81，其次数f_mo=3。

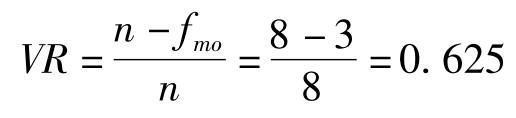
由此可以知道非众数占总数的一半以上。

VR值越大，表示非众数的个案所占总数据的比例越大，也就是众数的代表性越小；反之VR值越小，则表示众数的代表性越大。可见，异众比率这个离散趋势统计量是从反面检验众数的一项指标。

5.四分位差(Inter-Quartile Range)

四分位差也叫四分互差，或四分位间距，是指舍去一组数据的极端数据，而采用对数据的中央部分求全距的方法来测定离散程度的一种离散趋势统计量。样本四分位差即样本中的上四分位数(第三个四分位数)与下四分位数(第一个四分位数)之差，通常用字母IQR表示。四分位差主要适应于对定序及定序以上变量的分析，它的优点是可以克服全距中，极值对资料分散程度度量的干扰。其计算公式为:

IQR=Q₃－Q₁　　　(9-17)

其数据排列如图9-2所示。

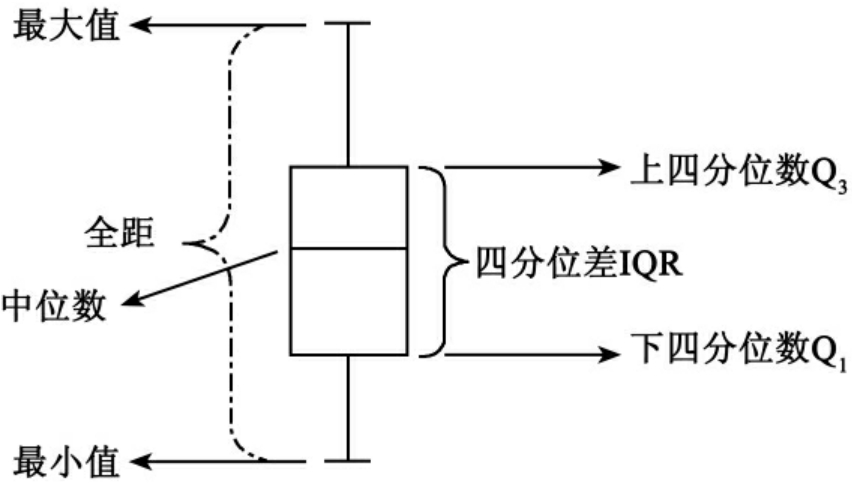
图9-2　数据排列箱形图

三、形状分析

在统计分析中，通常需要假设样本的分布属于正态分布，因此要用偏度和峰度两个指标来检查样本是否符合正态分布。

偏态(Skewness):主要考察数据的对称性。右偏态，又称正偏态:其偏态值大于0；左偏态，又称负偏态:其偏态值小于0。

峰态(Kurtosis):主要考察数据的分布尾部的拉长趋势。很多人认为是度量数据分布的陡峭性，其实这个说法不是很恰当。

偏度和峰度其实是用来衡量数据的总体分布与正态分布的偏离情况。理论上的正态分布偏度和峰度均为0。当两者太大时，需要作进一步检验和分析。此两个统计指标仅在对大样本分析时有效。考虑到本书的要求，这里没有给出其计算公式，有兴趣的读者可以参考其他统计学的书籍^[5]。

以上单变量描述统计都可以利用SPSS的分析(Analyze)菜单下的描述性统计(Descriptive-Statistics)中的(Frequencies)过程或者(Descriptives)过程完成，读者无须手工计算，只需将数据读入SPSS中，通过软件完成即可。