气体的一维等熵定常流动

本节将讨论气体等可压缩流体一维定常等熵流动。这是由于实际工程中，喷管、扩压管等管道内的可压缩流体在流动中，如果管道中心线的曲率不大，有效截面的形状和面积沿管道中心线的变化不大，则可以认为这些管道有效截面上的各点流动要素近似相等，则可以用有效截面上的平均流动要素代替有效截面上各点的流动要素。因此，再结合本章§9．1中的假定，用一维等熵定常流动来处理管道内的气体流动，既反映了流动的本质，又使流动的研究大大地简化。

9．3．1　气体一维定常流动的基本方程

1．连续性方程

在管道中任取一由相距dx的两个有效截面1—1、2—2和管壁组成的微元控制体，如图9-7所示。由第3章给出的一维定常可压缩流体的连续方程(3-45)

图9-7　连续性方程推导示意图

即对一维定常可压缩流体，通过流管的任意有效截面的质量流量Q为常数。对于积分形式的式(9-10)，两边取对数，得

lnρ+lnv+lnA=C

两边微分得

式(9-11)为连续性方程的微分形式。式(9-10)、式(9-11)为一维定常可压缩流体流动的基本方程。

2．运动方程

应用理想流体的运动方程(3-50)第一式

由于流动为一维定常流，质量力忽略，有ux=v，uy=uz=0，则可以写成

或

将上式沿流线积分，得

式(9-13)为一维定常可压缩流体流动的基本方程之一。只要知道了ρ、p的关系，就可求得式(9-13)的积分，进而求解该方程。

由式(9-12)可见，压强增量dp为正值时，速度增量dv为负值;反之亦然。也就是说，气流压强增大之处，则为流速减小之处;或者，气流压强减小之处，则为流速增大之处。

3．能量方程

由热力学第一定律即能量守恒定律

dq=du+

其中q为热量、u为内能、为体积。现引入焓h的表达式有h=u+，两边进行微分，可得

其中=。将上式代入式(9-12)，得vdv+dh－dq=0，移项可得用于流动的能量关系式

对于绝热流动，有dq=0，则有

进行积分可得能量方程的一种表达式

式(9-16)可以用于可逆或不可逆的绝热流动，也就是在熵增加的情况下也是正确的。

由物理学及热力学可知，对于完全气体，有

则式(9-16)可以写成完全气体的能量方程

注意到。由物理学及热力学可知，其中第一项有

即第一项为单位质量气体所具有的内能。因此，改写能量方程(9-16)

可以说明，能量方程(9-19)的物理意义为:在完全气体的一维定常流中，流管内任意有效截面(或流线上任一点)上的单位质量气体的内能u、压强势能和速度动能三项之和保持不变。

9．3．2　完全气体一维定常等熵流动的基本方程

根据前面的推导，下列方程

为一维定常理想可压缩流体(完全气体)流动的基本方程组。方程组有p、ρ、T、v4个未知数，共有四个方程，方程组是封闭的。

为计算式(9-13)中的积分，需要知道p与ρ的关系式。针对一维定常等熵流动，有等熵过程关系式=C(const)。对该式微分得

dp=Cγργ－1dρ

代入式(9-13)第一个积分，得

即

式(9-24)与能量方程式(9-22)完全相同。这就是说，在等熵的条件下，能量方程式(9-22)与运动方程式(9-13)完全一致。但是在非可逆的绝热过程条件下，或者说在非等熵的条件下，由运动方程式(9-13)是推导不出能量方程式(9-22)的。

这样，在等熵的条件下，能量方程与运动方程重合，其基本方程只有三个独立方程。为使基本方程封闭，需增加等熵过程方程式(9-4)。则有下列方程

为一维定常等熵流动的基本方程组，该方程组只能用于可逆的绝热流动。

9．3．3　气流的三种参考状态

根据前面的叙述，已知在求解一维定常等熵流动中某一有效截面上的未知流动参数时，需要知道流动中的另一个有效截面上的有关已知参数。对这个具有已知参数的有效截面，在前面方程推导时，并没有规定必须是什么截面。如果能找到一些参考截面，在该截面上的参数在整个流动过程中是不变的，则对一维定常等熵流动的计算和讨论将带来方便。这种参考截面上的参数，就是下面要讨论的气流参考状态。

1．滞止状态

如果在一维定常等熵流动中，对于气流速度不为零的某截面或某点的压强p、密度ρ和温度T等参数，可以称为静参数。如静压p、静温T等。如果当某截面或某点的气流速度等于零时，这个截面或这个点上的气流状态称为滞止状态。滞止状态下相应的参数称为滞止参数或总参数。如驻点处就是滞止状态，该处的参数为滞止参数。

对于一维定常等熵流动，滞止参数可以从流动中存在的滞止点得到，也可以通过设想气流速度等熵地滞止到零而得到。也就是说，滞止参数在一些流动中，可以是存在于流动中的，也可以是隐含在整个流动过程中的。因此可以作为一种参考状态的参数，在计算和分析中使用。

滞止参数以下标为“0”来表示，如p0，ρ0，T0，c0等。

对能量方程式(9-16)，并考虑式(9-17)、式(9-5)，有下列能量方程式

令v=0，得用滞止参数表示的常数

这样能量方程可以写成常数中含有滞止参数的方程，如

或

注意方程(9-30)，在滞止状态下，动能全部转变为其他的能量，这时候，h可以取最大值h0，称为总焓、驻点焓、滞止焓。方程(9-31)中T可以取最大值T0，称为滞止温度、总温，比气流的温度(静温)高。因此，测量温度时应注意，静止的温度计只能测出气流的总温。只有以气流速度相同速度运动的温度计才可以测出静温。

在滞止时的压强p0，称为总压，滞止压强。对应于滞止温度T0，有滞止音速c0=。这些都是常用的参考参数。

例9-2有一一维定常等熵气流，测得其中一截面上压强为p=1．67×105Pa，温度为T=25℃，速度为v=167m/s。试给出该气流的滞止压强、滞止温度和滞止密度。其中气体为空气，γ=1．4，R=287J/(kg·K)。

解已知温度T=25+273=298K。由能量方程(9-28)

由状态方程(9-27)和等熵过程关系式(9-4)得

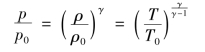
即

再由状态方程可得

2．极限状态

如果在一维定常等熵气流的某一截面上，气流的温度T=0，即焓h=0，则根据能量方程式(9-28)，在该截面上气流的速度可以达最大值vmax。这个最大值vmax称为最大速度或极限速度，这时的状态称为极限状态。也就是说在这个状态中，等熵气流随着气体的膨胀、加速，分子无规则运动的动能全部转换成宏观运动的动能，这时气流的静温和静压均降低到零，气流速度达到极限速度vmax。由式(9-29)、式(9-30)可得

由于实际气体在达到这个速度之前已经液化了，因此极限速度vmax仅仅具有理论上的意义。但由于极限速度vmax在等熵气流中不变，是个常数，因此常用做参考速度。另外由式(9-28)还可以得出下列极限速度vmax关系式

式(9-33)说明，沿流程单位质量气体所具有的总能量等于极限速度的速度动能。

3．临界状态

当一维定常等熵气流的某一截面上的速度等于当地音速时的状态称为临界状态。可以说临界状态是处于滞止状态和极限状态之间的一种状态。注意式(9-33)以及表示该式的图9-8中c～v曲线平面图，可以看出，当气流速度v被滞止到零时，当地音速c则上升到滞止音速c0;当地音速c下降到零时，气流速度v则被加速到极限速度vmax。因此，在气流速度v由小变大和当地音速c由大变小的过程中，必定会出现气流速度v恰好等于当地音速c的状态，即v=c或Ma=1的状态，即为临界状态。临界状态下的气流参数称为临界参数，出现临界状态的截面称为临界截面。临界状态用下标cr表示之。

图9-8　c～v曲线平面图

在临界状态下，vcr=ccr，由式(9-33)可得

或

可见，对于给定的气体，临界音速也只决定于总温，在绝热流中ccr是常数，在气体动力学中ccr是一个重要的参考速度。

应注意区别当地音速c与临界音速ccr:当地音速是指气体所处状态下实际存在的音速;而临界音速则是与气流所处状态相对应的临界状态下的音速。然而，当Ma=1时，当地音速便是临界音速。对于气体的某种实际流动状态，有与之相对应的滞止参数，也有与之相对应的临界参数。

9．3．4　一维定常等熵气流中各参数关系式

1．以马赫数Ma为变量的各参数关系式

从上述各参数关系式可见，只要知道气流的马赫数Ma和滞止参数，就可以求解一维定常等熵流动的T、p、ρ等流动参数。

2．速度系数M*为变量的各参数关系式

在分析气流各参数的关系时，还使用另一个无量纲参数，即表示气流速度与临界音速之比的速度系数，用M*表示，即

速度系数M*是与马赫数Ma相类似的另一个无量纲参数，两者有确定的对应关系。从式(9-34)解出c0，代入式(9-33)，两边同除以v2，可得

整理，可得

式(9-40)所表示的速度系数M*与马赫数Ma的关系曲线如图9-9所示。

另将式(9-42)代入式(9-36)～式(9-38)，可得速度系数表示的表达式

图9-9　M*与Ma的关系曲线

从上述各参数关系式可见，对于一维定常等熵流，速度系数的增大，气流的温度、音速、压强和密度都将降低。只要知道气流的速度系数M*和滞止参数，就可以求解一维定常等熵流动的T、p、ρ等流动参数。

引用速度系数的意义:

(1)应用速度系数M*计算气流速度v比应用马赫数Ma计算方便。

在等熵流动中临界音速ccr是个常数，根据速度系数的定义，在已知速度系数M*计算气流速度v时，只需用M*乘以常数ccr即可;而等熵流动中的当地音速c是随当时当地的气流参数T等变化的，在应用马赫数Ma计算气流速度v时，则要通过气流参数T求出当地音速c，然后才能求出气流速度v，比应用M*计算要麻烦许多。

(2)在极限状态中，马赫数Ma趋于无穷大，速度系数M*则为一常数。

在等熵流中，当气流速度v趋于极限速度vmax时，当地音速c趋于零，则Ma趋于无穷大，因而在极限状态附近无法利用马赫数为变量的参数关系式计算有关气流参数。该处如果利用速度系数M*为变量的参数关系式，则无上述困难，因为当v=vmax时，有

极限状态下的速度系数M*max为一有限量。例如对于γ=1．4的气体，M*max=2．4495。

(3)可以作为流动类型的判别标准

M*与Ma之间有确定的对应关系，如式(9-41)、式(9-42)，并参见图9-9，可得

当Ma=0时，M*=0，不可压缩流;

当Ma＜1时，M*＜1，亚音速流;

当Ma=1时，M*=1，音速流;

当Ma＞1时，M*＞1，超音速流。

3．临界参数与滞止参数的关系式

在以马赫数Ma为变量的参数关系式(9-36)～式(9-38)中，令式中的Ma=1，有

若＞0．6339，则为亚音速流;

若＜0．6339，则为超音速流。

例9-3气体在一无摩擦的渐缩管道中流动，已知截面1的压强为p1=2．67×105Pa，温度为T1=330K，流速为v1=157m/s，并且在管道出口截面2达到临界状态。试求气流在出口截面的压强、密度、温度和速度。假定气体为空气，γ=1．4，R=287J/(kg·K)。

解首先利用式(9-5)、式(9-36)和式(9-37)，计算截面1的音速、马赫数、滞止压强和滞止温度

然后利用式(9-47)、式(9-48)、式(9-5)以及状态方程计算截面2处于临界状态的临界压强、临界温度、临界密度以及临界流速。