统计质量控制的基本原理

第一节　统计质量控制的基本原理

一、质量波动及其统计规律

生产实践表明，在生产制造过程中，无论生产条件多么严格，生产环境多么理想，都无法加工出两个完全相同的零件，它们的特性值总是存在着差异。如用45号钢制造轴，经锻造成毛坯后，其化学成分在标准范围内或多或少总会有差异；毛坯进厂经过调质处理，其延伸率在标准范围内不会完全一致；加工过程中使用的机床、刀具和夹具的瞬时状态不可能完全不变；操作工人的技术和精神状态常会发生波动；加工后的轴会因检验人员和量具的变动而出现测量误差；此外，如温度、湿度、照明等环境因素的细微变化也会影响加工精度，从而使轴的质量特性产生差异。质量差异是生产制造过程的固有本性，质量的波动具有客观必然性。

生产过程质量控制的任务，是要把质量特性值控制在规定的波动范围内，使过程处于受控状态，能稳定地生产合格品。波动范围定得太大，产品质量得不到保证；但若盲目缩小波动控制范围，则会增加质量控制的难度和费用。一般来说，凡对产品输出特性影响大而控制成本低的零部件，可把允许波动范围规定得紧一些；而对产品输出特性影响小而控制成本高的零部件，可把允许波动范围规定得宽一些。

工序质量波动有多种表现形式，如产品和产品之间的差异，产品和质量标准之间的差别，不同批次产品质量之间的不一致性等。但从引起质量波动的原因来看，质量波动可分为偶然性波动和系统性波动两类。偶然性波动由大量的、微小的不可控因素的作用而引起，这种波动具有随机性。如材料成分的微小差异、机床的固有振动、刀具的正常磨损、工人操作技术上的细微变化等。偶然性波动对工序质量的影响比较小，在现有生产技术条件下也难以识别和消除。因此，偶然性波动也称为正常波动。工序质量控制的任务是使正常波动维持在适度的范围内。

系统性波动由少量的但较显著的可控因素的作用而引起，这种波动不具有随机性。如材料规格不符、设备故障、刀具的严重磨损、操作者违反操作规程等。系统性波动在未查明原因、采取纠正措施前始终具有系统性，往往导致生产过程的失控，对工序质量的影响十分显著，甚至是破坏性的。系统性波动也称为异常波动。系统性波动虽然常由突发性因素引起，但在现有生产技术条件下一般易于识别和消除。工序质量控制的任务是及时发现异常波动，查明原因，采取有效的技术组织措施消除系统性波动，使生产过程重新回到受控状态。

偶然性和系统性、正常和异常之间的关系是相对而言的。对微小的、不可控的随机性因素缺少有效的控制，常会累积成或诱发出系统性因素，导致异常波动，使生产过程失控。由于技术和管理的进步，使原来难以识别和消除的正常波动变得可以识别并消除。这时，原来的正常波动在新的生产技术条件下将被转化为异常波动。为了不断提高生产过程质量控制的水平，在有效控制正常波动，及时消除异常波动的基础上，应当通过质量改进，使一些不可控随机性因素逐渐成为可控的系统性因素，不断推进质量管理的水平。

生产制造质量是产品设计、工艺选择、计划调度、人员培训、工装设备、物资供应、计量检验、安全文明、人际关系、劳动纪律等工作在生产现场的综合反映，工序质量是诸多因素的综合作用。人们常将影响工序质量的因素归纳为“5M1E”，即操作者（man）、机器设备（machine）、材料（material）、工艺方法（method）、测试手段（measure）及环境条件（environment）。工序质量控制常表现为对“5M1E”这六大因素的控制。

在工序质量控制中，由于产品及工艺的不同，工序质量有时是产品质量特性，如尺寸、重量、精度、纯度、强度、额定电流或电压等；有时是工艺质量特性，如生产装置的温度、压力、浓度、时间等；有时也可表现为物耗或效率等。因此，工序质量波动的具体表现就是生产过程中这些质量特性的波动。

质量特性值的波动具有统计规律性。虽然，质量波动的个别观测结果具有随机性，但在受控状态下的大量观测结果必然呈现某种统计意义上的规律性。这种统计规律性是统计质量控制的必要前提和客观基础。

统计质量控制是统计质量管理中的一个重要问题。所谓统计质量控制，就是对生产过程中工序质量特性值总体进行随机抽样，通过所得样本对总体作出统计推断，采取相应对策，保持或恢复工序质量的受控状态。在统计质量控制中，工序质量特性值的观测数据是工序质量的表现，不仅反映了工序质量的波动性，也反映了这种波动的规律性。

根据质量特性值的属性，质量数据可分成计数值和计量值两种类型，其中计数值又可分为计件值和计点值两种。

计数值质量数据不能连续取值，如不合格数、疵点数、缺陷数等。对于计数值质量数据，若只能按“件”计数时，可称为计件值数据，如一批产品中的不合格品数等；若必须按“点”计数时，可称为计点值数据，如一块布上的疵点数或一个工件表面的缺陷数等。计数值类型的质量特性值的统计规律可用离散型随机变量来描述。在统计质量控制中常见的离散型随机变量有超几何分布、二项分布、泊松分布等。

计量值质量数据可以连续取值，如长度、容积、重量、浓度、温度、强度等。计量值类型的质量特性值的统计规律可以用连续型随机变量来描述。正态分布是统计质量控制中常见的连续型随机变量。

二、几个常用的随机变量

在质量控制中，常用的随机变量有超几何分布、二项分布、泊松分布和正态分布。下面分别介绍它们的概率分布、数字特征以及应用中的主要问题。

（一）超几何分布（hypergeometric distribution）

设有限总体由N个产品组成，其中有D个不合格品。对该总体作不放回随机抽样，样本容量为n。样本中不合格品数X为一离散型随机变量，服从超几何分布，其恰为d的概率。

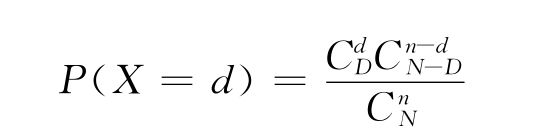
容易知道，d＝0，1，2，…，min（n，D）。数学期望和方差分别为

超几何分布随机变量源于有限总体的不放回抽样模型，适用于计件值型质量特性值的控制和检验问题。

例1　某批产品共40件，其中不合格品有12件。现从中任意取9件，以X表示其中不合格品的件数。求X的概率分布及其数字特征。

解：9件样品中不合格品的件数为超几何分布随机变量。

（二）二项分布（binomial probability distribution）

设无限总体不合格品率为p（合格品率q＝1－p）。对其作随机抽样，样本容量为n。样本中不合格品数X为一离散型随机变量，服从二项分布，其恰为d的概率。

其中，d＝0，1，2，…，n。

二项分布随机变量X的数学期望和方差分别为

EX＝np　DX＝np（1－p）

二项分布随机变量源于n重贝努利（Bernouli）试验或自某总体的n次还原抽样，适用于计件值型质量特性值的控制和检验问题。

例2　某种型号电子元件当其寿命超过3 000小时时为合格品。已知某一大批该产品的合格品率为0．2。现从中随机地抽查20只，求20只元件中恰有d只为合格品的概率。

解：本例属破坏性检验，当然是不放回抽样，但由于该批元件总数很大，抽样数量又很少，对总体的影响是微不足道的，故可作为无限总体放回抽样处理。因此，抽查的20只元件中的合格品数X可看作是二项分布随机变量，其恰为d的概率。

P（X＝d）＝Cd₂0（0．2）^d（0．8）^20－d d＝0，1，2，…，20

（三）泊松分布（Poisson distribution）

泊松分布是应用最广泛的随机分布之一，常用来描绘稀有事件计数资料的统计规律性。例如，在一定时间内（或一定空间中）各种稀有事件（如事故、灾害、疾病等）出现的次数，到达某服务机构（如电话交换台、修理部、车站、商场等）要求服务的顾客数，纺纱机上的断头数，布匹上的疵点数，产品表面的缺陷数，每页书上的印刷错误数，大地震后的余震数，放射源的放射性粒子数等等。泊松分布随机变量在计点值型质量特性值的控制和检验中有重要应用。

设离散型随机变量X服从泊松分布，则其取值k的概率

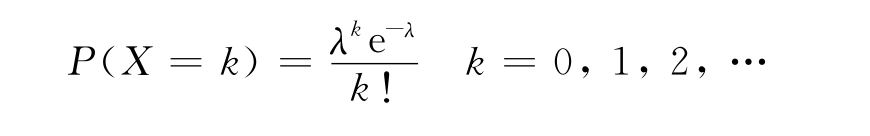
其中λ＝np，n为样本容量，p为不合格率（或缺陷率等）。容易知道，λ＝np实际上是样本中不合格品的平均数（或缺陷等的平均数）。

泊松分布随机变量X的数学期望和方差分别为

EX＝λ，DX＝λ

理论上泊松分布有可数无限个可能值，但随着k值的增大，P（X＝k）迅速变小，有实际意义的是为数有限的较小的几个k值。

例3　设临床统计资料表明，服用某种药剂产生副作用的概率为0．002。求在1 000例服用该药物的病人中，恰有k例出现副作用的概率。

解：因为样本容量n＝1 000，副作用发生率p＝0．002，所以，1 000例中发生副作用的病人数的数学期望λ＝np＝2。因此，1 000例服用此药的病人中发生副作用的人数X服从如下的泊松分布：

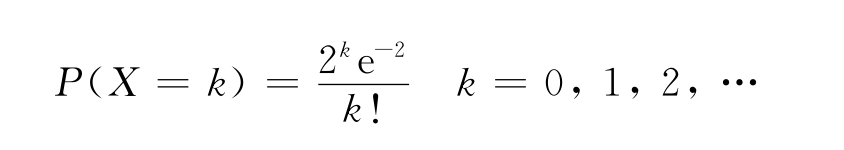
例4　某织物每百平方米平均有7个疵点。现抽检了5平方米这种织物，试求下列事件的概率：A＝｛无疵点｝，B＝｛恰好有一个疵点｝，C＝｛最多有一个疵点｝。

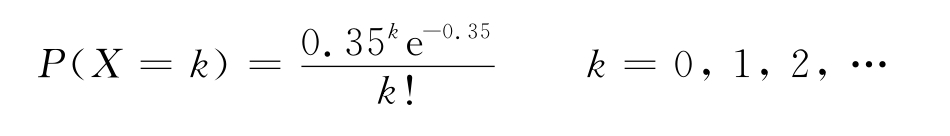
所以，所求各事件的概率依次为

P（A）＝P（X＝0）＝e^－0．35＝0．7047；

P（B）＝P（X＝1）＝0．35e^－0．35＝0．2466；

P（C）＝P（X≤1）＝P（X＝0）＋P（X＝1）＝0．9513。

虽然在理论上疵点数X可以有任意多个，但无疵点数或只有一个疵点的概率高达95%以上，而有两个或两个以上疵点的概率充其量不足5%。所以，一旦任意抽检5平方米该种织物后，如发现疵点数超过一个时，首先应当怀疑的是疵点率是否已上升，从而采取必要的检查和纠正措施。

（四）几种离散型概率分布之间的关系

超几何分布源于对有限总体的不放回（非还原）抽样。由于每次抽取的样品不再放回总体，故每次抽样结果将影响总体的不合格品率。因此，每次抽样的结果不是相互独立的。二项分布源于对无限总体的有限抽样。由于总体无限，每次抽取的样品无论是否返回总体，都不会影响总体的不合格品率。因此，每次抽样的结果是相互独立的。由于这个原因，二项分布也适用于有限总体的放回（还原）抽样。其实，在实际应用场合，总体的有限和无限、样本的大小及不合格品率的高低都是相对而言的，并无绝对的界限，在一定条件下，两种分布的适用性可以相互转化。

有关研究表明，当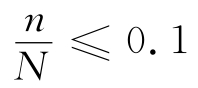（即样本容量相对总体较小）时，或当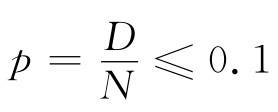（即总体不合格品率较低）时，可以用二项分布来近似超几何分布。当N较大时，二项分布的计算要比超几何分布的计算方便得多。

泊松分布描述稀有事件出现概率，或者说反映随机点（随机事件）在一定时间（空间）内的散布规律，和超几何分布及二项分布的产生背景有根本的区别。但是，当总体相当大（甚至无限），不合格品率又很低时，抽样中不合格品的出现将成为稀有事件，因而在一定条件下，超几何分布和二项分布可以用泊松分布来近似计算。

有关研究表明，当样本容量n较大，且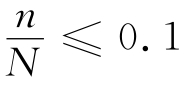及p≤0．1时，超几何分布可以用泊松分布来近似；当n较大（如n≥100），p较小（如p≤0．1），同时np≤4时，二项分布可以用泊松分布来近似。这种近似引起的误差并不影响实际的使用，但泊松分布的计算要比另两种分布的计算容易许多。

泊松分布是应用十分广泛的离散型随机变量，它和连续型正态分布随机变量有着密切的联系。有关研究表明，当样本中不合格品数平均值λ＝np≥5时，泊松分布以正态分布为极限分布，因此，可用正态分布近似。

（五）正态分布（normal distribution）

正态分布是应用最为广泛的一种连续型概率分布，在计量值型质量特性值的控制和检验中经常被用来描述（或近似描述）质量变化的规律。

1．正态分布随机变量的定义和性质

设连续型随机变量X的概率密度为

其中μ，σ＞0为常数，则称X服从参数为μ，σ的正态分布，记为X～N（μ，σ²）。

正态分布随机变量X的分布函数为

特别地，若参数μ＝0，σ＝1，即X～N（0，1），则称X为标准正态分布随机变量。

正态分布随机变量X的数学期望和方差分别为

EX＝μ，DX＝σ²

实际上，参数μ作为总体平均值，描述质量特性值分布的集中位置和对称中心，参数σ作为总体标准差，描述质量特性值分布的分散程度。正态分布质量特性值的分布曲线由μ和σ两者唯一确定。

2．正态分布的概率计算

习惯上，常将标准正态分布的密度函数记为φ（x），而将分布函数记为Φ（x），即

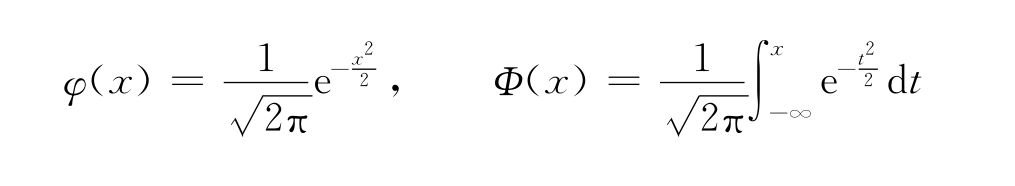
标准正态分布的密度函数值和分布函数值有表可查。

对于一般的正态分布，可先将其转化为标准正态分布，然后求相应的概率值。

因此，一般正态分布的概率计算公式为

例5　已知X～N（μ，σ²），求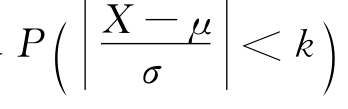，其中k＝1，2，3，4，5，6。

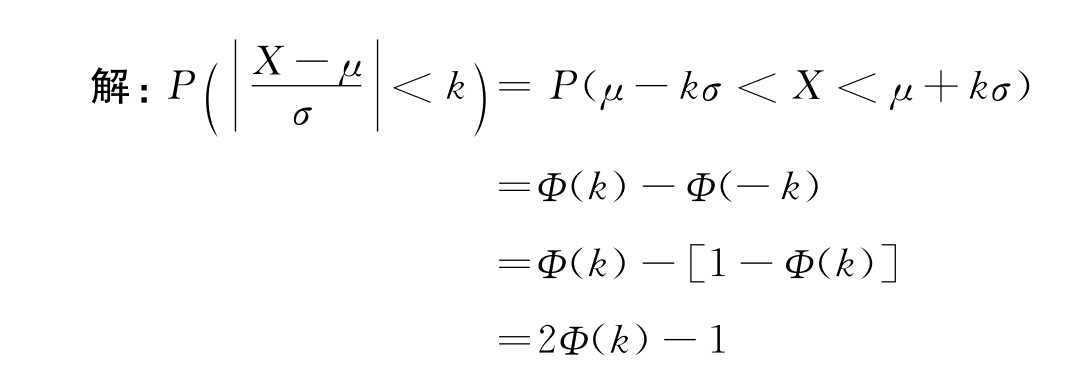
所以，所求概率依次为

在质量控制中，k＝3时的情形特别有用。它告诉我们，如果质量特性值X服从参数为μ和σ的正态分布，那么，它落在区间（μ－3σ，μ＋3σ）内的概率高达99．73%；相反，落在区间之外（即x＜μ－3σ或x＞μ＋3σ）的概率只有0．27%。这就是众所周知的“3σ”原理。根据“3σ”原理，如果发现质量特性值X的观测结果不在区间（μ－3σ，μ＋3σ）内，就有合乎逻辑的理由怀疑生产过程已经失控，面临的质量波动是由系统性的不良因素引起的。因为在这种情况下，生产过程仍然正常的可能性只有0．27%，而已失常的可能性却高达99．73%。

例6　某袋装食品重量服从正态分布，重量平均值为296克，标准差为25克。为了维护消费者利益，重量规格下限定为273克。求低于规格下限的不合格品率。

解：在实际问题中，质量特性值X的概率分布是未知的。根据概率论中心极限定理，如果质量特性值由大量偶然性因素共同作用而形成，并且每个因素的单独作用相对均匀地微小，那么质量特征值X的概率分布就近似于正态分布。退一步来说，即使原本并非正态分布的随机变量，其独立随机样本的平均值也以正态分布为极限分布。在本例中，每袋食品的重量在受控条件下受来自“5M1E”诸因素的影响，故可以认为重量X服从正态分布，并且其重量的样本平均值x＝296克和样本标准差s＝25克可以作为重量总体的数学期望μ和总体标准差σ的估计值。因此可以认为，本例中每袋食品的重量X～N（296，25²）。

本例中重量规格下限x_L＝273克，μ≈x＝296克，σ≈s＝25克。所求不合格品率p_L为图7－1中阴影部分的面积。因此，p_L＝P（X＜273）。

图7－1　产品重量超出下限的不合格品率

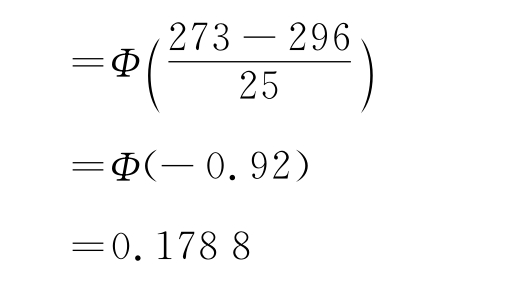
从计算结果来看，重量不足的不合格品率高达17．88%≈18%。

例7　在例6的基础上，假设重量的公差中心M＝x＝296克，重量规格上限x_U＝319克。现欲将p_L值降为0．01，试分别讨论重量分布中心μ应提高到多少或重量标准差σ应减少到多少。

解：先讨论分布中心μ的提高问题。示意图见图7－2。

图7－2　提高包装袋袋重的效果

设新的分布中心应提高到μ′。因

查正态分布表得

所以，μ′＝273＋2．33×25＝331．3克。

此时，重量超出规格上限的不合格品率p_U将上升。

因为　　　　　p_U＝P（X＞x_U）＝1－P（X≤x_U）

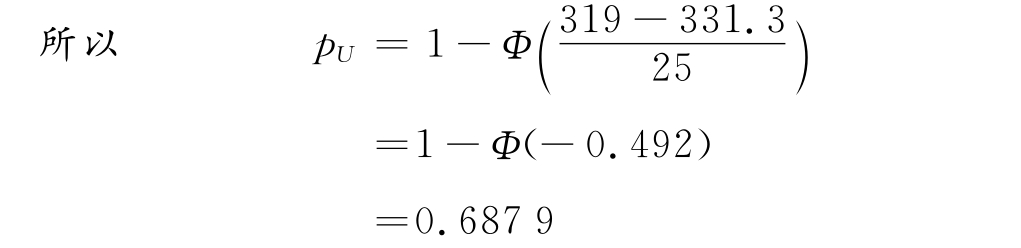
再讨论总体标准差的缩小问题。示意图见图7－3，设新的总体标准差应缩小到σ′。

图7－3　提高包装精度的效果

从本题计算结果来看，为了维护消费者利益，使p_L值下降到0．01，可以提高袋重的控制标准，将重量分布中心移到μ′＝331．3克，但p_U值将上升到0．687 9，企业利益将受到极大的损害；也可以缩小重量总体标准差，将重量波动的标准差控制在σ′＝9．86的水平上。由于分布中心和公差中心一致，故此时的p_U＝0．01，既维护了消费者的利益，又保障了企业的利益。但标准差的缩小，即重量控制精度的提高，有赖于技术上和管理上的投入。企业是否有能力这么做，或是否值得这么做，应综合各方面的因素才能决定。

例8　假设一大批产品的一等品率为20%。现在从中随机抽取100件，求其中一等品件数介于13和30之间的概率。

解：100件产品中一等品件数X是一个二项分布随机变量。由题知p＝0．2，q＝1－p＝0．8，n＝100。所以，100件产品中一等品件数介于13和30之间的概率

此概率虽然可以求出，但十分麻烦。和其他许多概率分布一样，二项分布的极限分布是正态分布，故在一定条件下，二项分布的概率计算可用正态分布来近似。

因为本例中EX＝np＝20，DX＝npq＝16，σ＝4。所以

即100件产品中，一等品数介于13和30之间的概率大约为0．953 7。