人们对眼光学的认识有一个逐渐深化的过程。最早发现使用正球镜可以解决阅读问题,之后发现负透镜可以帮助看远。发现散光以后,人们认识到人眼在不同的子午线上需要不同度数和符号的透镜。然而,当人们考虑到不规则散光时,这些问题就非常复杂了,简单的几何光学是根本无法解决的。
波前像差与光学系统结构参量(如透镜厚度、透镜表面曲率半径等)之间的关系极其复杂,不可能以具体的函数式表达出来,因而也无法采用解方程之类的办法直接由像差要求计算出系统的精确结构参量。现在所能做到的是求得满足初级像差要求的解。初级像差是实际像差的近似表示,仅在孔径和视场较小时才能反映实际的像差情况。
1.参考光轴 人眼系统常用的两个轴线均经过黄斑的中心凹,它们分别称为视轴和视线,后者经过瞳孔中心。在物体空间,视轴的定义为连接目标物体和眼第一结点的连线,而在像空间,视轴定义为连接第二结点和黄斑中心凹的连线。视线的定义为通过入瞳和出瞳中心并连接中心凹的间断连线。视线和中心凹主线的光路相同,并遵守光学标准,但少数人,其视轴和视线可能并不一致,因此对视网膜的成像质量会有一定的影响。
根据美国光学学会(Optical Society of America, OSA)的标准,选用视线作为测量和计算人眼光学像差的参考光轴(reference optical axis)。用此方法所计算的波前像差将以瞳孔中心为笛卡尔坐标系的原点。
2.光程差表示 从应用光学角度看,波前像差有多种表示方法。波前像差一般可用像差图和Zernike多项式来表达和分析。由于波前像差是实际波面和理想波面之间的光程差,因此使用计算光程的方法来计算波前像差比较方便。像差图分析是通过光线路径长度(optical path length, OPL)来解释的,OPL是指光线在穿过某一物体使其波长须振荡的次数,是由物理光径长度和屈光介质所决定的。光程是一个抽象的概念,借助于这个概念,可以将光在不同介质中所经历的路程长度折算为光在真空中以相同时间所经历的路程长度,以便于可用同一标准来比较不同介质中光传播状态的不同变化。
在理想眼中,从瞳孔各点的入射光线经过相同次数的振荡到达视网膜,形成一个理想的成像。但是由于实际的屈光介质会存在着各种的问题而会导致光学系统具有波前像差,那么其光线的路径长度之间就会存在着差异,各条光线的光程与经过瞳孔中心的主光线的光程的差值为光程差(optical path difference, OPD),也即为各光线的波前像差(图2-7)。

图2-7 人眼的波前像差ab和a’b
换句话说,当两个非相干光线通过两个不同光路时,两个光线之间的时间差转换成距离并乘以真空中光速的时间差就是这两条光线的光程差。计算公式为:
(t2-t1)c =(n-1)l (公式2-2)
在这里,n是透镜或介质的折射率,l为光程长度。
在图2-7中,瞳孔的中心点P,理想波前所在的瞳孔球面的中心是焦点f,波前像差函数w(x,y)是与理想波前和实际波前的距离成比例,对于图2-7中的折射光线,波前像差可以认为是ab或a’b,对于人眼光学系统,ab与a’b基本相等。鉴于约定,w(x,y)> 0就意味着波前比主光线相位提前,对于近视眼来说,光线传播的长度比主光线要短,两者的光程差小于零,其大小与相同位置(x,y)的波前像差相等,但符号相反,即
OPD(x,y)= - w(x,y) (公式2-3)
假如介质是不均匀的话,那么不同点的光程差相对于参考面来说就会不同,在空间中,我们就无法将所有这些点都连接成具有相同光程差的波前(图2-8)。
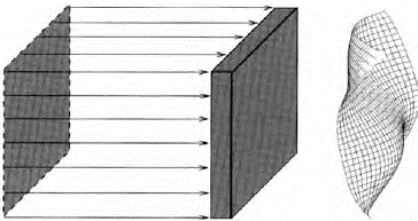
图2-8 平面波通过折射率不同的非均匀性介质传播时,在不同点上有相同的相位。对所有这些点的表面进行连接就形成了波前(引自:Guang-ming Dai:Wavefront Optics for Vision Correction)
3.Zernike多项式表示 见本章第四节波前像差的Zernike多相式。
4.傅立叶级数表示 见本章第五节波前像差的傅立叶级数表示法。
5.泰勒(Taylor)单项式表示 泰勒单项式是以英国科学家Brook Taylor命名的,他用级数来代表各种函数,广泛用于各种科学领域。
在笛卡儿坐标系中,泰勒单项式是以(x + y)n表达式的功率扩展。在泰勒单项式中对一个波前可以通过一系列单项式的方式来表示:

泰勒单项式在极坐标中的表示法为:
Tqp(ρ,θ)=ρpcosqθsinp-qθ (公式2-5)
这里,p是径向阶数,q为方位角频率。在笛卡儿坐标系中,泰勒单项式可以写成:
Tqp(x,y)=xqyp-q(公式2-6)
泰勒单项式通过p,q来表示其阶数,表2-1显示泰勒单项式在笛卡儿坐标系和极坐标系中前4阶的解析表示法。
表2-1 0到4阶的泰勒单项式

(摘自:Guang - ming Dai:Wavefront Optics for Vision Correction)
泰勒单项式的主要优点是简单并且是一组完整的基函数。由于它的完整性,所以我们可以通过泰勒单项式对图像的变形进行解析分析,图2-9为通过泰勒单项式对6阶像差的解析分析,图2-10则是通过泰勒单项式针对4阶像差的点扩散函数(PSFs)和20/20字母E的模糊图像。
但是,由于泰勒单项式不是正交归一的,因此它不如Zernike多项式和傅立叶转换那样能够比较好地用于表达眼的波前像差。
6.椭圆多项式表示 对于一个圆形瞳孔,使用Zernike多项式来表示眼的波前像差具有很好的优势。但是在实际工作中,绝大多数人眼的瞳孔并非圆形而是接近椭圆。当瞳孔为椭圆时,Zernike多项式就无法成为正交归一的,因此就会丧失其表示眼波前像差的优越性。对于椭圆,我们可以采用新的正交归一的多项式来表示,这就是椭圆多项式。
椭圆多项式的处理方法非常复杂,本文仅作一个基本的介绍。表2-2为0到3阶椭圆多项式,需要注意的是ε为椭圆的纵横比(图2-11)。
每个椭圆多项式有不同的椭圆系数,当椭圆系数相同时,纵横比ε越小,则图像的变形就越大(图2-12)。由于椭圆瞳孔的短轴为垂直轴,因此在垂直方向上所有的PSFs被垂直拉长了。

图2-9 0到6阶泰勒单项式的形状
(引自:Guang-ming Dai:Wavefront Optics for Vision Correction)

图2-10 各种泰勒单项式
(从上到下分别为T4,T5,T8,T9,T12,T13和T14)的PSFs和20/20字母E的有效模糊图像,它的泰勒系数分别为(A)0.5μm, (B)1μm,(C)2μm。每个图像的视场大约为5’× 5’
(引自:Guang-ming Dai:Wavefront Optics for Vision Correction)

图2-11 3到9阶椭圆多项式的形状
ε=0.8(引自:Guangming Dai:Wavefront Optics for Vision Correction)
表2-2 0到3阶的椭圆多项式

当纵横比ε→1时,它们就变成了Zernike多项式(引自:Guang-ming Dai: Wavefront Optics for Vision Correction)

图2-12 各种椭圆多项式(从上到下分别为E3,E4,E5,E6,E7和E8)的PSFs和20/20字母E的有效模糊图像,它的椭圆系数为0.1μm,瞳孔的长轴为6 mm,纵横比ε分别为(A)0.25,(B)0.5,(C)0.75。每个图像的视场大约为5’× 5’
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














