策略：反复、模进
旋律的模进是一种特殊的重复手法，在不同高度上重复旋律。
这里借用音乐中的这一术语，通过了解、反复、递进，来增强学生对某种数学思想或方法的理解、体验与感受。
教学片段1：
了解环节：
借助于“思考①、②、③”揭示几何与代数的对应关系。
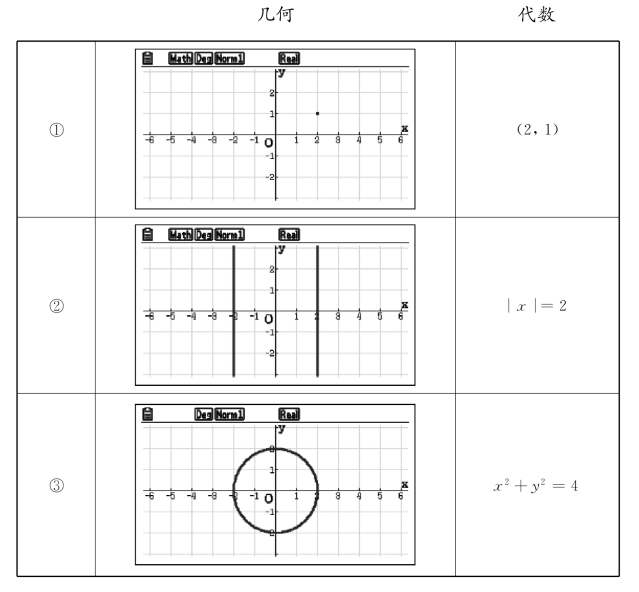
对思考①，先给出直角坐标平面内的一个点，强调它是一个几何对象，再问该几何对象所对应的代数对象是什么。
对思考②和③，先分别给出代数对象|x|＝2和x2＋y2＝4，让学生说出在平面直角坐标系中它们所对应的几何对象是什么。
思考：
设计说明：
设计这样三个思考，目的强调几何与代数的对应关系，了解什么是解析几何。
思考①，从几何对象到代数对象；思考②和③，从代数对象到几何对象。这样，正向与逆向交织，有利于学生对几何对象与代数对象之间对应关系的理解，为后续要介绍怎样学习解析几何做好思想方法的铺垫。
教学片段2：
借助于对思考④的研究，揭示怎样学习解析几何。
思考：
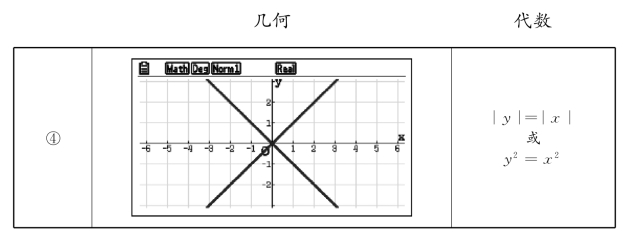
以具体研究思考④中的几何对象为例。先请学生观察这个几何对象，用数学语言表述出这个几何对象是满足怎样条件的一些点的集合（或轨迹）。
然后请学生写出这个几何对象在平面直角坐标系中所对应的代数对象——|y|＝|x|或y2＝x2。
接着研究这个代数对象所具有的性质。（x，y）是该方程的解，则（－x，y）、（x，－y）、（－x，－y）也是该方程的解。
于是，由代数对象即方程所具有的性质可以得到几何对象应该具有的几何性质，即关于x、y轴以及原点对称。
通过思考④的研究，揭示怎样学习解析几何，如下流程：对于一个几何对象，通过建立坐标系，得到相应的代数对象，研究这个代数对象所具有的代数性质，从而得到这个几何对象所具有的几何性质。
设计说明：
围绕方法论的角度展开教学。以思考④为例，引出在解析几何中研究几何问题与几何性质的一般方法——对于一个几何对象，通过建立坐标系，得到相应的代数对象，研究这个代数对象所具有的代数性质，从而得到这个几何对象所具有的几何性质。让学生了解该怎样学习解析几何，以及这是一门建立在方法论基础上的学科。
教学片段3：
反复环节：
此环节中，我们再次回到思考②、③，让学生通过反复再次体验如何通过对代数对象的研究得到其对应的几何对象所具有的几何性质，以巩固上述总结的“怎样学习解析几何”的一般流程。
设计说明：
这里通过反复，借助于对思考②、③的回顾，增进学生对解析几何本质的了解，增添了学生对“怎样学习解析几何”的体验与感受。
教学片段4：
递进环节：
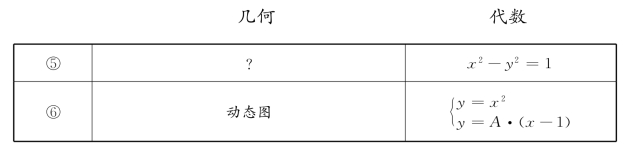
变式——思考④中的代数对象也可以表示成x2－y2＝0，把方程右端的0改为1，自然过渡到思考⑤中的代数对象x2－y2＝1。
对思考⑤，先给出代数对象x2－y2＝1，请学生研究其代数性质，从而得到其对应几何对象所应具有的几何性质。
这里可引导学生从以下三方面研究方程x2－y2＝1的代数性质：
1.研究x，y范围；
2.关于对称性的研究（按思考④的方式进行）；
3.既然有对称性，不妨尝试研究第一象限图像的特点，其余象限的几何性质可以通过对称性得到（此处可引而不发，适当留白）。
思考：
深化——研究思考⑥，引导学生思考如何研究方程组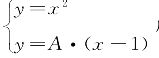
所具有的代数性质，从而得到平面直角坐标系中抛物线和直线之间具有的几何关系。
设计说明：
相对于思考②、③和④，思考⑤和⑥有难度上的提高，主要是涉及了还没有学习的双曲线和直线与抛物线的位置关系。思考⑤和⑥，通过变式和深化，让学生在更高层次的问题上再次经历研究方法上的思维体验之旅，类似于音乐旋律中的表现手法“模进”，以敲实“在解析几何中通过研究代数对象的代数性质来得到相应几何对象的几何性质”这种研究几何问题的方法。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
