线性方程组与矩阵

时间：2022-02-12 理论教育版权反馈

【摘要】：而上面这个与线性方程组相联的矩阵称为线性方程组的增广矩阵。所谓线性方程组的系数矩阵，就是去掉最后一列常数项得到的数表：。为了解线性方程组我们可以对这个矩阵的行进行运算，这些运算恰恰对应于消元过程中对方程进行的运算。世界上最早最完整的线性方程组解法记载在《九章算术》方程章中。

在初中我们学习了如何求解二元一次与三元一次线性方程组。我们先通过一个三元一次方程组为例说明一下当时的处理方法。

例：解方程组：

解：由（1）-（2）消去z，得到

x-y=5（4）

由（1）×3-（3），消去z，得到

8x+4y=91（5）

由（4）（5）联立，得到一个二元一次线性方程组

由（4）×4+（5），消去y，得到12x=111。

解这个一元一次方程，得到，把这一结果代回（4）式，得到。把x, y的值代回（3）式，可得。

容易看到，这种解线性方程组的思路是逐次消元。如果给出的是三元一次线性方程组，这种以前所使用的通常的消元法的思路是：取其中两组方程，从每组方程里把一个相同的未知数消去，各得到一个只剩两个未知数的方程，再从这两个方程中消去一个未知数。简言之，先将三元一次线性方程组转化为一个二元一次线性方程组，然后通过进一步消元得到一个一元一次线性方程。最后的方程可解，然后回代，整个线性方程组得解。

可以看到，这种消元过程很花时间。特别是，如果方程组含有的未知量比较多时，用这种思路会让计算变得非常复杂与烦琐。

仍以上面的题目为例，我们来看一种新的方法。

解：第一步，使方程第一个方程中x的系数为1。如果方程组的第一个方程本身满足条件，当然就不用做任何处理了。如果方程组的第一个方程不满足这一条件，那么我们可以看一下方程组中其他方程是否满足x的系数为1，如果有这样的方程，那么我们可以通过交换两个方程的位置来实现“使方程组第一个方程中x的系数为1”的要求。如果方程组中所有方程的x的系数都不为1呢？也很简单，只要取其中一个方程，设它里面x的系数为a，于是让此方程两边同乘以1/a即可。

对上面的线性方程组，可以看到（3）式中恰好x的系数为1，于是我们可以交换（1）式与（3）式的位置，得到：

第二步，把第一个方程后面的各个方程中的x消去。以上述方程组为例，我们只需（2）-2×（1），（3）-3×（1）即可。于是可以得到：

第三步，使第二个方程中y的系数为1。对本例，可让（2′）×（-1）即可。于是可以得到：

第四步，把第二个方程后的方程中的y消去。对本例，可让（5）×4+（6）即可。于是可得到：

第五步，使第三个方程中z的系数为1。

如果还有更多的方程，我们可以用同样的方式处理。这里没有第四个方程了，所以我们的步骤至此为止。

第六步，回代。把代入（2″）式，得到。再把y, z的值代入（1″）式，得到。

对我们得到的这个新的与原线性方程组同解的方程组，我们称为严格三角形的方程组。而为了得到这种形式的方程组，我们在上面的消元过程中用到了三种可以保持方程组同解的运算：交换两个方程的顺序；一个方程乘一个不为零的常数；把一个方程的常数倍加到另一个方程上去。如果一个n个方程n个未知量的线性方程组有唯一解，那么反复运用这三种运算，并通过上面非常有条理的操作方式，我们总可以把这一线性方程组化为与之同解的严格三角形方程组。一旦实现了这一步，剩下的工作变得非常简单，只需要依次回代即可。于是原来的线性方程组得解。

分析上面求解线性方程组的一般步骤，我们可以注意到，在求解过程中，重要的是变量所处的位置，而不是表示它们的符号。换言之，未知数用什么记号来代表是无关紧要的，起决定作用的是未知数的系数和方程的常数项。因此，如果我们在每一个方程中都保持各变量的固定顺序，那么一个给定方程组就完全由系数和常数项决定了。于是，我们可以把系数和常数项分离出来，并按原来的行列次序写出，而得到一张数表。如上面的线性方程组可以用下面的一个数表来表示：

这样的数表，在数学中就称为矩阵。而上面这个与线性方程组相联的矩阵称为线性方程组的增广矩阵。加上“增广”两字是为了与线性方程组的系数矩阵相区别。所谓线性方程组的系数矩阵，就是去掉最后一列常数项得到的数表：。

在增广矩阵中，每一行表示一个方程。为了解线性方程组我们可以对这个矩阵的行进行运算，这些运算恰恰对应于消元过程中对方程进行的运算。这样，对增广矩阵我们就有如下三种行运算：两行互换；任一行的每个元素乘一个不为零的常数；把一行的每一元素的常数倍加到另一行的相应元素上。这三种运算统称为行的初等运算。于是，用消元法解线性方程组的过程就可以通过对增广矩阵的行施行初等运算来实现。

下面我们就用这种方式求解一下上面的线性方程组。求解的各个步骤与上面的求解步骤是完全对应的。如第一步是交换第一行与第三行的顺序；第二步，第一行每一元素乘以（-2）加到第二行，第一行每一元素乘以（-3）加到第三行；第三步，第二行每一元素乘以（-1）；第四步，第二行每一元素乘以4加到第三行；第五步，第三行每个元素都乘以1/12。

由此系数矩阵化成了一个三角矩阵，它正好对应于我们上面得到的严格三角形方程组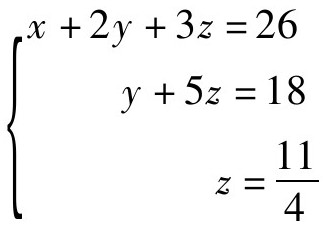：。使用回代法可以容易得到此方程组的解。

这种消元的方法在现代数学中被称为高斯消元法。高斯消元法是解线性方程组的最一般、最有效的方法。

在上述消元的基础上，我们还可以继续对增广矩阵施行行运算，使每一行的第一个“1”的上面诸项变为0。例如，在上面的例子中，我们可以在得到的结果后，继续把它转化：

由此得到的系数矩阵是一个单位矩阵（主对角线元素都是1，其余元素都是0），而此增广矩阵对应于方程组，显然这个矩阵已经把方程组的解直接表示出来了：x=9（1/4），y=4（1/4），z=2（3/4）。

这样的消元过程称为高斯—若当消元法。

高斯消元法在西方直到19世纪才由著名数学家高斯提出。中国早在1世纪下半叶就已经出现了与以上方法基本一致的完整的线性方程组解法，大大领先于西方。

世界上最早最完整的线性方程组解法记载在《九章算术》方程章中。中国古代的“方程”相当于现代的线性方程组，而“方程章”所探讨的就是线性方程组的求解问题。当时在解线性方程组时，要排列算筹，用算筹把方程各项的系数、常数依序排成一个方形的形状，然后通过移动算筹求解线性方程组，而其运算过程，与上面所提到的矩阵变换相当，因而可以说“方程章”中已经出现了世界上最古老的矩阵及矩阵初等运算。

下面，我们就以“方程章”的第1题为例，来看一下中国古代是如何求解线性方程组问题以及如何在这一过程中引入矩阵及矩阵变换的。

方程章第一题：“今有上禾三秉，中禾二秉，下禾一秉，实三十九斗；上禾二秉，中禾三秉，下禾一秉，实三十四斗；上禾一秉，中禾二秉，下禾三秉，实二十六斗。问上、中、下禾实一秉各几何”。

答曰：上禾一秉，九斗、四分斗之一，中禾一秉，四斗、四分斗之一，下禾一秉，二斗、四分斗之三。

方程术曰，置上禾三秉，中禾二秉，下禾一秉，实三十九斗，于右方。中、左禾列如右方。以右行上禾遍乘中行而以直除。又乘其次，亦以直除。然以中行中禾不尽者遍乘左行而以直除。左方下禾不尽者，上为法，下为实。实即下禾之实。求中禾，以法乘中行下实，而除下禾之实。余，如中禾秉数而一，即中禾之实。求上禾，亦以法乘右行下实，而除下禾、中禾之实。余，如上禾秉数而一，即上禾之实。实皆如法，各得一斗。

题目中“禾”指稻子一类的庄稼，“秉”指捆，“实”指打下来的如谷子一类的粮食。于是，这一题用现代语言表述即：现在有上等稻子三捆，中等稻子二捆，下等稻子一捆，合起来得谷子39斗；有上等稻子二捆，中等稻子三捆，下等稻子一捆，合起来得谷子34斗；有上等稻子一捆，中等稻子二捆，下等稻子三捆，合起来得谷子26斗。问，一捆上等稻子、中等稻子、下等稻子分别得谷子多少斗？

设上、中、下禾各一秉打下来的谷子数分别为x、y、z，则根据题目已知条件可列出如下的三元一次方程组：

现在我们依照“方程术”看看中国古代是如何解决这一问题的。“方程术”中首先提到的一段话——“置上禾三秉，中禾二秉，下禾一秉，实三十九斗，于右方。中、左禾列如右方”——讲的是通过摆放算筹建立方程组的方法。依照术文给出的算筹的摆放方法，可以得到如下摆放的一个筹式图。

可以看到，当时并没有引入表示未知数的符号，而是把我们所说的未知数的系数和常数排列成了一个筹式图。如果与上面列出的方程组对照，会注意到，这种排列是把第一个方程的各个系数及常数项3、2、1、39列在右方，同样将第二个方程，第三个方程的各个系数及常数项列在中行及左行。这种排列符合中国古代书写习惯：列自右而左，各元素从上而下采用竖排的方式记出。

而这种排成方形的筹算表达式正是中国传统数学中“方程”的本来意思。“方”指用算筹表示方程组各项未知量系数时的形状为方形；而“程”可理解为具有计量、考核性质的数值表达式。换而言之，对一个问题来说，如果含有若干个相关数据，将这些数据并肩排列成方形，则称之为“方程”。因此，中算中所谓的“方程”给出的实际上是一个线性方程组，而就其表现形式看，则相当于现代数学中线性方程组的增广矩阵。事实上，把上面筹式图中的算筹数字换作阿拉伯数字即，再把整个图转90°，就得到我们所熟悉的形式：这正是线性方程组系数的增广矩阵。

“方程术”后面部分是说明如何通过筹算解这一线性方程组。我们具体解释一下。

第一句“以右行上禾遍乘中行而以直除。”里面涉及两个名词。遍乘说的是，用方程某行某物（即未知数）的系数乘另一行的各项；而“直除”中的“除”如我们前面已经介绍过的，不是我们平常所理解的“做除法”，而是指“减”，“直除”即连续减去原行。减的次数没有限定，总之减到不能再减为止。合起来，遍乘直除是说：欲消去乙行某项系数，先用甲行该项系数乘乙行所有的项（称为遍乘），然后用得到的方程去减甲行，直到乙行该项系数化为0为止。实际上是减乙行该项系数那么多次。

我们举一个简单例子说明一下这种“遍乘直除法”。看如下简单的线性方程组。

为了消去这一方程组中第二个方程（2）中的x项，可以如此做：先第二行所有数字都乘以第一行中x的系数5（此即为“遍乘”），得到10x+25y=40；然后用这一式子连续减去第一行（此即为“直除”），事实上只需要减两次，即可消去x项，得到21y=20。

在理解了“方程术”中的这种关键算法后，我们再来看一下如何通过它求解最初给出的线性方程组。为了理解上的方便，我们先把筹算中的右、中、左三式改为横式的上、中、下三式，并以现代通用的阿拉伯数字代替算筹数字，则上述筹式相当于下列矩阵：

于是，用“遍乘直除法”解这一线性方程组的演算程序如下：

第一步，以上禾x的系数（即第一行首项系数）3乘第二行各项，得到：

连续两次与第一行相应项相减，变（消去）第二行首项系数为零，停止相减，得到如下所示结果：

这一步即方程术中“以右行上禾遍乘中行而以直除”的意思。

第二步，同样以上禾x的系数（即第一行首项系数）3乘第三行各项，然后减第一行相应各项，变（消去）第三行首项系数为零。得到如下所示结果：

此即为“方程术”中所说“又乘其次，亦以直除”的意思。

第三步，再以中禾y的系数（即第二行中间一项系数）5乘第三行各项，然后连续与第二行相应项相减（需要减四次），得：

此即为“方程术”中所说“然以中行中禾不尽者遍乘左行而以直除”的意思。

至此，对角线下面的几个数字已经全部都消为0。由此，系数矩阵变换为三角矩阵。而增广矩阵则等价于下述三角形方程组：

其后术文所述步骤，相当于在所得三角图示结果基础上进行代入法消元。用现代的方式表述为：由最后一行对应的方程36z=99中可解出z=2（3/4）。把z=2（3/4）代入中行“0、5、1、24”所对应的方程5y+z=24中，可得到y=4（1/4）。最后，把得到的y, z值代入上行“3、2、1、39”所对应的方程3x+2y+z=39中，可得到x=9（1/4）。

显然，整个求解过程与现代的线性方程组矩阵解法相当一致，而其消元方法则与高斯消元法基本一致。因此，方程术的提出表明中国古代数学家已经掌握了线性方程组的求解。但完善的线性方程组求解还有两方面问题需要解决。

一方面，可以看到在上面的例子中，方程组的每个方程都具有标准的形式，如三元一次方程组中的每个方程都是ax+by+cz=d。在这种情况下，即便没有表示未知量的符号，也没有把各项联结起来的加减号与等号，仍然可以用类似于矩阵的方式清楚地表示出方程组。具体而言就是如上面所做的，方程组中不同的未知量依靠该未知量系数的位置来表示，放在每一行的上面，常数项放在每一行的下面。然而，在由已知条件建立方程的过程中，一般来说，用方程术并不一定能直接得到上面的形式。在出现这种情况时应如何处理？

另一方面，如果细心，会注意到在这一个例子中，线性方程组中的各个方程系数都是正数，而且在消元过程中也没有出现负数。此时，运用“方程术”可以列出并解出线性方程组。但如果出现负数项或者方程的系数虽为正但在消元过程中出现负数时，该如何处理？

对此，中国古代数学家分别引入损益术与正负术有效地解决了这两方面的问题。

为了解损益术，我们举方程章第2题为例：今有上禾七秉，损实一斗，益之下禾二秉，而实一十斗。下禾八秉，益实一斗与上禾二秉，而实一十斗。问上、下禾实一秉各几何？

用我们现在的思路，设x为上禾一秉之实，y为下禾一秉之实。于是依题意可列出方程组：

如果直接把方程中的各系数排放在一起，显然会造成混乱。这种情况下，为了得到标准形式的方程组，中国古代数学家引入了损益术。所谓损益术，用现在的术语来说可以理解为一种通过移项建立方程的方法，《九章算术》方程章说：“损之曰益，益之曰损。”即是说，在等式一端损，相当于在另一端益；在等式一端益，相当于在另一端损。这相当于现在方程理论中的移项变号法则，即移负为正，移正得负。

于是对上面的例子，经过损益可得到变形后的方程组为：

于是通过损益常数项，得到了一个标准形式的二元一次方程组。然后就可以按前面的方法进一步求解这一方程组了。鉴于建立标准形式方程组的需要，在《九章算术》方程章的其他例子中除损益常数项外，还损益未知数，甚至也包括现在所谓的合并同类项。由此可见，《九章算术》在对方程“复原”和“对消”的理解方面，不逊于后来阿拉伯有关论著，而在时间上则比后者要早得多。然而，非常可惜与遗憾的是，损益术在中国古代只被看做建立方程组要用到的一种必不可少的辅助方法，在处理一次方程时却始终未能变换为这种方式，使经常能轻而易举可解的问题要用其他方法（经率术）解。

更值得一提的是，为了解决第二方面的问题，在对“方程”的研究中，中国古代数学家提出了中国古代数学最杰出的创造之一：负数概念与正负数的运算法则。

在应用方程术时，有两种情况下会涉及负数。一是在列方程组时方程的各项系数或常数项可能会出现负数。比如，在某些实际问题中，既涉及卖出又涉及买入。如果考虑卖出可收钱，因此把卖出的数目看做为正，那么买入的数目就应看做为负。类似的，在出现余钱与不足钱或“益实”（加入谷子）与“损实”（减去谷子）时，前者若视为正，则后者应视为负。只有规定了这种正负，我们才可以根据实际问题列出相应的方程组。在上面所举的方程章第2个问题中，我们已经看到了因为这种原因所导致的负数的引入。二是在用遍乘直除法消元时，很可能会有小数减大数的情形。比如方程章第3个问题，根据题意可列出方程组。按照以上所介绍的解方程组的办法，第一步可以消去（3）式中的x，为此可以（3）×2-（1），但在此过程中y的系数会出现0-1。在此情形中，不引入负数方程的两行相消便不能畅通无阻，也就不能保障“直除”消元的顺利进行。

为了保证遍乘直除算法能畅行无阻，也为了扩大“方程”解决应用问题的范围，中国古代数学家比较自然地引入了负数。这是世界数学史上第一次突破正数的范围！后来，魏晋时期的著名数学家刘徽在对《九章算术》作注时对正、负数给出比较科学的定义：“两算得失相反，要令‘正’、‘负’以名之”。“算”指算筹，刘徽的意思是说：如果计算时用算筹代表“得”，“失”两种量，那就要用正负数来定义。同时，刘徽指出在算筹中区别正负数的方法：“正算赤，负算黑，否则以斜正为异”。意思是说，正数用红色算筹，负数用黑色算筹。如果只有同色算筹的话，则遇到正数将筹正放，负数斜放。

对中国古代数学家首先引入正负数概念的伟大意义，前苏联著名数学史家尤什凯维奇普高度赞扬说：“在《九章算术》第八章中，破天荒第一次在科学史上看到了正量与负量的区分……”与中国人很早使用负数相比，国外对负数概念的引入则都晚得多。在古印度，7世纪数学家婆罗摩笈多晚于中国早于世界其他各国提出了负数概念，并用小点记在数字上面表示负数。12世纪的数学家婆什迦罗，则把负数理解为“负债”或“损失”。欧洲第一个给出负数解释的是斐波那契，他解决一个关于某人的赢利的问题时说：我将证明这问题不可能有解，除非承认这个人可以负债。

在负数引入后，一个紧联的问题是正负数的运算。为此，《方程》章中引入了“正负术”，即正、负数的加减运算法则：“同名相除，异名相益，正无入负之，负无入正之。其异名相除，同名相益，正无入正之，负无入负之。”

“同名”、“异名”即同号、异号；“相益”、“相除”指两数（绝对值）相加、相减。“无入”是指由零减去或加上。用现代语言解释前半段即是说：同符号两数相减，等于其绝对值相减；异符号两数相减，等于其绝对值相加；零减正数得负数，零减负数得正数。这半段给出的是正负数的减法法则。相应地，后半段给出的是正负数的加法法则，用现代语言解释即是说：异符号两数相加，等于其绝对值相减；同符号两数相加，等于其绝对值相加；零加正得正，零加负得负。显然，“方程章”给出的正负数加减法法则都是正确的。

有了正负术，线性方程组加减运算就圆满解决了。与正负数概念的引入一样，《九章算术》中的正负术也是世界数学史上第一次引入正负数的加减法则。而就时间上看，中国负数概念和正负数加减法则的提出超前其他民族几个世纪，甚至上千年。可以说，中国古代数学所取得的这一伟大成就是遥遥领先的。

然而中国古代在对负数的认识与运用方面也有令人感到遗憾之处。一方面，根据现在资料，直到北宋刘益引入负系数开方之前，在中国古代数学著作中，负数概念仅用于方程术即线性方程组解法。另一方面，中国古代关于正负术乘除运算的引入也大大推迟了。在《九章算术》中没有涉及正负术的乘除运算，而在此后极长的时间内，包括刘徽在内的数学家都小心谨慎，把用到正负数乘除运算之处化为累加或累减进行，尽量避免出现负数乘除。于是，直到元代朱世杰《算学启蒙》（1299），中国才出现了关于正负数乘除运算的明确记载：“同名相乘为正，异名相乘为负”，“同名相除所得为正，异名相除所得为负”。至此，中国才对有理数的四则运算法则做出了全面总结，而这已经晚于古印度几个世纪了。

如上所提到的，中国古代解线性方程组的方法最早记载在我国古代数学经典著作《九章算术》方程章中。这里，我们有必要对这本被称为“算经之首”的中国古典数学名著作一下简单介绍。

《九章算术》是我国古代最主要的一部传于后世的数学著作。最晚成书于1世纪下半叶，作者不详。很可能在成书前经多人之手，并经多次整理、修改、补充而成，是多位汉代学者集体创作的结晶。作为一部承前启后的著作，一方面它总结了西汉及西汉以前的数学成果，集当时数学之大成。另一方面，它对后来中国数学的发展产生了极其深远的影响。由于内容深刻、广博，它一问世就占据了中国数学舞台的中心位置。它的出现，标志着中国古代数学体系的形成。

《九章算术》共收有246个数学问题，包括方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章。其体例统一为：“今有……问……几何。答曰：……术曰：……”全书以计算为中心，任何问题都要计算出具体的数字作为答案，而其术文，全部是公式和计算程序，即现在经常所说的算法。它集中体现了中国古代数学体系的特征：以筹算为基础，以算法为主，寓理于算，广泛应用。

反过来，《九章算术》的问世进一步塑造了中国古代传统数学，它的框架、形式、风格和特点深刻影响了中国古代数学的发展。在它之后，中国的数学著述基本上采取两种方式：一是为《九章算术》作注，其中以魏晋时期杰出数学家刘徽的《九章算术注》（263）最知名最重要，其中包含了刘徽本人丰富多彩的创见和发现。二是以《九章算术》为楷模编纂新的著作。其“术文挈领应用问题形式”成为后世数学著作的标准微观结构形式。而数学理论密切联系实际的风格和以计算为中心的特点，在中国也由此被牢固确立下来。

作为中国古代最重要的数学典籍，《九章算术》从成书直到明末西方数学传入之前，一直是学习数学者的首选教材，历史上多次作为朝廷颁定的首选数学教科书行用，对中国古代数学的发展起了巨大的作用。而且书中的许多理论，直接为中国数学的发展奠定了基础.如现代著名数学家吴文俊（1919～）所说，《九章算术》“直到明代以前，向为中国数学上各种重大发现的源泉”。

恰当地说，这本被誉为中国古算经之首的中国数学经典，于中国和东方数学，大体相当于《几何原本》之于希腊和欧洲数学。在世界古代数学史上，两者像两颗璀璨的明珠，东西辉映，前者所代表的算法体系，与后者代表的公理化体系旨趣既异，途径亦殊，成为现代数学思想方法的两大源泉。

作为一部世界科学名著，《九章算术》在隋唐时期即已传入朝鲜、日本。现在，它又被译成俄、德、法等多种文字。

《九章算术》的内容十分丰富，在算术、代数、几何等学科的许多领域都取得了十分重要的，在当时可以说是领先于世的数学成就。在所介绍的开方术以及这里所介绍的方程术都是典型的例证。特别是，可代表《九章算术》最高数学成就的方程章，更是以其精彩纷呈的内容抒写了中国古代数学最灿烂的一页。

《九章算术》方程章中共计18题，其中二元的8题，三元的6题，四元、五元的各2题。在第1题后提出了“方程术”，作为全章的纲。其中所使用的消元法相当于现在严谨的矩阵初等变换法。其基本思想是顺序消元，对增广矩阵反复使用初等变换，最终使系数矩阵成为三角形矩阵，从而得解。这种方法正是现在的高斯消去法。

之后在第2题后提出“损益术”；在第3题后提出“正负术”，作为列、解方程组的主要方法，成为方程术的必要补充。“损益术”体现了中国古代对方程“复原”和“对消”的深刻理解；“正负术”中则引入负数概念与正负数的加减运算。这都是中国古代数学杰出的发现，也是数学史上破天荒的大事。

在有了“方程术”又佐以“损益术”、“正负术”后，已经足以列出任何一个方程组，并足以对任何一个线性方程组消元了。正如书中在其他问题后的“术”中写道：“如方程，损益之”，或者“如方程，以正负术入之”，或者是这三者的结合。在《九章算术》成书的时代，就如此圆满地解决了线性方程组布列与求解，真可谓是世界数学史上的一个奇迹。正因此，后来清代数学家梅文鼎高度推崇中国古代的方程术，认为它是传统代数学中“最精之事”。日本数学史家三上义夫称方程术出类拔萃，是世界首创。前苏联数学史家别列兹金娜对方程术亦评论说：“19世纪高斯的研究成果：乘、减图式与中国‘方程’术一致。在这电子计算机时代，不论方程个数是多少，用这种图式终能得解。不料中国人在古老的年代里能在筹算板上获得这种解法。”她赞扬方程术内容是统一的，结构是严谨的，叙述是简洁的。

确实，以现在的观点看，方程章所提出的线性方程组解法是《九章算术》最值得称道的成就。它不但是中国古代数学中的伟大成就，在世界数学史上，亦可谓一颗璀璨明珠。

《九章算术》方程章给出世界上最早最完整的线性方程组解法，开创了此后中国数学在这一领域中辉煌成就的先河。后来数学家刘徽在其《九章算术注》中又对这一解法的正确性作了理论说明，建立了直除消元法的理论基础。此外，刘徽还对线性方程组有确定解的条件做了说明。他指出，为了让“方程”有确切解，要“皆如物数程之”和“行之左右无所同存”。即线性方程组的方程个数必须与“未知数”即物数的个数相同，而且在同一方程组中，不能出现两行数字相同或有相同的比率（用现在的话说就是不能有相依方程）。至于线性方程组解的存在性，刘徽指出，要“有所据而言耳”，即每行必须合于实际而有所依据，也即不得有矛盾方程。可见，刘徽已经了解到线性方程组有确切解的条件：方程组的个数须与未知量个数相同；方程组中不允许存在同解的方程（左右无所同存）；每个方程不能是虚构的无解方程，而是来自实际的有解方程（有所据）。可以看到，刘徽的这一认识是深刻而全面的。

除了在“方程”理论方面的建树外，刘徽还改进了“方程”的消元方法。

我们看到“方程术”中的关键算法是“遍乘直除”。这种消元的方法和现在代数学中通用的方法在实质上是一致的。但是在具体操作中，由于直除法消元要反复相减，显然比较烦琐。

对此，刘徽创造了更简便的互乘相消法。我们以方程章第7题“牛羊直（同值）金”为例说明一下。这一题目是说：“今有牛五，羊二，直金十两；牛二、羊五，直金八两。问牛、羊各值金几何？”

用现代表示法，设x, y分别表示牛、羊值的金数，于是依题意可列出方程组：。刘徽用2乘第一行，用5乘第二行，得，两行相减，一次即可消去x项，得出21y=20，y=20/21。

这种互乘相消法正是我们现在所熟悉的“加减消元法”。刘徽说，以小推大，此种方法“虽四、五行不异也”。他已经完全清楚，这种方法是一种普遍的方法，可以应用于四元、五元等更多元方程组的情形。

显然，互乘相消法比直除相消法简便得多。但遗憾的是，刘徽的这种先进思想，后世近千年未引起重视，人们更多时候仍然采用直除法。直到南宋秦九韶才完全废止直除法，全部使用互乘相消法。

中国古代关于线性方程组的求解在南宋著名数学家秦九韶手中被进一步完善。在《九章算术》及刘徽的工作基础上，他对线性方程组解法又做了一些改进，创立了更为规范的矩阵解法。最能体现其这方面工作的是其《数书九章》中的“均货摊本”一题。

秦九韶提出的问题大都比较复杂。我们这里只介绍“均货摊本”问题的一部分。

这一部分是说：有甲乙丙丁四人出海经商。出海前四人入股资本计：甲黄金200两，盐40袋；乙白银800两，盐264袋；丙度牒15张，白银1670两；丁度牒52张，黄金58（1/3）两。恰好，四人入股资本各值钱10600贯文。问：黄金（两）、白银（两）、度牒（张）、盐（袋）各值多少？

如设黄金每两值x贯文，盐每袋值y贯文，白银每两值z贯文，度牒每张值w贯文，按题意可列出方程组：

在列出这一四元一次线性方程组后，秦九韶完满地求解了它。而且特别值得注意的是，《九章算术》中对“方程”的求解只有“术”无“草”，而《数书九章》中则既有“术”又有“草”，其草完整地保留了消元法的步骤。就本题而言，秦九韶认真写出运算细节的草文达1500字，更重要的是本题“草”中有一系列筹算图，计15幅，且各有名称，如第一图为“首图”。用现在的观点看，这个首图相当于一个增广矩阵。以下依次为“次图”、“定率图”……“终图”。整个演算过程井然有序，非常整齐、漂亮。把这些图稍微变一下形式即可成为一系列增广矩阵，而其演算过程则相当于现代矩阵变换的过程。在具体演算中，秦九韶还改进了线性方程组解法，普遍用互乘相消法代替《九章算术》中的“直除法”。而在使用互乘相消法消元前，如果方程系数有公因数，秦九韶就先各项约去公因数，以简化运算。事实上，秦九韶在这一方程组的求解过程中，反复地采用这种“化约—互乘—相消—化约”的步骤。就计算量上来说，这种算法不一定是最合理的。然而，这种相当于增广矩阵初等变换的算法却极具规范性。此外，在矩阵变换过程中多处出现负数，从这些算式可见秦九韶对“方程”法则和正负法则掌握非常熟练。

最后，秦九韶得到如下所示的终图（其中算筹数字已改为阿拉伯数字）：

显然，秦九韶所得到的终图中，系数矩阵已化成了单位矩阵。因此，秦九韶的整个演算实质上是由增广矩阵转化为单位矩阵的详细过程。这改变了此前将系数方阵只化到三角方阵为止的做法，相当于高斯—若当消元法。

我国自秦汉以来结合正负术，用《九章算术》方程术解多元线性方程组，至此达到非常完善的程度。而秦九韶用中国数码字记录的自己解题的筹算整个过程，更是提供了我国线性方程组消元法的重要的实物证据，通过这一详细演算实录所提供的真凭实据，后人得以真正看到当时的具体演算，这使它具有极高的史料价值，弥足珍贵。

在国外，多元一次方程组的解法最早出现在古印度数学家婆罗摩笈多的著作中（约628年）。欧洲关于线性方程组的研究更晚得多。

欧洲最早提出三元一次方程组解法的是16世纪法国数学家比特奥（约1492～1564）。1559年，在《算术》中他开始用不同的字母表示不同的未知数，并用不甚完整的（因为那时欧洲尚未接受负数）加减消元法解一次联立线性方程组。到17世纪，莱布尼兹等人开辟了用行列式解线性方程组的道路。18世纪，法国数学家贝祖在《数学教程》（1764～1769）一书中提出用联立方程组的系数构成行列式，以此求解方程组或判断该方程组是否有解。

直到19世纪，德国数学家高斯提出了与《九章算术》中方法实质相同的方法，并用它解决了天体计算和后来的地球表面测量（这种涉及测量、求取地球形状或当地精确位置的应用数学分支称为测地学）计算中的最小二乘法问题。所以这一消元方法在西方被称为高斯消去法。后来，W·若当在一本测地学手册中提出现在所称的高斯—若当消元法。

从时间上来说，《九章算术》的解法实在是世界数学史上一大光辉的成就，高斯远远晚于中国。因此，近年来也有西方人开始对这一方法改变称谓，如法国科学院院士、原苏黎世大学数学系主任P.Gabriel教授在他撰写的教科书中就称解线性方程组的消元法为“张苍法”，张苍相传是《九章算术》的作者之一。

上面我们介绍了用高斯消元法求解一类行与列相同的线性方程组，最终我们通过对增广矩阵的行施行初等运算，把系数矩阵化成了一个三角矩阵，从而得解。

在更一般的情况下，我们仍然可以借助高斯消元法对增广矩阵的行施行初等运算，只不过最终得到的系数矩阵不一定是三角矩阵了。下面我们举几个例子。

例：解方程组