稀疏矩阵的运算

5.3　稀疏矩阵的运算

由于采用压缩存储的方法,稀疏矩阵运算的实现变得复杂起来。本节中将讨论稀疏矩阵的几种基本运算,并讨论相关运算在某一种存储结构下的实现方法。

1.初始化稀疏矩阵

创建一个三元组顺序表,主要是对三元组顺序结构进行初始化。具体算法实现如下。

该算法的时间复杂度为O（1）。

2.销毁稀疏矩阵

销毁一个稀疏矩阵的前提是必须有一个稀疏矩阵存在。采用三元组顺序表存储矩阵M时,销毁矩阵的具体算法实现如下。

该算法的时间复杂度为O（1）。

3.稀疏矩阵输出

稀疏矩阵在输出时,主要是根据所给出的三元组顺序表来输出该稀疏矩阵。由于稀疏矩阵采用压缩存储方式,所以其输出方式有输出三元组信息和输出完整的稀疏矩阵两种。

（1）输出稀疏矩阵三元组信息的具体算法实现如下。

算法时间复杂度为O（M.t）。

（2）输出完整的稀疏矩阵的具体算法实现如下。

该算法中每个矩阵元素都要输出,输出语句的执行次数等于矩阵中元素的个数。因此,该算法的时间复杂度为O（m×n）。

4.稀疏矩阵复制

将稀疏矩阵的复制,即由矩阵M通过复制得到一个完全一样的稀疏矩阵T。采用三元组顺序表存储矩阵M和T时,具体算法实现过程如下。

该算法时间复杂度为O（M.t）。

5.稀疏矩阵转置

转置是一种最简单的矩阵运算,对于一个m×n的矩阵M,其转置矩阵T是一个n×m的矩阵,并且T_ji＝Mij（i＝0,1,…,m－1,j＝0,1,…,n－1）。矩阵M和其转置矩阵T如图5－13所示。

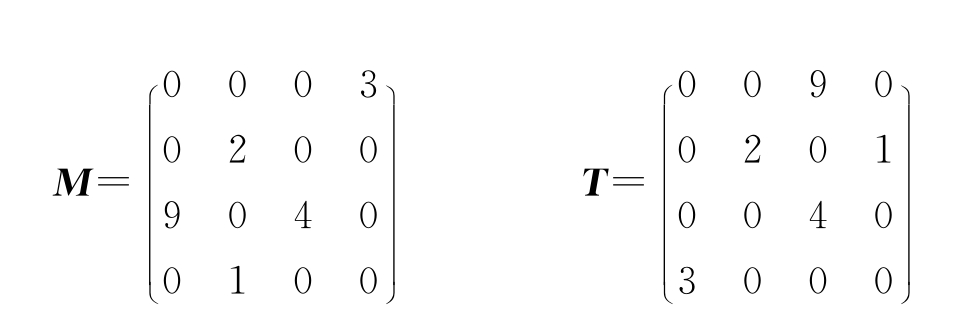
图5－13　矩阵M及其转置矩阵T

矩阵的转置本质上就是交换矩阵每一个元素的行值和列值,因此稀疏矩阵中非零元素的个数不会减少。当用三元组顺序表表示稀疏矩阵时,求转置矩阵的元素就变为由M的三元组表求得T的三元组表的问题。要实现转置必须处理以下两个问题。

（1）将稀疏矩阵M中非零元素的行、列值相互交换,即将M.data[]中每个元素的i,j值相互交换。

（2）因为三元组顺序表中元素以行优先顺序排列,T.data[]中元素顺序和M.data[]中元素顺序不同,所以需要重排三元组顺序表中的元素次序。

为了解决上述问题,可采用以下算法实现矩阵的转置。

（1）按照T.data[]中三元组的次序依次在M.data[]中找到相应的三元组进行转置,即按照矩阵M的列序进行转置。其具体算法如下。

该算法主要工作在col和p的双重循环中完成,因此算法时间复杂度为O（M.n×M.t）。当非零元素个数与M.m×M.n同数量级时,时间复杂度会增加到O（M.m×M.n²）,效率将会大大降低。算法效率低的原因是每转置一个元素,都必须对M.data[]从头到尾扫描一遍。

（2）按照M.data[]三元组顺序进行转置。转置后的元素不连续存放,而直接存放到T.data[]中对应的位置上。

为此,设置两个辅助数组num[M.n＋1]和cpot[M.n＋1]分别存放矩阵M中每一列非零元素的个数和每一列第一个非零元素在T.data[]中的位置。其具体算法如下。

从空间上看,算法（2）中多使用了两个辅助数组,因此其空间复杂度为O（n）；从时间上来看,算法使用了4个并列的循环,分别执行了M.n次、M.t次、M.n－1次、M.t次,因此算法的时间复杂度为O（M.n＋M.t）。

6.稀疏矩阵相乘

两个矩阵相乘,即

Q＝M×N

其中,M是m₁×n₁矩阵,N是m₂×n₂的矩阵,并且n₁＝m₂。矩阵M和N相乘的经典算法如下。

该算法时间复杂度为O（M.m₁×M.n₁×N.n₂）。

当M、N是稀疏矩阵并用三元组压缩存储时,乘积矩阵Q中元素为

其中,1≤i≤m1,1≤j≤n₂。

为求得Q的值,只需要在M.data和N.data中找到相应的各对元素（即M.data中的j值和N.data中的i值相等的各对元素）相乘即可。即为了得到非零的乘积,只要将M.data中的每个元素（i,k,M（i,k））找到N.data中所有相应的元素（k,j,N（k,j））相乘,为此需要在N.data中寻找矩阵N中第k行的所有非零元素。行逻辑链接的顺序表结构中提供了非零元素的位置表,采用此结构来计算稀疏矩阵相乘则较为方便。

采用行逻辑链接顺序表实现矩阵相乘运算必须处理以下两个问题。

（1）求累计和值。矩阵相乘,对于M.data[p]（p＝1,2,…,t）来说,需要找到N中所有满足条件M.data[p].j＝N.data[q].i的元素N.data[q],再求M.data[p].e和N.data[q].e的乘积。由于矩阵Q中每个元素值是个累计和,为便于计算,应对每个元素设一个累积和的变量,设其初值为零,然后扫描数组M,求得相应元素的乘积,累加到适当的求累计和的变量上。

（2）乘积结果压缩存储到Q.data[]中。两个稀疏矩阵相乘不一定是稀疏矩阵,由于乘积Q的每一个分量都是一个累加值,即使M（i,k）×N（k,j）不为零,其累加值Q[i][j]也可能为零。因此乘积Q中的元素是否为非零元素,只有累加之后才能得知。由于Q的行号和M的行号一致,而M是按行存储的,因此可对Q逐行处理,并将累计求和的结果压缩存储到Q.data中去。

因此,两个稀疏矩阵相乘的算法可描述如下。

上述算法中,累加器ctemp初始化时间复杂度为O（M.m×N.n）,求得Q的所有非零元的时间复杂度为O（M.t×N.t/N.m）,进行压缩存储的时间复杂度为O（M.m×N.n）。因此,该算法的总的时间复杂度为O（M.m×N.n＋M.t×N.t/N.m）。

7.稀疏矩阵相加

矩阵相加操作,即Q＝M＋N,要求执行相加运算的两个矩阵M和N有相同的行数和列数。执行相加操作时,M和N对应位置上（M_ij、N_ij）的元素相加并存放到Q的相应位置Q_ij。对于稀疏矩阵,假设Q、M和N均采用三元组顺序表存储,当扫描三元组顺序表M和N的行号时,会出现以下几种情况。

（1）如果M当前项的行号与列号等于N当前项的行号和列号,则将对应元素值相加。如果结果不为0,则存储到Q的三元组顺序表。如果M当前项的行号等于N当前项的行号,M当前项的列号小于N当前项的列号,则将M当前项存储到Q的三元组顺序表,否则将N当前项存储到Q的三元组顺序表。

（2）如果M当前项的行号大于N当前项的行号,则将N当前项存储到Q的三元组顺序表。

（3）如果M当前项的行号小于N当前项的行号,则将M当前项存储到Q的三元组顺序表。

（4）如果M中还有未扫描项,则将M的剩余项依次存储到Q的三元组顺序表。

（5）如果N中还有未扫描项,则将N的剩余项依次存储到Q的三元组顺序表。

稀疏矩阵相加的具体算法描述如下。

该算法通过三个while循环将M、N中所有的非零元素都扫描一遍,因此总的执行次数为M.t＋N.t,该算法的时间复杂度为O（M.t＋N.t）。

算法采用三元组顺序表存储矩阵,比较适合非零元素的位置和个数发生变化不大的矩阵相加运算。当两矩阵相加,非零元个数和位置发生较大变化时,宜采用十字链表的存储结构。