矩阵的相似

1.6.5　矩阵的相似

本段假定A是n阶方阵.

1.特征值与特征向量

给定一个n阶方阵A，如果数λ与非零列向量x满足

Ax=λx或(A－λE)x=0，

那么称数λ为A的特征值，称非零向量x为A的对应特征值λ的特征向量.

记f(λ)=|A－λE|，这是一个关于λ的n次多项式，称f(λ)为矩阵A的特征多项式，称一元n次方程f(λ)=0为特征方程.特征方程的根就是方阵A的特征值.n阶方阵A有n个特征值，其中包括实数特征值与虚数特征值，且重根按其重数计算个数.

设λ₀是A的一个特征值，即|A－λ₀E|=0.这时，齐次线性方程组(A－λ₀E)x=0必定有非零解，全体非零解向量都是A的对应于特征值λ₀的特征向量.

2.特征值的性质

设λ₁，λ₂，…，λ_n是n阶方阵A的特征值，A=(a_ij)_n×n.

①λ₁+λ₂+…+λ_n=a₁₁+a₂₂+…+a_nn，

λ₁λ₂…λ_n=|A|.

②A^T的特征值也是λ₁，λ₂，…，λ_n.

③A为奇异阵的充分必要条件是λ₁，λ₂，…，λ_n中至少有1个是0.

④当A为可逆阵时，A－1的特征值是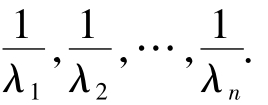

⑤φ(λ_i)是φ(A)的特征值，i=1，…，n，其中多项式φ(λ)=a₀+a₁λ+…+a_mλ^m，矩阵多项式

φ(A)=a₀E+a₁A+…+a_mA^m.

⑥当A是n阶实对称阵时，特征值λ₁，λ₂，…，λ_n全是实数.

3.特征向量的性质

给定n阶方阵A，则:

①相应特征值λ₀的特征向量必定有无限多个;

②每个特征向量只能相应一个特征值;

③相应不同特征值的特征向量必定线性无关;

④当A是n阶实对称时，相应于不同特征值的特征向量必定正交，且有n个两两正交的特征向量.

4.矩阵的相似

给定两个n阶方阵A、B.如果可逆阵P满足

P^－1AP=B，

那么称矩阵A与B相似，称B是A的相似矩阵.可逆阵P称为相似变换矩阵.

①当A与B相似，B与C相似时，A与C相似.

②当A与B相似时，A与B的秩相等，且A与B等价.

③当A与B相似时，A与B的特征多项式相同，从而A与B的特征相同，且|A|=|B|.

5.矩阵的相似对角化

当n阶方阵A与对角阵Λ相似时，即可逆阵P满足

P^－1AP=Λ

其中

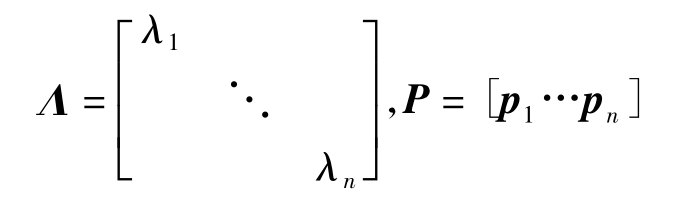
那么λ₁，…，λ_n恰是A的特征值，且p_i恰是A的对应特征值λ_i的特征向量，i=1，…，n.

定理13n阶方阵A能与对角阵相似的充分必要条件是:A有n个线性无关的特征向量.

判断n阶方阵A能否与对角阵相似常用以下两种充分条件.

①当A有n个不同特征值时，A能与对角阵相似.

②当A有n阶实对称阵时，A能与对角阵相似.

n阶方阵A与对角阵Λ相似的定义给出了求Λ与变换矩阵P的方法.但要注意有相等特征值的情况.例如，某个特征值重复出现3次(即特征方程有3重根)，则相应要找出3个线性无关的特征向量.如果不存在3个线性无关的特征向量，那么A不能与对角阵相似.

【例1.6-35】已知方阵A满足|A+2E|=0，则A必定有特征值(　).

(A)1　(B)2　(C)－1　(D)－2

解:特征多项式f(λ)=|A－λE|在λ=－2处的值恰是f(－2)=|A+2E|=0.这表明λ=－2是特征方程f(λ)=0的根，－2是A的特征值.故选(D).

一般地，如果已知|aA－bE|=0，a≠0，那么，由

推得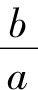是A的特征值.

【例1.6-36】设3是方阵A的特征值，则A²+A－2E必有特征值(　).

(A)3　(B)10　(C)4　(D)不能确定

解:由于多项式φ(λ)=λ²+λ－2，A²+A－2E=φ(A)，因此，φ(A)必有特征值

φ(3)=3²+3－2=10.

故选(B).

【例1.6-37】已知3阶方阵

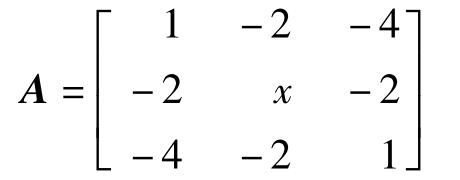
的特征值为－4，5，y，则x，y分别等于(　).

(A)－1，0　(B)2，3　(C)4，5　(D)1，1

解:由－4是A的特征值推得|A+4E|=0，即

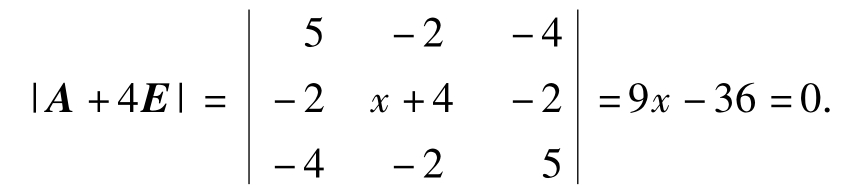
因此解得x=4.故选(C).

本题没有求出y的值不能令人放心.由特征值的性质①，从x=4及

－4+5+y=1+x+1

解得y=5.

【例1.6-38】设3阶方阵

试求A的特征值与3个线性无关特征向量，并判断这些特征向量是否正交?

解:首先求特征值.特征多项式

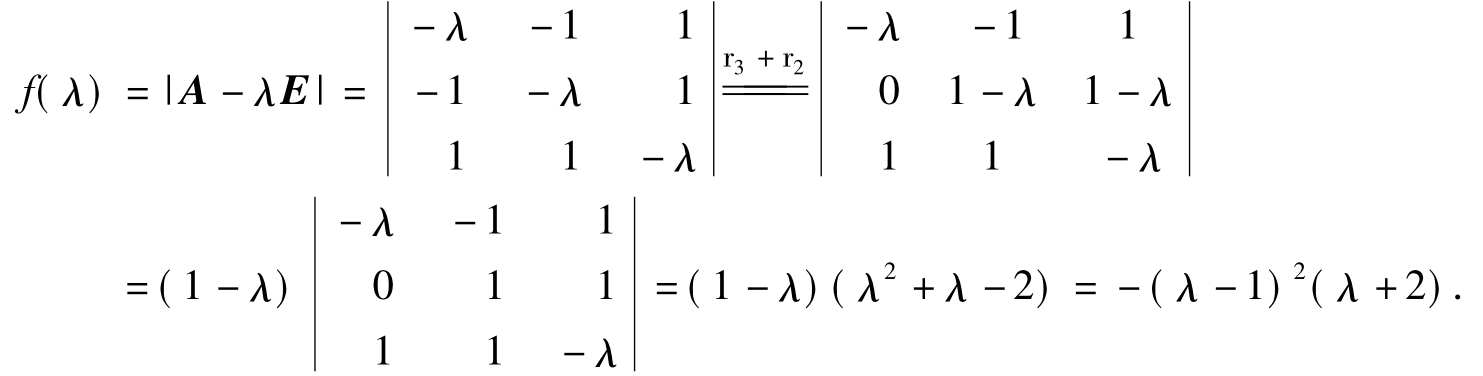
于是A的特征值是－2，1，1.

当λ=－2时，求特征向量相当于解齐次线性方程组(A+2E)x=0.由系数矩阵

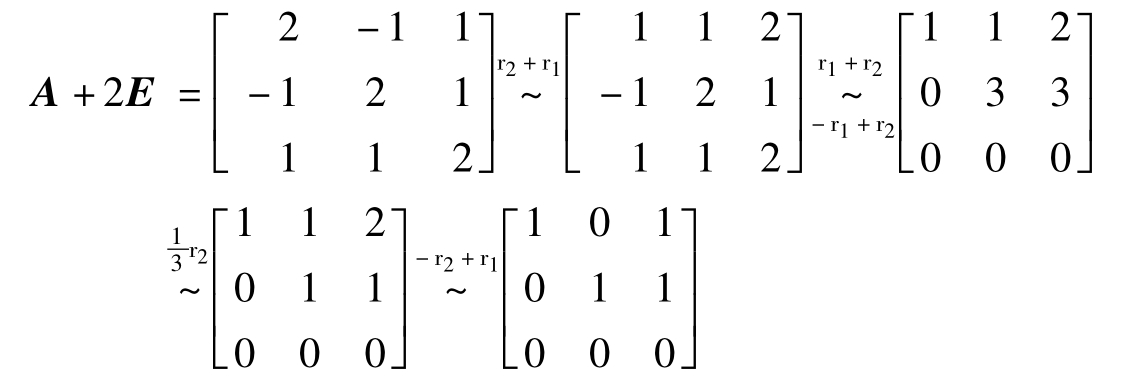
得到一个特征向量p₁=［－1，－1，1］^T.

当λ=1时，求特征向量相当于解齐次线性方程组(A－E)x=0.由系数矩阵

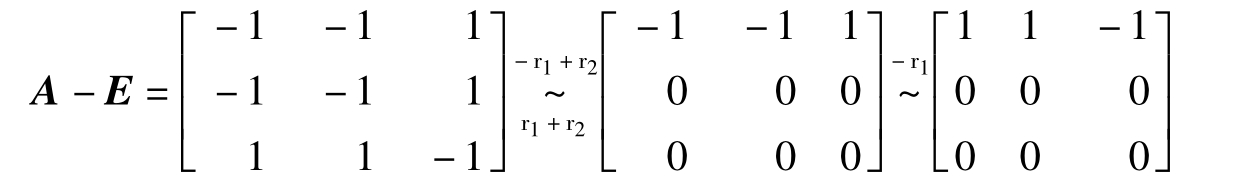
得到两个特征向量p₂=［1，0，1］^T，p₃=［－1，1，0］^T.

由于P=［p₁p₂p₃］的行列式不等于0，因此p₁，p₂，p₃是A的3个线性无关的特征向量.

p₁与p₂正交，因为［p₁，p₂］=(－1)×1+(－1)×0+1×1=0.由于A是实对称阵，p₁，p₂分别是不同特征值下的特征向量，因此它们必定正交.按特征向量的性质④，A有3个两两正交的特征向量.尽管p₃与p₁正交，但p₃与p₂不正交.这表明，即使A是实对称阵，相应同一特征值下的特征向量未必一定正交.但是，如果在特征值λ=1下取特征向量p₄=［－1，2，1］^T，可以验证p₁，p₂，p₄是两两正交的特征向量组.

由于A是实对称阵，A必定能与对角阵相似.由矩阵的相似对角化方法得知，对角阵Λ与相似变换阵P分别为

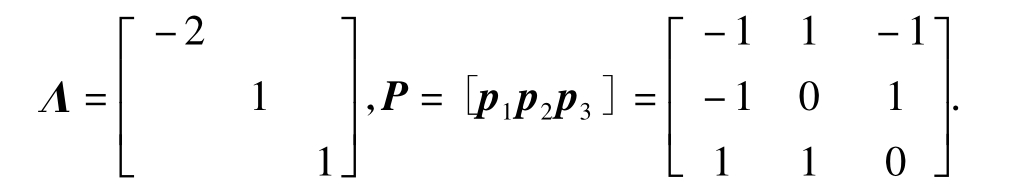
它们满足P^－1AP=Λ.相似变换矩阵不唯一.如果取变换矩阵Q=［p₁p₂p₄］，可以验证Q－1AQ=Λ.

【例1.6-39】下列方阵中，不能与对角阵相似的是(　).

解:(A)与(C)都是对称阵，它们必定能与对角阵相似.(B)中矩阵有3个不同特征值，它必定能与对角阵相似.故选(D).

记(D)中矩阵为A，它的特征值λ=λ₀、λ₀.求特征向量相当于解齐次线性方程组(A－λ₀ E)x=0.由于R(A－λ₀E)=1，因此基础解系由1个解向量组成.这表明2阶方阵A仅含1个线性无关的特征向量，A不能与对角阵相似.

说明A不能与对角阵相似也可以用反证法来处理.由于A的特征值λ=λ₀、λ₀，因此，如果A能与对角阵相似，那么必定存在可逆阵P，使得P^－1AP=Λ，其中Λ=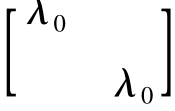=λ₀E.于是，A=PΛP^－1=P(λ₀E)P^－1=λ₀E.这与已知A≠λ₀E相矛盾.