河谷文明与多项式方程

历史学家往往把兴起于古埃及、美索不达米亚、古中国和古印度等地域的古代文明称为“河谷文明”，而早期数学就是在尼罗河、底格里斯河与幼发拉底河、黄河与长江、印度河与恒河等河谷地带首先发展起来的。从可考证的史料看，古埃及与美索不达米亚的数学在年代上更为久远，只是在公元前均告衰微，崛起稍晚的古中国与古印度数学则延续到公元之后并在中世纪臻于高潮。

在这一节中我们将简单介绍古埃及与美索不达米亚这两个河谷文明在求解多项式方程方面取得的成就，对古中国和古印度这方面的贡献将放在第二节中做介绍。

人们对古埃及数学知识水平的了解主要来自幸存至今的两部纸草书。一部叫莱茵德纸草书。这一纸草书因1858年为苏格兰收藏家莱茵德收藏而得名。它是由公元前1650年左右一位名叫阿姆士（A′hmose）的人抄录的。书的开头写道：“准确的计算。阐明一切黑暗的、秘密的存在事物的指南”。后世就以此作为书名。根据书的前言还知道，阿姆士并非书的原著者，其实他抄录的是一部已经流传了两个多世纪的更古老的著作。但为纪念抄录者，这一纸草书也称阿姆士纸草书。

另一部称为莫斯科纸草书，1893年它为俄罗斯收藏者获得，1912年转为莫斯科博物馆所有，并因之得名。据研究，它出自约公元前1890年一位佚名作者之手。

这两部纸草书是古埃及最重要的传世数学文献。它们都是各种类型的数学问题集。莱茵德纸草书主体部分由84个问题组成，莫斯科纸草书则包括了25个问题。在这些问题中，有些可以归之为今天所说的代数方程的范畴。我们剖析其中一个简单例子来看一下。

上图是莱茵德纸草书第24题的僧侣文原文，第一个字如下图所示

读音类似“阿哈”（aha）或“呵”（hau），意思是“一堆”，相当于方程中的未知数。整个题目可意译为：已知“堆”与七分之一“堆”相加为19，求“堆”的值。

古埃及人对此问题的解法比较有趣。他们先把7作为未知数的实验值，代入得数8，但应得结果是19，这两个结果之比是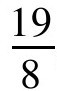。于是将7乘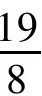即得出正确的答案。

莱茵德纸草书第26个问题也使用了这种技巧。这个问题可意译为：求一未知数，它与自身相加结果为15。纸草书中的解法如下：假设答数为4，那么4加4的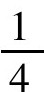为5……找一个乘5能得到15的数，答案是3。用4乘3，答案是12。

这种解法被称为“假位法”，实质上它是一种算术方法：先假设一个特殊的数作为“堆”值，将其代入等号左边去运算，然后比较得数与应得结果，再通过比例方法确定未知数的真值。

对此，著名数学史家史密斯曾评述说：“世界竟曾经为形如ax+b=0的方程所困惑过，这似乎是不可思议的，但是古代数学家为解这种方程，却确实曾求助于一种比较烦琐的方法，这种方法后来在欧洲称为‘假位法’”。这种假位法是莱茵德纸草书中普遍使用的方法。因其过程采用了一次假设，故也叫“单假设法”。

不过，有时埃及纸草书中也使用我们现代的方法来求解一次方程。例如，莫斯科纸草书中有一个例子是：求一个数，它的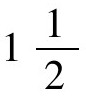倍加上4等于10。用现代的记号表示，即，其解法是：首先由10减去4得6，然后将6乘以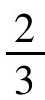，得解为4。

在纸草书中，古埃及人还求解了相当于形如x+ax=b或x+ax+bx=c的一次方程。除了含有一个未知数的一次方程问题外，古埃及人还研究并处理了简单的二次方程。如在一部柏林纸草书中有一个问题：把一个面积为100的正方形分为两个小正方形，使其中一个的边长是另一个的3/4。用现在的形式表示为：

容易看到，从这一问题可引出一个二次方程。有意思的是，古埃及人对此的处理也是使用的假位法。其解题思路是：先假设x=1，则，右端是边长为5/4的正方形面积，而题目中大正方形边长是10，两者的比是10:5/4=8，因此将原假设的边长扩大8倍，得x=8，而y=8×3/4=6，此即为原问题的正确答案。

可以看到，他们解决了相当于ax2=b类型的最简单的二次方程。

美索不达米亚文明（习惯上又称为巴比伦文明）大约在公元前3500年出现于底格里斯和幼发拉底的两河流域。人们对其的了解来自保存至今的约50万块泥板。

古巴比伦人曾用尖芦管在湿泥板上刻写楔形文字，然后将泥板晒干或烘干。后来，人们挖掘出大量这种不易毁的泥板。这些被保存下来的泥板中大约有300多块属于数学文献。它们主要分属两个相隔遥远的时期。一大批是公元前2000年头几个世纪的遗物，还有许多则来自公元前一千年的后半期。通过研究这些泥板文书，人们发现古巴比伦人在多项式方程求解方面表现出高度的技巧，取得了十分可观的成就，达到了相当的高度。

对一次方程，或许是觉得简单，古巴比伦人没有过多探讨。在留下的资料中很少有单个的这类方程，并且没有提供求解的算法。如一块泥板上有这样的问题：一块石头，加上它的1/7，得到一个重量，在这个重之上再加它的1/11，得到1马那（mana，重量单位），问这块石头有多重？这问题相当于方程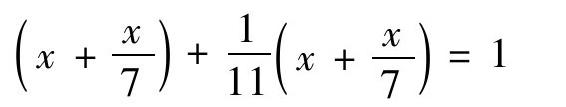，可解得x=77/96马那。原答案是正确的，但没有解题的过程。

我们已看到古埃及人主要讨论的是一次方程，对于二次方程则仅涉及最简单的情形ax2=b。与之不同，古巴比伦人的突出成就恰恰表现在求解二次方程方面，这也是他们的一个主要研究领域。事实上，许多古巴比伦泥板上列有大量的二次方程。例如，有一块泥板文书中有这样的问题：已知依几布姆（igibum）比依古姆（igum）大7。问依几布姆和依古姆各为多少？

这里igibum和igum是古巴比伦数学文献中表示互为倒数（即乘积为1）的两个数的专有术语。值得注意的是，古巴比伦人在这里相当于用记号表示了未知量。另外需要说明的是，古巴比伦人使用60进制，igibum与igum乘积为1，1指一个大单位，相当于60个小单位，而问题中的7则是小单位。于是若以x表示igibum, y表示igum，则上述问题相当于求解方程组：

如我们所熟知的，这可转化为求解一个二次方程x2-7x-60=0，古巴比伦人给出算法：。这相当于对二次方程x2-px-q=0使用了求根公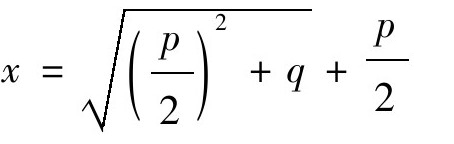，这与我们更熟悉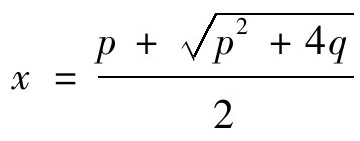显然是等价的。

古巴比伦人也给出了另一类似问题——求一个数，使它和它的倒数之和等于一个给定的数——的正确解法。

进而，古巴比伦人还研究并解决了更具一般性的一种标准形式：已知两数的和与积求此两数。对要求的两未知量，他们使用的单词是长（us）、宽（sag），对两者的积使用的单词是面积（asa）。所要解决的问题与问题的陈述都使人想到，古巴比伦人想处理的是矩形的面积、周长与边长之间的关系，事实上他们研究的这种标准形式相当于：已知矩形的周长与面积，确定矩形的长与宽。这一问题的求解在古代既重要又迫切，因为当时人们普遍有一种错误认识：矩形的面积完全取决于它的周长。许多懂得更多的人就利用这一点欺骗他人，在占便宜的同时还赢得了慷慨的名声，其办法是自己要周长较小面积较大的土地，而给别人周长较大却面积较小的土地。

不过，随着时间的推移，这一问题的几何意义逐渐失去，“长”“宽”这些几何术语也慢慢地成为表示未知量的标准做法，并演变成抽象的代数符号，相当于我们熟悉的x、y。因此，古巴比伦人研究的这种标准形式用现代的代数语言来叙述就是：已知x+y=p, x·y=q，求x, y。

古巴比伦人用下述5个步骤求这两数：取p的一半；将此数平方；从中再减去q；对所得结果开平方；再加p的一半得出所求两数中的一数，从p中减去这个数得出另一个数。

容易明白，他们所解的方程组可转化为二次方程：x2-px+q=0。而他们的五步解法，用现代代数语言来写就是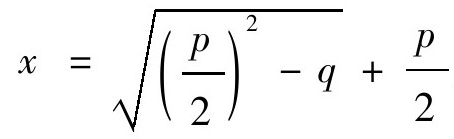：，y=p-x。这与我们更熟悉的形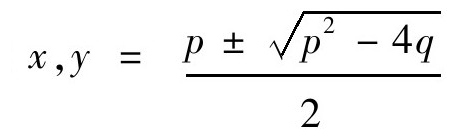自然是等价的。

除求解由方程组获得的二次方程外，古巴比伦人也求解单个的二次方程。如有这样一个问题：一正方形的面积与它的一条边的4/3之和为11/12，求其边长。

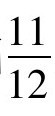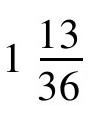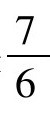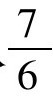用现代的术语来说，就是要解方程。古巴比伦人求解的步骤与方法是：取的一半，得，取的平方，得，然后将这个结果加到上去，得，这个值是的平方。从中减去，这就是所需要的边长。这一算法可以容易地翻译成现代求解方程x2+bx=c的公式，即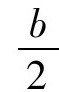。可以看得出来这是二次方程求根公式的一种形式。

还有一个问题如下：如果某正方形的面积减去其边长得870，问边长是多少？用现代的代数语言即解方程x2-x=870，泥板给出的解法是：取1的一半，得1/2；以1/2乘以1/2，得1/4；把1/4加在870上，得3481/4，它是59/2的平方，59/2再加上1/2，结果是30。这一算法可以容易地翻译成现代求解方程x2=bx+c的公式，即。可以看得出来这也是二次方程求根公式的一种形式。

此外，古巴比伦人还研究并给出了x2+c=bx形式方程的正确解法。

可以看到，古巴比伦人把不缺项二次方程分成了不同的形式并分别求解，现代读者可能会对此深感困惑。古巴比伦人为什么不像我们现在所做的那样把二次方程统一处理而非要自找麻烦呢？道理在于，古代没有负数概念。因此，方程的系数、常数及方程的解都必须是正数。这样，要研究的不缺项二次方程就被分成三种基本类型：x2+bx=c、x2=bx+c、x2+c=bx（其中b、c均为正数），而且要对不同的类型分别求解。通过后面的介绍，我们会明白这种分类处理方程的方式在数学上延续了相当长的时期。

所有这三类方程在古巴比伦泥板文书中都可以找到，并都给出了正确的解算程序。而古巴比伦人也清楚如何把给定的二次方程转化成上面三类方程之一。因而，可以说古巴比伦人已经圆满地解决了二次方程的求解问题，这在古代特别是几千年以前是相当非凡的成就。不过，需要指明的是，古巴比伦人并没有真正地使用与我们今天相同的多项式方程概念，其解法也都是通过文字叙述指出求解的步骤。事实上，其所谓的算法是由一个接一个简练的短语或句子组成，没有“等号”或其他简洁符号。自然，因为没有符号表示法，所以他们也不可能给出我们现在所使用的一般二次方程的求根公式，他们所能做的只能是给出具体例题，并通过这些具体例子的求解来说明一般解法。也正是由于没有符号表示法，他们在解题时才会遇到那么多困难。这样的困难是代数语言系统发展起来以前人们不得不面对的。

此外，古巴比伦人虽给出了求解的正确步骤，但却没有说明每一步做法的理由。后人对此做出一些推测，比如“已知x+y=p, x·y=q，求x, y”，古巴比伦人的思路可能如下：若取x=p/2和y=p/2，则满足x+y=p，但不一定满足x·y=q。因此，这解应有误差，假设误差是z，则可设真正的解x=p/2+z和y=p/2-z。于是。由此可以得。进而，可得出x, y。

除有效地解决了一般的不缺项二次方程外，古巴比伦人还处理了古埃及人未曾探讨过的三次方程。像最简单的x3=a，主要通过查立方表或立方根表来求解。事实上，为了使计算简捷，古巴比伦人曾编制了大量的数学用表。在现有的300多块数学泥板文书中，就有200多块是数学用表，包括乘法表、倒数表、平方表、立方表、平方根表、立方根表，甚至还有指数表、对数表。对形如x3+x2=a的混合三次方程，他们也是借助现成的表来求解，因为古巴比伦人编有专门的n3+n2的数值表（其中n为整数）。

对一个特殊三次方程144x3+12x2=21的解决显示了他们在解方程方面的高超水平。古巴比伦人先运用了代换的方法：用12乘方程两端，并设y=12x，从而把方程转化为y3+y2=252，查表得y=6，因此x=1/2。在没有现代符号的情况下，能够认识到方程（ax）3+（ax）2=b与y3+y2=b本质上属于同一类型，这种初等的代数变换思想，在当时是了不起的成就。

古巴比伦人在研究中还涉及并解决了简单的四次方程。比如泥板中有这样一个问题：“我把长乘宽得面积10。我把长大于宽的量自乘，再把这个结果乘以9。这个面积等于我把长自乘所得的面积。问长和宽是多少？”

如我们上面已经介绍到的，这里的文字长、宽，只不过是两个未知量的方便说法，相当于我们的x、y。于是这个问题用现代的符号可表示为：

在解这一方程组时，会得出x的一个四次方程。但其中缺少x和x3项，因而可作为x2的二次方程来解。古巴比伦人给出了这一问题的正确答案。

通过上述的介绍，我们看到古巴比伦人可以圆满解决一次、二次方程，可以求解部分特殊的三次、四次方程，其在多项式方程研究方面取得的可观成就在古代数学中确实是非常突出的。