一、资金时间价值
(一)资金时间价值的概念
在工程经济计算中,无论是工程完成后所发挥的经济效益还是工程建造中所消耗的人力、物力和资源,最后都是以价值形态,即资金的形式表现出来。资金是劳动资料、劳动对象和劳动报酬的货币表现。资金运动反映的是物化劳动和活劳动的运动过程。在这个运动过程中,劳动者在生产劳动过程中新创造的价值形成资金增值。这个增值采取了随时间推移而增值的外在形式,故称之为资金的时间价值。
由于资金存在时间价值,致使不同时点发生的资金流量不能直接进行比较。资金必须与时间结合,才能表现出其真正的价值。
资金时间价值的表现形式是利息和利润。对于储蓄投资来说,表现形式为利息,即放弃使用资金所获的报酬。因为对于投资者由于出借资金,因而它就不能用于消费或其他投资,因此它的福利损失或其他投资损失就要用利息来补偿;对项目投资来说,表现形式为利润。由于项目投资存在着风险和机会成本,因此只有当未来项目的收益能显著超过目前的投资时,人们才会赞成这笔用于增加资金的支出,即投资该项目,而这种由于时间所产生的价值就是投资的利润。
利息和利润是衡量资金时间价值的绝对尺度,其多少和投资额有关,所以在项目技术经济分析中往往用利率作为衡量资金时间价值的相对尺度。在实践中,社会平均的资金收益率通常用作资金时间价值的衡量尺度,用R表示。R=R 1+R 2+R 3。R1是考虑时间因素补偿的收益率;R2是考虑通货膨胀因素补偿的收益率;R3是考虑风险因素补偿的收益率。
(二)利息和利率
1.利息
利息是占用资金所付代价或放弃使用资金所获报酬,它是资金时间价值的一种体现,它是资金在某一固定时间间隔后(一般为1年)所得到的增值。在借贷过程中,债务人支付给债权人超过本金的部分就是利息。
I=F-P (3-22)
式中:I——一定时期内所得的利息额;
P——本金;
F——本金与利息之和(简称本利和)。
2.利率
利率是指在一定时期内所得利息额与借贷本金的比率。利率期间通常以1年为期,也有小于1年的(如半年、季、月或天)。用以表示利率的时间单位称为计息周期(计息期)。
i=I/P×100% (3-23)
式中,i为利率。
3.利息的计算
当一项经济活动的计息周期在一个以上时,利息的计算方式有两种,单利和复利。
(1)单利的计息方式。单利是指在计算利息时,仅对投入的本金计算利息,上一个计息周期产生的利息在下一个计息周期不再计息,即不考虑利息的时间价值。其利息的计算公式如下:
I=P×i (3-24)
而n期末单利计息方式的本利和F等于本金加上利息,即
F=P(1+i·n) (3-25)
式中,n为计息次数。
在利用上述公式计算本利和F时,要注意式中i的计息周期和n的时间单位要一致。此外单利法的隐含假设是每年的盈利不再投入到社会再生产中,这不符合资金运动的实际情况。故在工程经济分析中要采用复利的方法计算利息。
(2)复利的计息方式。为了使借款及投资活动中所有的货币都按同样标准产生时间价值,那么对尚未支付的利息也应当以同样的利率计算利息,即“利生利”、“利滚利”,这种计算方法就是复利。计算公式为
I t=I×F t-1 (3-26)
式中:It——第t个计息周期的利息;
Ft-1——第t-1期期末的本利和。
而n期末复利计息方式的本利和F等于
F=P(1+i)n (3-27)
4.名义利率和实际利率
利率的一定时期通常以年为单位,它可以与计息周期相同也可以不同。在工程经济中由于采用复利的计息方式,当利率的时间单位和计息周期不一致时,就出现了名义利率和实际利率。
(1)名义利率。名义利率是指计息周期利率i与利率的时间单位内计息周期数m的乘积。名义利率为年利率,用r表示。
r=i×m (3-28)
若月利率为1%,则年名义利率为12%。很显然,计算名义利率时忽略了前面各期利息再生利息的因素,这与单利的计算相同。
(2)实际利率。实际利率是将利率时间单位内的利息再生因素考虑在内计算出的利率,即用利率时间单位内产生的总体利息与本金之比,也称为有效利率,用R表示。根据利率的概念,即可推导出名义利率和实际利率的关系。
若利率的时间单位为年,在1年内计息rn次,则年名义利率为r,计息周其利率为i=r/m。设年初有本金P,根据复利的计算公式,一年后的本利和为

根据利息的定义,1年内的利息(利率时间单位内产生的总体利息)I为
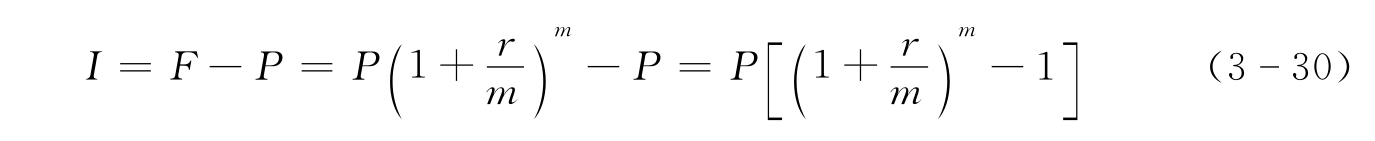
再根据实际利率的定义可得年实际利率R为
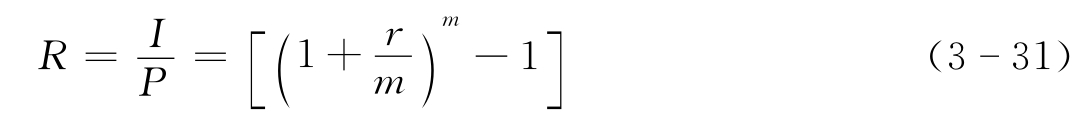
例如,若年名义利率为6%,按月计息,则年实际利率为
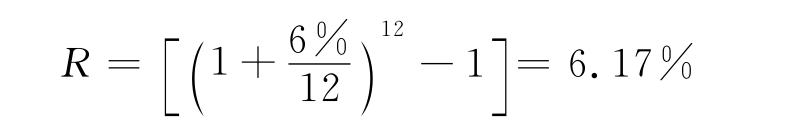
可见,名义利率与实际利率在数值上是不相等的。除年计息一次时名义利率等于实际利率之外,实际利率一般大于名义利率。
(三)现金流量及现金流量图
1.现金流量
设备投资的目的是为了将来获得更大回报,因此投资的定义可以是:为期望取得利润而支付出去的资金。所以在设备建造过程中存在着复杂的资金运动,这种不断运动的资金流就成为现金流量。流入这个过程的资金称为现金流入,流出这个过程的资金称为现金流出,现金流入用CI表示,现金流出用CO表示,同一时点现金流入与现金流出的差额叫净现金流量,用NCF表示。
NCFt=(CI-CO)t (3-32)
2.现金流量图
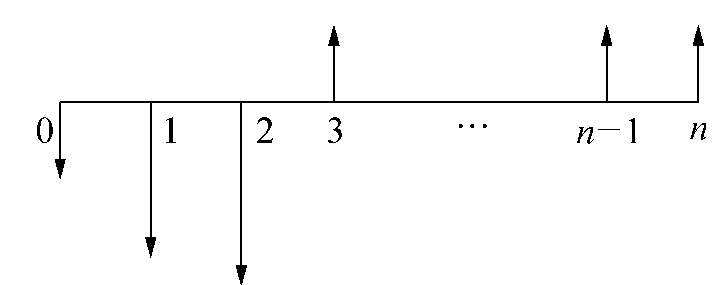
图3-1 现金流量图
把现金流量作为时间的函数,用一个二维的图形表示,叫现金流量图,见图3-1。运用现金流量图,就可以全面、形象、直观地表达出设备工程形成过程中经济系统的资金运动状态。现金流量图的画法如下:
(1)横轴表示时间轴,将横轴分为n等份,注意第n-1期终点和第n期的始点是重合的。每一等份代表一个时间单位,可以是年、半年、季、月或天。
(2)与横轴垂直向下的箭头代表现金流出,与横轴垂直向上的箭头代表现金流入,箭头的长短与金额的大小成比例;
(3)代表现金流量的箭头与时间轴的焦点即表示该现金流量发生的时间。
由此可知,要正确绘制现金流量图,必须把握好现金流量的三要素,即现流量的大小、方向、时间点。
现金流量图与出发点有关,从借款人角度出发和从贷款人角度出发所绘现金流量图不同。
例3-1 某人向银行借款5万元,年利率4%,5年后一次归还本利和为5(1+4%)5=6.0833万元,从借款人角度和从贷款人角度所绘现金流量图见图3-2和图3-3。项目经济评价是从贷款人角度对项目进行分析,即先有支出,后有收入。
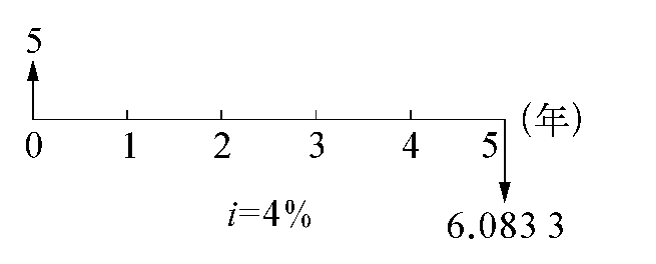
图3-2 借款人角度
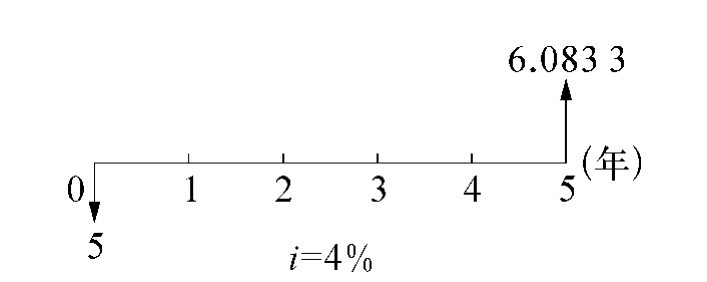
图3-3 贷款人角度
(四)资金等值变换公式
1.资金等值
由于资金具有时间价值,使得在不同时点上绝对数值不等的资金具有相等的价值,称为资金等值。也就是说,可以把任一时点上的资金变换为另一特定时点上的值,这两个时点上的两笔不同数额的资金量在经济上的作用是相等的。
把特定利率下不同时点上绝对数额不等而经济价值相等的若干资金称为等值资金。影响资金等值的因素有三个,即资金额的大小、计息期数、利率的大小。
2.等值变换公式
资金等值在工程经济中是很重要的一个概念,在分析一项投资活动是否值得进行的时候,就是要看该活动流入的价值是否大于流出的价值,而由于通常的经济活动投资在先,收益在后,所以就要想办法找出它们的资金等值,所利用的公式就称为资金等值变换公式。
设i为利率(折现率);n为计息期数;P为现在值,简称现值;F为将来值,简称终值;A为年度等值(或称等额年金),简称年值或年金。
(1)一次支付复利公式。
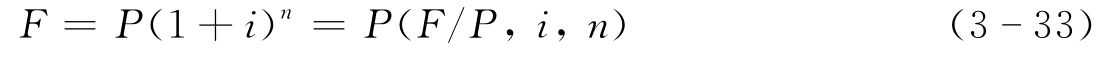
(F/P,i,n)称为一次支付复利系数或简称为终值系数。如(F/P,5,6)表示已知现值求终值,利率为5%,计息6期。
(2)一次支付现值公式。

(P/F,i,n)称为现值系数。如(P/F,5,5)表示已知终值求现值,利率为5%,计息5期。
(3)等额支付系列年金终值公式。
每期末金额相等的资金称为年金(如图3-4所示)。如果换算利率为i,则n期末的终值F与年金A之间的变换关系为
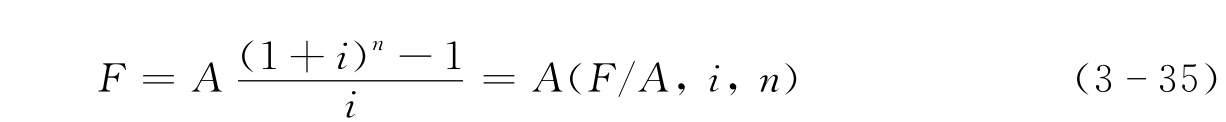
其中(F/A,i,n)称为年金终值系数,公式推导如下:
F=A(1+i)n-1+A(1+i)n-2+…+A(1+i)+A
两边同乘(1+i)得
F(1+i)=A(1+i)n+A(1+i)n-1+…+A(1+i)2+A(1+i)
以上两式相减得
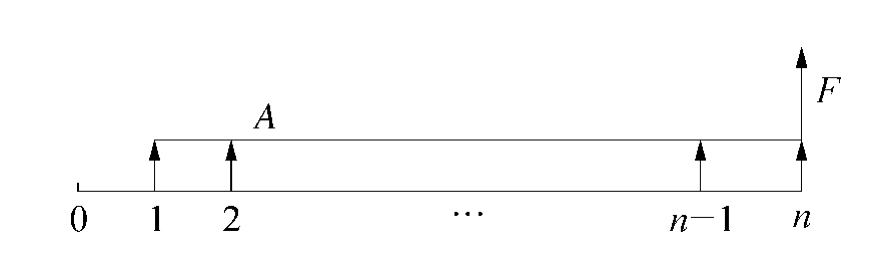
图3-4 现金流量图
(4)等额支付系列偿债基金公式。将终值F变换为n期内年金A的公式为
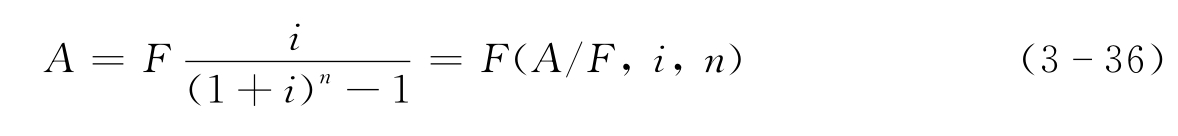
(A/F,i,n)称为偿债基金系数。
(5)等额支付系列年金现值公式。
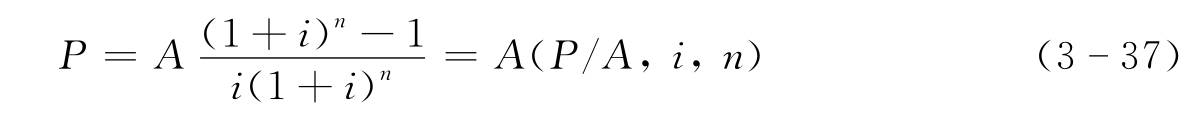
(P/A,i,n)称为年金现值系数。当n→∞时,此时的A称为永续年金,而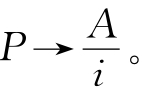
(6)等额支付系列资金回收公式。

式中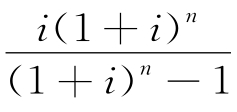 称为资金回收系数,记为(A/P,i,n)。当n足够大时,资金回收系数等于i。
称为资金回收系数,记为(A/P,i,n)。当n足够大时,资金回收系数等于i。
例3-2 某设备准备在5年后大修,需大修费用50万元,i=7%,问从现在起每年应存入多少钱以备将来大修所需?
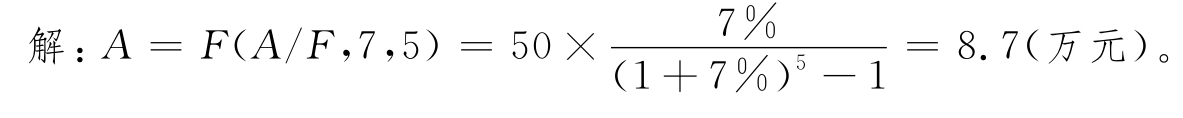
例3-3 某企业从银行贷款100万元,用于购买某设备,若偿还期为8年,每年末偿还相等的金额,贷款利率为7.2%,每年末应偿还多少?
解:这是一个已知现值,求年值的问题,所以有
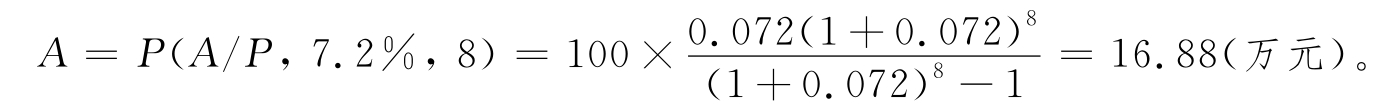
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















