土中附加应力

一、任务介绍

土中附加应力是因建筑物的荷载作用在地基中引起的，它是附加于原有自重应力之上的那部分应力。对一般天然土层来说，自重应力作用下的变形已稳定，而附加应力则是使地基发生变形、引起建筑物沉降的根本原因。因此要计算地基的变形，必须首先计算地基的附加应力。在均质地基中，通常采用弹性半空间模型，以弹性理论为基础求解地基附加应力。本任务主要介绍了地基中各种情况下附加应力的计算方法。

二、理论知识

计算地基附加应力时假定：①基础刚度为零，即基底作用的是柔性荷载；②地基是连续、均匀、各向同性的线性变形半无限体。下面介绍工程中常遇到的一些荷载情况和应力计算方法。

1．竖向集中力作用

集中荷载作用下地基中应力的计算是求解其他形式荷载作用下地基小应力分布的基础。在均匀的、各向同性的半无限弹性体表面作用一竖向集中力F时，半无限弹性体内任意点M的全部应力可利用布辛尼斯克解来计算，如图2－19所示。

图2－19 弹性半无限体在竖向集中力作用下的附加应力

在各个应力分量中，对建筑工程地基沉降计算直接有关的应力为竖向正应力σz。地基中任意点M的竖向应力的表达式为

式中：R——M点与集中力F作用点O的距离，

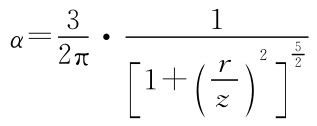竖向集中力作用下地基竖向附加应力系数，为r／z的函数，其值可查表2－2。

表2－2 竖向集中力作用下地基附加应力系数α

地基中附加应力的分布可由式（2－14）计算得出。由于竖向集中力作用下地基中的应力状态是轴对称空间问题，因此，地基中附加应力的分布规律可通过F作用线切出的任意竖直面来表示，如图2－20所示。

图2－20 在荷载轴线及不同深度上σz的分布

图2－21 σz等值线图

其分布规律可归纳如下。

（1）在地面下任意深度的水平面上，各点的附加应力非等值，在集中力作用线上的附加应力最大，向两侧逐渐减小。

（2）在集中力F的作用线上（r＝0），附加应力的分布随着深度的增加而递减。

（3）在r＞0的竖直线上．随着深度的增加，附加应力从小逐渐增大，至一定深度后又随深度的增加而逐渐变小。

（4）距离地面越远，附加应力分布的范围越广，如图2－21所示。

2．矩形基底受铅直均布荷载作用

实际工程中，土工结构物是通过—定尺寸的基础把荷载传给地基的。尽管基础的形状和基础底面上的压力始终各不相同，但都可以利用集中荷载下附加应力的计算方法和弹性体中的应力叠加原理，通过对面积分布荷载的积分，计要地基内任意点的附加应力。

设地基表面有一矩形面积，宽度为b，长度为l，其上作用着竖直均布荷载，荷载强度为P（实际计算时，采用基底附加压力，下同），确定地基内各点的附加应力时，先求出矩形面积角下的应力，再按叠加法原理进行计算，即可求得任意点下的附加应力。

1）角点下的附加应力

角点下的附加应力是指图2－22中所示的O、A、C、D四个角点下，任意深度处的附加应力，只要深度z相同，则四个角点下的附加应力值相同。将坐标原点取在角点O上，在荷载面积内任取微分面积d A＝dx·dy，并将其上作用的荷载以dp代替，则dp＝p·d A＝p·dxdy。求出该集中力在角点O以下深度z处M点所引起的竖直向附加应力dσz。

图2－22 矩形基底铅直均布荷载作用下角点下的附加应力

用式（2－16）沿整个矩形面积OACD积分，即可得矩形基础底面上均布荷载p在M点引起的附加应力。

式中：m＝l／b；n＝z／b。其中，l为矩形的长边，b为矩形的短边。

为计算的方便，可将式（2－17）简写成：

σz＝αcp 　（2－18）

其中，αc＝

式中：αc——矩形基础底面受竖直均布荷载作用角点下竖向附加应力系数，其值可从表2－3中查得。

表2－3 矩形基底受铅直均布荷载作用下的竖向附加应力系数

续表

2）任意点的附加应力

在实际工作中，常需计算地基中任意点的附加应力。如图2－23所示的荷载平面，求O点下的附加应力时，先通过O点做平行于矩形两边的辅助线，使O点成为几个小矩形的公共角点，分别求各矩形角点O下同一深度的附加应为，再利用应力叠加原理，求得O点的附加应力，此方法称为角点法。

图2－23 应用角点法计算O点下地基的附加应力

（1）矩形受荷面边缘任意点O以下的附加应力，如图2－23（a）所示。

σz＝（αc1＋αc2）p 　（2－19）

（2）矩形受荷面内，任意点O以下的附加应力，如图2－23（b）所示。

σz＝（αc1＋αc2＋αc3＋αc4）p 　（2－20）

（3）矩形受荷面边缘外侧，任意点O以下的附加应力，如图2－23（c）所示。

σz＝（αc1＋αc2－αc3－αc4）p 　（2－21）

（4）矩形受荷面角点外侧，任意点O以下的附加应力，如图2－23（d）所示。

σz＝（αc1－αc2－αc3＋αc4）p 　（2－22）

以上各式中αc1、αc2、αc3、αc4分别为矩形Ohbe、Ofce、Ohag、Ofdg的角点应力系数；p为作用在矩形面积上的均布荷载。

应用角点法时应注意以下问题：①画出的每一个矩形，都有一个角点O点；②所有画出的各矩形面积的代数和应等于原有受荷的面积；③所画出的每一个矩形面积中，l为长边，b为短边。

3．矩形基底受竖直三角形荷载作用

由于弯矩作用，基底荷载呈梯形分布，此时可采用均匀分布及三角形分布的荷载叠加来计算地基中的附加应力。

图2－24 矩形基底受铅直三角形分布荷载下的竖向附加应力计算

如图2－24所示，在矩形基础底面上作用着三角形分布荷载，最大荷载强度为p0，把荷载强度为零的角点1（或荷载强度为最大的角点2）作为坐标原点，利用积分方法，经简化得角点1（或2）任意深度的竖向附加应力计算公式为

σz＝αc1·p0或 σz＝αc2·p0 　（2－23）

式中：αc1——三角形荷载零角点下的竖向附加应力系数，其值由l／b，z／b查表2－4可得；

αc2——三角形荷载最大值角点下的竖向附加应力基数，其值由l／b，z／b查表2－4可得；

b——三角形荷载分布方向的基础边长。

表2－4 矩形基底受铅直三角形荷载作用下的竖向附加应力系数

续表

续表

4．圆形基底受均布荷载作用

如图2－25所示，地表圆形面积上作用竖直均布荷载p时，荷载中心点下任意深度z处M点的附加应力σz，仍可通过布辛尼斯克解在圆面积内积分求得。

图2－25 圆形基底受铅直均布荷载下中心点的附加应力计算

将极坐标原点放在圆心O处，在荷载面积内取—微分面积d A＝dθdξ，将其上作用的荷载视为集中力dp＝pd A＝pdθdp，dp作用点与M点距离为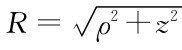，则dp在M点引起的附加应力为，整个圆面积上均布荷载在M点引起的应力，经积分简化为

σz＝α0p 　（2－24）

式中：α0——圆形基础底面受均布荷载作用在中心点下附加应力系数，由z／r0查表2－5可得。

同理，可计算圆形基础底面受均布荷载作用在边下的竖向附加应力为

σr＝αrp 　（2－25）

式中：αr——圆形基础底面受均布荷载作用在边点下竖向附加应力系数，由z／r0查表2－5可得。

表2－5 圆形基础底面受铅直均布荷载作用下的竖向附加应力系数

5．条形基底受铅直均布荷载作用

条形均布荷载下土中应力计算属于平面应变问题，对路堤、堤坝、挡土墙等及长宽比l／b≥10的条形基础均可视为平面应变问题进行处理。

在土体表面分布宽度为b的均布条形荷载p0时，坐标原点O取在条形面积的中点（见图2－26），土中任一点可采用弹性理论中的弗拉曼公式在荷载分布宽度范围内积分得到。

图2－26 条形基底受铅直均布荷载下的竖向附加应力

σz＝αsz·p0 　（2－26）

σx＝αsx·p0 　（2－27）

τzx＝τxz＝αszxp0 　（2－28）

式中：αsz、αsx、αszx——σz、σx、τzx的附加应力系数，可由x／b及z／b查表2－6得出。

表2－6 条形基础底面受均不荷载下的附加应力系数

6．条形基底受竖直三角形分布荷载作用

在基底表面作用三角形分布条形荷载时（见图2－27），其最大值为pt，即坐标原点O取条形基础三角荷载零点线上的基底中任一点。则深度z处的附加应力，仍可利用布辛尼斯克解。

图2－27 条形基底受三角形荷载作用下的竖向附加应力

通过积分得到

σz＝αtzpt 　（2－29）

σx＝αt xpt 　（2－30）

τzx＝αtzxpt 　（2－31）

式中：αtz、αt x、αtzx——σz、σx、τzx的附加应力系数，可由x／b及z／b查表2－7得出。

表2－7 条形基底受铅直三角形分布荷载作用下的附加应力系数

7．地基附加应力的分布规律

图2－28所示为地基中的附加应力等值线图。所谓等值线就是地基中具有相同附加应力数值的点的连线（类似于地形等高线）。由图2－28（a）、（b），地基中的竖向附加应力σz具有如下的分布规律。

（1）σz的分布范围相当大，它不仅分布在荷载面积之内，而且还分布到荷载面积以外，这就是所谓的附加应力扩散现象。

（2）在离基础底面（地基表面）不同深度z处的各个水平面上，以基底中心点下轴线处的σz为最大。离开中心轴线愈远的点，σz愈小。

（3）在荷载分布范围内任意点竖直线上的σz值，随着深度增大逐渐减小。

（4）方形荷载所引起的σz，其影响深度要比条形荷载小得多。例如，在方形荷载中心下z＝2b处，σz≈0．1p0，而在条形荷载下的σz＝0．1p0等值线则约在中心下z＝6b处通过。这一等值线反映了附加应力在地基中的影响范围。在后面某些章节中还会提到地基主要受力层这一概念，它指的是基础底面至σz＝0．2p0深度处（对条形荷载，该深度约为3b，方形荷载约为1．5b）的这部分土层。建筑物荷载主要由地基的主要受力层承担，并且地基沉降的绝大部分是由这部分土层的压缩所形成的。

图2－28 附加应力等值线

（5）当两个或多个荷载距离较近时，扩散到同一区域的竖向附加应力会彼此叠加起来，使该区域的附加应力比单个荷载作用时明显增大。这就是所谓的附加应力叠加现象。

由条形荷载下的σx和τxz的等值线图可知，σx的影响范围较浅，所以基础下地基土的侧向变形主要发生于浅层；而τxz的最大值出现于荷载边缘，所以位于基础边缘下的土容易发生剪切破坏。

由上述分布规律可知，当地面上作用有大面积荷载（或地下水位大范围下降）时，附加应力σz随深度增大而衰减的速率将变缓，其影响深度将会相当大，因此往往会引起可观的地面沉降。当岩层或坚硬土层上可压缩土层的厚度小于或等于荷载面积宽度的一半时，荷载面积下的σz几乎不扩散，此时可认为荷载面中心点下的σz不随深度变化（见图2－29）。

图2－29 可压缩土层厚度h≤0．5b时的σz分布

三、任务实施

【例2－4】 某荷载面为2m×1m，其上竖向均布荷载为p＝100kPa，如图2－30所示。求荷载面上点A、E、O以及荷载面外点F、G等各点下z＝1m深度处的附加应力。并利用计算结果说明附加应力的扩散规律。

图2－30 例2－4图

【解】 （1）A点下的应力。

A点是矩形ABCD的角点，m＝l／b＝2，n＝z／b＝1，由表2－3可得αc＝0．200，故

σz A＝αcp＝0．200×100kPa＝20kPa

（2）E点下的应力。

通过E点将矩形荷载面分为两个相等矩形EADI和EBCI。求EADI的角点的附加应力系数αc。

已知m＝1，n＝1，由表2－3得αc＝0．175，故

σz E＝2αcp＝2×0．175×100kPa＝35kPa

（3）O点下的应力。

通过O点将原矩形面积分为4个相等矩形OEAJ、OJDI、OICK和OKBE，求OEAJ角点的附加应力系数αc。

已知m＝1／0．5＝2，n＝1／0．5＝2，由表2－3得αc＝0．120，故

σz O＝4αcp＝4×0．120×100kPa＝48kPa

（4）F点下的应力。

过F点作矩形FGAJ、FJDH、FGBK和FKCH。

设αcⅠ为矩形FGAJ和FJDH的角点的附加应力系数，αcⅡ为矩形FGBK和FKCH的角点的附加应力系数。

求αcⅠ：已知m＝2．5／0．5＝5，n＝1／0．5＝2，由表2－3得αcⅠ＝0．136；

求αcⅡ：已知m＝0．5／0．5＝1，n＝1／0．5＝2，由表2－3得αcⅡ＝0．084，故

σz F＝2（αcⅠ－αcⅡ）p＝2×（0．136－0．084）×100kPa＝10．4kPa

（5）G点下的应力。

通过G点作矩形GADH和GBCH，分别求出它们的角点的附加应力系数αcⅠ和αcⅡ。

求αcⅠ：已知m＝2．5／1＝2．5，n＝1／1＝1，由表2－3得αcⅠ＝0．201 5；

求αcⅡ：已知m＝1／0．5＝2，n＝1／0．5＝2，由表2－3得αcⅡ＝0．120，故

σz G＝（αcⅠ－αcⅡ）p＝（0．2015－0．120）×100kPa＝8．15kPa

将计算结果绘于图中，可得出附加应力的分布规律。

【例2－5】 某条形基础，其荷载分布如图2－31所示。计算G点下深度为3m处的附加应力σz。

图2－31 例2－5图

【解】 本例求解时需对荷载分布图形进行分解计算，然后叠加。

（1）均布荷载（ABDC）作用，原点为O1（CD段的中心），p＝150kPa。

由x／b＝4／2＝2，z／b＝3／2＝1．5，查表2－6，得αsz＝0．06。

σz1＝0．06×150kPa＝9．0kPa

（2）三角形分布荷载（ACG）作用，原点为O2（CG段的中心），pt＝150kPa

由x／b＝0／3＝0，z／b＝3／3＝1，查表2－7，得αtz＝0．159。

σz2＝0．159×150kPa＝23．85kPa

（3） 　σz＝σz1＋σz2＝（9＋23．85）kPa＝32．85kPa

四、任务小结

附加应力的计算小结见表2－8。地基中附加应力的分布规律为：①距离地面越远，附加应力分布的范围越广；②在地面下任意深度的水平面上，基础中心点下附加应力最大，向四周逐渐减小；③基础中心点下，附加应力随着深度的增加而递减。

表2－8 地基中附加应力计算小结

五、拓展提高

非均质与各向异性地基中的应力计算

前面讨论地基附加应力的计算方法是假定地基土为均质和各向同性的半无限线性空间变形体，然后按照弹性力学理论进行附加应力计算的。而实际上土中应力并非如此，地基土往往是非均质的和各向异性的。在一般情况下按上述方法计算是可行的，但在某些情况下，应用上述应力计算方法得出的结果与实际情况的误差较大。

对非均质与各向异性地基应力计算往往比较复杂，目前对这些类别的土体在荷载作用下的工作机理尚不能建立合理的计算模型。下由对几种特殊地基进行讨论。

1．双层地基

1）上软下硬的地基

在山区地基中，通常基岩埋藏较浅，表层为覆盖的可压缩土层，呈现上软下硬的情况。图2－32所示为这种地基模型，有上软下硬的现象，如图2－32（a）所示。此时，地基土层中的附加应力比均质土上有所增加，即出现应力集中现象。实验表明：岩层埋藏越浅，应力集中的影响越显著，但可压缩土层的厚度小于或等于荷载面积宽度一半时，荷载面积下的附加应力几乎不扩散，此时中点下的附加应力不随深度而变化，如图2－32（b）所示。

图2－32 非均质地基对附加应力的影响

（图中虚线表示均质地基中同一水平面上的附加应力分布）

2）上硬下软的地基

这是一种较常遇到的情况，如图2－33所示。例如，软土地区的地表硬壳层下有着很厚的软弱土层；道路工程中的刚性路面下有一层压缩性较大的土层等。此时，将出现地基中竖向应力分散现象。图2－33所示为均布荷载中心线下竖向应力分布的比较，图中曲线1（虚线）为均质地基中的附加应力的分布图，曲线2为岩层上可压缩土层中的附加应力分布图，而曲线3表示上层坚硬下层软弱的双层地基中的附加应力分布图。

2．变形模量随深度增大的地基

由于地基土层沉积年代的不同，各层土应力值不同，因而各层土的变形模量也不同。即使地基土由单一土层构成，其变形模量E多少存在着随深度逐渐增加的现象。在砂砾土中，这种现象比黏性土更为明显。在此情况下，沿荷载对称轴上的附加应力较各向同性体时增大。一般认为这是由于较深处土的侧向变形受约束所致。应力集中的程度与变形模量E沿深度的变化规律及泊松比有关。弗洛列希（Frohlich）于1942年提出了在集中力作用下垂直附加应力的计算半经验公式。

图2－33 双层地基竖向应力分布的比较

式中：n——应力集中因数。

3．各向异性地基

由于土层生成时各个时期沉积物成分上的变化，土层薄的交互层地基，其水平向变形模量常大于竖向变形模量。与均质各向同性地基相比，此时各水平面上的附加应力的分布将发生扩散现象，即荷载中心线附近的附加应力减少，而远处则增加。沃尔夫（Wolf）于1935年提出，假设地基竖直和水平方向的泊松比相同，得出绝对柔性均布条形荷载中心线下竖直向附加应力计算理论。根据该理论知，在非均质地基中，当水平向变形模量大于竖向变形模量时，地基土中将出现应力集中现象，相反，当水平向变形模量小于竖向变形模量时，地基土中将出现应力分散现象。

威斯特卡德（Westergaard）于1938年假设半空间体内夹有间距极小的且完全柔性的水平薄层，这些薄层只允许产生竖向变形，从而得出了集中荷载P作用下地基中附加应力σz的计算公式如下。

将式（2－33）与布辛尼斯克解相比较，可知它们在形式上有相似之处，其中

式中：μ——柔性薄层的泊松比。

六、拓展练习

1．如图2－34所示，某正方形基础的基底为竖向均布附加压力p＝200kPa，求在正方形中点O、H和G点下深度10m处的附加应力。

图2－34 习题1图

2．如图2－35所示，有一矩形面积（l＝5m，b＝3m）上作用有三角形分布荷载，荷载最大值p＝100kPa，计算在矩形面积O点下z＝3m处M点的竖向附加应力值。

图2－35 习题2图

3．圆形基础上作用着均布荷载p＝40kPa。求基础中点O和边点A下2，4，6和10m深处的αz，并绘出αz沿深度的分布图。

图2－36 习题4图

4．某建筑物为条形基础，宽b＝4m，如图2－36所示。求基底下z＝2m的水平面上，沿宽度方向A、B、C、D点距中心垂线距离分别为0、b／4、b／2、b时，A、B、C、D点的附加应力，并绘出分布曲线。