空间问题的附加应力计算

1.矩形面积受竖向均布荷载作用时的附加应力计算

当竖向均布荷载作用在矩形基础底面时,求基础角点下任意深度处的竖向附加应力,可将坐标原点取在角点O上,在荷载面内取任意微分面积dA＝dx·dy,其上面荷载的合力以集中力dp代替,dp＝pdA＝pdx·dy,然后利用式(3-12)沿着整个矩形面积进行二重积分求得,如图3-12所示。

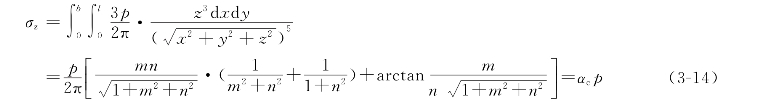
式中 αc——竖向均布荷载作用下矩形基底角点下的竖向附加应力系数,无量纲,是m和n的函数,m＝,n＝,可由表3-2查得。l为基础长边,b为基础短边;z是从基础底面起算的深度;

　　　p——均布荷载强度,求地基附加应力时,用前述基底附加压力p0。

图3-12　矩形面积均布荷载作用时角点下的附加应力

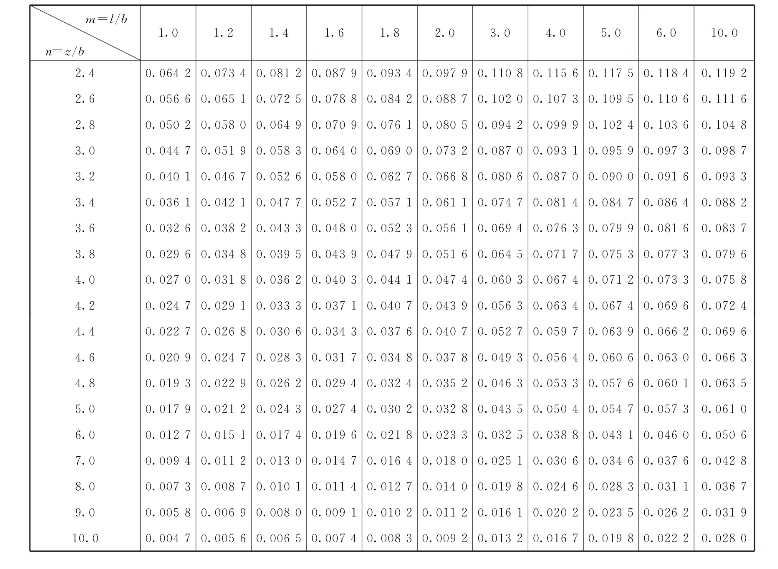
表3-2　矩形面积受竖向均布荷载作用时角点下的附加应力系数αc

续表

对于在基底范围以内或以外任意点下的竖向附加应力,如图3-13所示,求M′点下任意深度处的附加应力时,可过M′点将荷载面积划分为几个小矩形,使M′点成为每个小矩形的共同角点,利用角点下的应力计算式(3-14)分别求出每个小矩形在M′点下同一深度处的附加应力,然后利用叠加原理求得总的附加应力,这种方法称之为“角点法”。

图3-13　角点法的应用

(a)计算矩形荷载面边缘任一点M′之下的附加应力时:

σz＝(αcⅠ＋αcⅡ)p

(b)计算矩形荷载面内任一点M′之下的附加应力时:

σz＝(αcⅠ＋αcⅡ＋αcⅢ＋αcⅣ)p

(c)计算矩形荷载面边缘外任一点M′之下的附加应力时:

σz＝(αcⅠ＋αcⅡ－αcⅢ－αcⅣ)p

(d)计算矩形荷载面角点外侧任一点M′之下的附加应力时:

σz＝(αcⅠ－αcⅡ－αcⅢ＋αcⅣ)p

以上各式中αcⅠ、αcⅡ、αcⅢ、αcⅣ分别为矩形M′hbe、M′fce、M′hag、M′fdg的角点应力分布系数。

应用“角点法”时,要注意:①划分矩形时,M′点应为公共角点;②所有划分的矩形总面积应等于原有受荷面积;③每一个矩形面积中,长边为l,短边为b。

【例3-4】 均布荷载P＝100kN/m2,荷载面积为(2×1)m2,如图3-14所示,求荷载面积上角点A、边点E、中心点O以及荷载面积外F点和G点等各点下z＝1m深度处的附加应力。

图3-14　荷载计算图

【解】 (1)A点下的附加应力。A点是矩形ABCD的角点,且m＝l/b＝2/1＝2;n＝z/b＝1,查表3-5得

αc＝0.1999,故σzA＝αc·P＝0.1999×100≈20(kN/m2)

(2)E点下的附加应力。通过E点将矩形荷载面积划分为两个相等的矩形EADI和EBCI。求EADI的角点应力系数αc:m＝1,n＝1;查表得αc＝0.1752,故

σzE＝2αc·P＝2×0.1752×100≈35(kN/m2)

(3)O点下附加应力。通过O点将原矩形面积分为4个相等的矩形OEAJ、OJDI、OICK和OKBE。求矩形OEAJ角点的附加应力系数αc:

查表得αc＝0.1202,故σzO＝4αc·p＝4×0.1202×100＝48.1(kN/m2)

(4)F点下附加应力。过F点作矩形FGAJ、FJDH、FGBK和FKCH。假设αcⅠ为矩形FGAJ和FJDH的角点应力系数;αcⅡ为矩形FGBK和FKCH的角点应力系数。

故σzF＝2(αcⅠ－αcⅡ)P＝2×(0.1363－0.0840)×100＝10.5(kN/m2)

(5)G点下附加应力。通过G点作矩形GADH和GBCH分别求出它们的角点应力系数αcⅠ和αcⅡ。

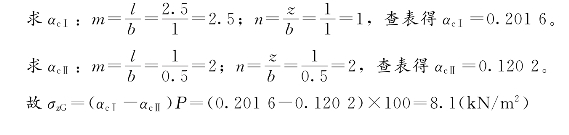
2.矩形面积受竖向三角形分布荷载作用时的附加应力计算

竖向三角形分布荷载作用在矩形基底时,若矩形基底上三角形的最大荷载强度为pt,把荷载强度为零的角点O(角点1)作为坐标原点,则微分面积dxdy上的作用力dp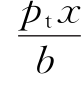＝dxdy可作为集中力看待,如图3-15所示,同样可利用公式σz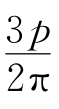＝·沿着整个面积进行二重积分求解角点O(角点1)下任意深度z处的竖向附加应力为:

图3-15　矩形面积三角形分布荷载作用时角点下的附加应力

式中,αt1＝为矩形基底受竖向三角形分布荷载作用时角点1(荷载强度为零的角点)下的竖向附加应力系数,可由(m＝bl ,n＝bz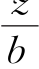) 查表3-3求得,其中,b是三角形荷载分布方向的边长。

同理,荷载强度最大边的角点2下任意深度z处的附加应力为:

式中,αt2为矩形基底受竖向三角形分布荷载作用时角点2(荷载强度最大边的角点)下的竖向附加应力系数,可由(m＝,n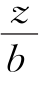＝)查表3-3求得。

表3-3　矩形面积受竖直三角形分布荷载作用时角点下的竖向附加压力系数αt1、αt2

续表

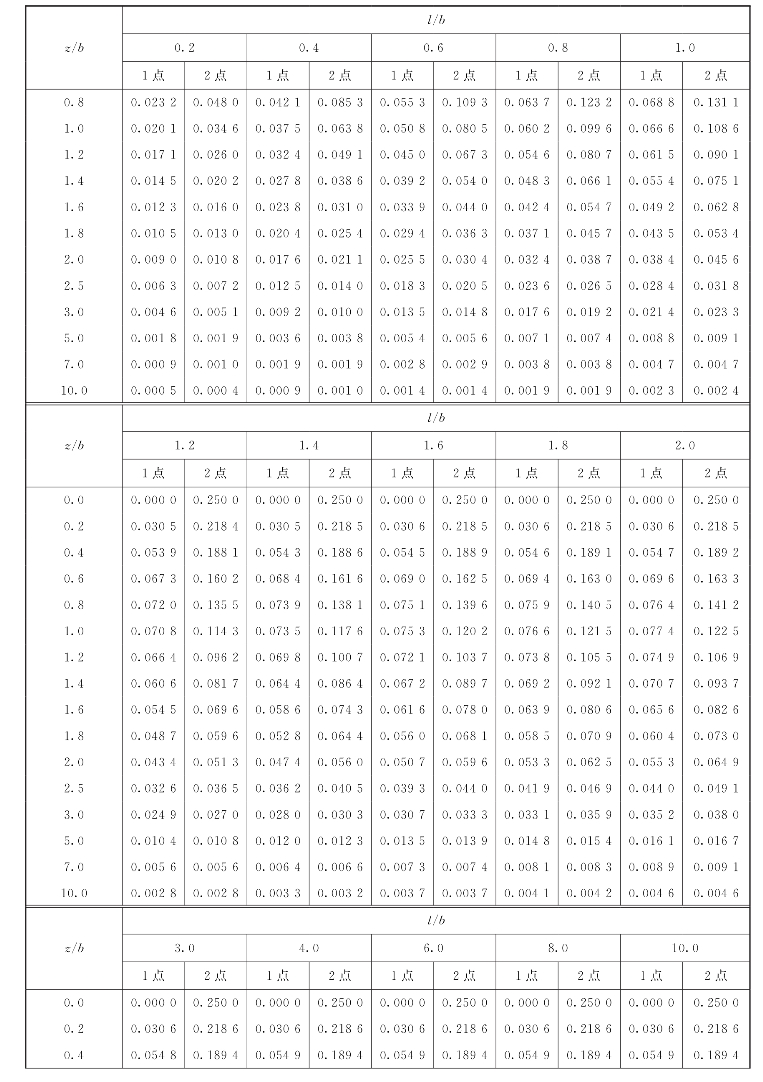
续表

应用均布和三角形分布荷载的角点公式及叠加原理,可以求得矩形面积上的三角形和梯形荷载作用下地基内任意一点的附加应力。

3.4.3 平面问题的附加应力计算

当一定宽度的无限长条面积承受均布荷载时,在土中垂直于长度方向的任一截面附加应力分布规律均相同,且在长条延伸方向的地基的应变和位移均为0,这类问题称为平面问题。实际建筑中并没有无限长的荷载面积,研究表明,当基础的长度比l/b≥10时,计算的地基附加应力值与按l/b＝∞时的解相差甚微,因此,墙基、路基、挡土墙基础等均可按平面问题计算地基中的附加应力。对此类问题,只要算出任一截面上的附加应力,即可代表其他平行截面。

1.均布竖向线荷载

当竖向均布线荷载p作用于地表面时,在线荷载上取微分长度dy,作用在上面的荷载pdy可看做集中力,如图3-16所示,则在地基内M点引起的附加应力为dσz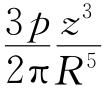＝dy。

通过积分可求得均布竖向线荷载p作用下地基中任意点M的附加应力为:

该解答由弗拉曼首先得到,故称弗拉曼解,实际意义上的线荷载是不存在的,可以将其看作是条形面积在宽度趋于零时的特殊情况,以该解答为基础,通过积分可求解各类平面问题地基中的附加应力。

2.均布竖向条形荷载

当宽度为b的条形基础上作用有均布荷载p时,取宽度b的中点为坐标原点,如图3-17所示,则地基中某点的竖向附加应力可由式(3-17)在荷载分布宽度b范围内进行积分求得:

图3-16　均布竖向线荷载作用下地基附加应力

图3-17　均布竖向条形荷载作用下地基附加应力

式中 αs——条形基础上作用竖向均布荷载时的竖向附加应力系数,由(m＝x/b,n＝z/b)查表3-4可得。

表3-4　均布竖向条形荷载作用下的附加应力系数αs