二阶线性微分方程的一般形式为  其中
其中 都是一次的,否则称为二阶非线性方程,其中
都是一次的,否则称为二阶非线性方程,其中 均为连续函数。当右端
均为连续函数。当右端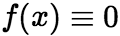 ,方程叫做齐次的;当右端
,方程叫做齐次的;当右端![]() 不恒等于0,方程叫做非齐次的。
不恒等于0,方程叫做非齐次的。
设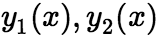 是定义在区间
是定义在区间![]() 的两个函数,如果
的两个函数,如果 (常数),那么称此两函数在区间
(常数),那么称此两函数在区间![]() 线性相关,否则,称此两函数线性独立或线性无关。
线性相关,否则,称此两函数线性独立或线性无关。
(3/13) 线性微分方程的解的结构
1)齐次线性方程解的结构 先讨论二阶线性齐次方程  定理:如果函数
定理:如果函数 均是方程
均是方程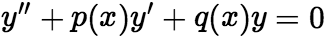 的解,那么
的解,那么 也是该方程的解,其中
也是该方程的解,其中![]() 为任意常数。 定理:如果函数
为任意常数。 定理:如果函数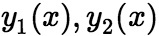 是二阶齐次线性方程的任意两个线性无关的特解,那么
是二阶齐次线性方程的任意两个线性无关的特解,那么 就是该方程的通解,其中
就是该方程的通解,其中![]() 为任意常数。 推论:如果
为任意常数。 推论:如果 是
是 阶齐次线性方程
阶齐次线性方程 
 的
的 个线性无关的解,那么,此方程的通解为
个线性无关的解,那么,此方程的通解为  其中
其中 为任意常数。 (2)非齐次线性方程解的结构 二阶非齐次线性方程的形式为:
为任意常数。 (2)非齐次线性方程解的结构 二阶非齐次线性方程的形式为:  定理:设
定理:设 是二阶非齐次线性方程
是二阶非齐次线性方程 的任一特解,
的任一特解, 是与该方程对应的齐次线性方程
是与该方程对应的齐次线性方程 的通解,那么
的通解,那么 就是方程
就是方程 的通解。 定理:设有非齐次线性方程
的通解。 定理:设有非齐次线性方程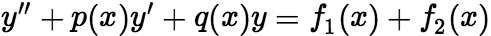 .如果
.如果 分别是方程
分别是方程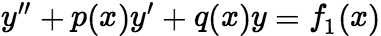 与方程
与方程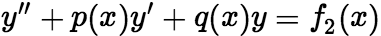 的解,那么
的解,那么 就是原方程的解。
就是原方程的解。
(4/13) 常系数线性齐次方程
(1)二阶常系数齐次线性微分方程 二阶常系数齐次线性方程的一般形式为 ,其中
,其中![]() ,
,![]() 为实常数,其特征方程为
为实常数,其特征方程为 。 依据判别式的符号,其通解有三种形式: (i)当
。 依据判别式的符号,其通解有三种形式: (i)当 ,特征方程有两个相异的实根
,特征方程有两个相异的实根![]() ,通解的形式为
,通解的形式为  (ii)当
(ii)当 ,特征方程有重根,即
,特征方程有重根,即 ,通解的形式为
,通解的形式为 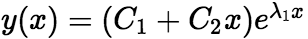 (iii)当
(iii)当 ,特征方程有共轭复根重根
,特征方程有共轭复根重根![]() ,通解的形式为
,通解的形式为  (2)
(2)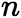 阶常系数齐次线性微分方程
阶常系数齐次线性微分方程  阶常系数齐次线性方程的一般形式为
阶常系数齐次线性方程的一般形式为  , 其中
, 其中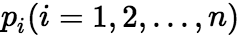 为常数,相应的特征方程为
为常数,相应的特征方程为 。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若
。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若 是
是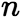 个相异实根,则原方程的通解为
个相异实根,则原方程的通解为 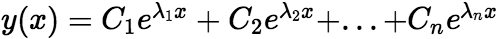 (ii)若
(ii)若![]() 为特征方程的
为特征方程的 重实根,则原方程的通解中含有
重实根,则原方程的通解中含有  (iii)若
(iii)若![]() 为特征方程的
为特征方程的 重共轭复根,则原方程的通解中含有
重共轭复根,则原方程的通解中含有 

(5/13) 二阶常系数线性非齐次方程
二阶常系数线性非齐次方程的一般形式为 ,其中
,其中![]() 为实常数。由于非齐次线性方程的通解,等于它的任一特解与对应齐次线性方程的通解之和。根据f(x)具有下列特殊情形时,来给出求其特解的公式: (1)
为实常数。由于非齐次线性方程的通解,等于它的任一特解与对应齐次线性方程的通解之和。根据f(x)具有下列特殊情形时,来给出求其特解的公式: (1)  ,
,![]() 为
为 次多项式 特解形式分为三种情况: (i)0不是特征根:
次多项式 特解形式分为三种情况: (i)0不是特征根: (ii)0是特征方程的单根:
(ii)0是特征方程的单根: (iii)0是特征方程的重根:
(iii)0是特征方程的重根: (2)
(2)  ,
,![]() 为
为 次多项式 特解形式分为三种情况: (i)
次多项式 特解形式分为三种情况: (i)![]() 不是特征根:
不是特征根: (ii)
(ii)![]() 是特征方程的单根:
是特征方程的单根: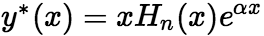 (iii)
(iii)![]() 是特征方程的重根:
是特征方程的重根: (3)
(3)  ,
,  为
为 次,
次,![]() 次多项式 特解形式分为两种情况: (i)
次多项式 特解形式分为两种情况: (i)![]() 不是特征根:
不是特征根: (ii)
(ii)![]() 是特征根:
是特征根: 其中
其中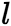 次多项式
次多项式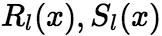 中的
中的 。 (4)
。 (4)  ,特解:
,特解:
(6/13) 欧拉方程
形如
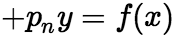 的方程(其中
的方程(其中 为常数),叫做欧拉方程。作代换
为常数),叫做欧拉方程。作代换 ,即可将原方程化为
,即可将原方程化为 阶常系数线性微分方程。 特别的,对于二阶欧拉方程
阶常系数线性微分方程。 特别的,对于二阶欧拉方程  令
令 


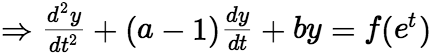 即化成了二阶线性常微分方程。
即化成了二阶线性常微分方程。
(7/13) 二阶常系数线性齐次方程
二阶常系数齐次线性微分方程 二阶常系数齐次线性方程的一般形式为 ,其中
,其中![]() ,
,![]() 为实常数,其特征方程为
为实常数,其特征方程为 。 依据判别式的符号,其通解有三种形式: (i)当
。 依据判别式的符号,其通解有三种形式: (i)当 ,特征方程有两个相异的实根
,特征方程有两个相异的实根![]() ,通解的形式为
,通解的形式为  (ii)当
(ii)当 ,特征方程有重根,即
,特征方程有重根,即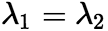 ,通解的形式为
,通解的形式为  (iii)当
(iii)当 ,特征方程有共轭复根重根
,特征方程有共轭复根重根![]() ,通解的形式为
,通解的形式为 
(8/13) 二阶线性微分方程的定义
二阶线性微分方程的一般形式为  其中
其中 都是一次的,否则称为二阶非线性方程,其中
都是一次的,否则称为二阶非线性方程,其中 均为连续函数。当右端
均为连续函数。当右端 ,方程叫做齐次的;当右端
,方程叫做齐次的;当右端![]() 不恒等于0,方程叫做非齐次的。
不恒等于0,方程叫做非齐次的。
(9/13) 函数的线性相关与线性独立的定义
设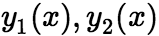 是定义在区间
是定义在区间![]() 的两个函数,如果
的两个函数,如果 (常数),那么称此两函数在区间
(常数),那么称此两函数在区间![]() 线性相关,否则,称此两函数线性独立或线性无关。
线性相关,否则,称此两函数线性独立或线性无关。
(10/13) 线性微分方程的解的结构
1)齐次线性方程解的结构 先讨论二阶线性齐次方程  定理:如果函数
定理:如果函数 均是方程
均是方程 的解,那么
的解,那么 也是该方程的解,其中
也是该方程的解,其中![]() 为任意常数。 定理:如果函数
为任意常数。 定理:如果函数 是二阶齐次线性方程的任意两个线性无关的特解,那么
是二阶齐次线性方程的任意两个线性无关的特解,那么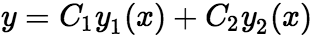 就是该方程的通解,其中
就是该方程的通解,其中![]() 为任意常数。 推论:如果
为任意常数。 推论:如果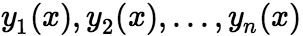 是
是 阶齐次线性方程
阶齐次线性方程 
 的
的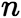 个线性无关的解,那么,此方程的通解为
个线性无关的解,那么,此方程的通解为 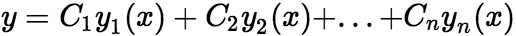 其中
其中 为任意常数。 (2)非齐次线性方程解的结构 二阶非齐次线性方程的形式为:
为任意常数。 (2)非齐次线性方程解的结构 二阶非齐次线性方程的形式为:  定理:设
定理:设 是二阶非齐次线性方程
是二阶非齐次线性方程 的任一特解,
的任一特解, 是与该方程对应的齐次线性方程
是与该方程对应的齐次线性方程 的通解,那么
的通解,那么 就是方程
就是方程 的通解。 定理:设有非齐次线性方程
的通解。 定理:设有非齐次线性方程 .如果
.如果 分别是方程
分别是方程 与方程
与方程 的解,那么
的解,那么 就是原方程的解。
就是原方程的解。
(11/13) 常系数线性齐次方程
(1)二阶常系数齐次线性微分方程 二阶常系数齐次线性方程的一般形式为 ,其中
,其中![]() ,
,![]() 为实常数,其特征方程为
为实常数,其特征方程为 。 依据判别式的符号,其通解有三种形式: (i)当
。 依据判别式的符号,其通解有三种形式: (i)当 ,特征方程有两个相异的实根
,特征方程有两个相异的实根![]() ,通解的形式为
,通解的形式为  (ii)当
(ii)当 ,特征方程有重根,即
,特征方程有重根,即 ,通解的形式为
,通解的形式为 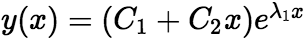 (iii)当
(iii)当 ,特征方程有共轭复根重根
,特征方程有共轭复根重根![]() ,通解的形式为
,通解的形式为  (2)
(2) 阶常系数齐次线性微分方程
阶常系数齐次线性微分方程  阶常系数齐次线性方程的一般形式为
阶常系数齐次线性方程的一般形式为  , 其中
, 其中 为常数,相应的特征方程为
为常数,相应的特征方程为 。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若
。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若 是
是 个相异实根,则原方程的通解为
个相异实根,则原方程的通解为  (ii)若
(ii)若![]() 为特征方程的
为特征方程的 重实根,则原方程的通解中含有
重实根,则原方程的通解中含有  (iii)若
(iii)若![]() 为特征方程的
为特征方程的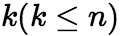 重共轭复根,则原方程的通解中含有
重共轭复根,则原方程的通解中含有 

(12/13) 常系数线性齐次方程
(1)二阶常系数齐次线性微分方程 二阶常系数齐次线性方程的一般形式为 ,其中
,其中![]() ,
,![]() 为实常数,其特征方程为
为实常数,其特征方程为 。 依据判别式的符号,其通解有三种形式: (i)当
。 依据判别式的符号,其通解有三种形式: (i)当 ,特征方程有两个相异的实根
,特征方程有两个相异的实根![]() ,通解的形式为
,通解的形式为  (ii)当
(ii)当 ,特征方程有重根,即
,特征方程有重根,即 ,通解的形式为
,通解的形式为  (iii)当
(iii)当 ,特征方程有共轭复根重根
,特征方程有共轭复根重根![]() ,通解的形式为
,通解的形式为  (2)
(2)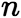 阶常系数齐次线性微分方程
阶常系数齐次线性微分方程  阶常系数齐次线性方程的一般形式为
阶常系数齐次线性方程的一般形式为  , 其中
, 其中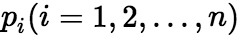 为常数,相应的特征方程为
为常数,相应的特征方程为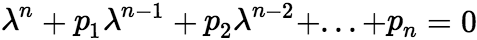 。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若
。特征根与通解的关系同二阶方程的情形类似,具体结论如下: (i)若 是
是 个相异实根,则原方程的通解为
个相异实根,则原方程的通解为  (ii)若
(ii)若![]() 为特征方程的
为特征方程的 重实根,则原方程的通解中含有
重实根,则原方程的通解中含有  (iii)若
(iii)若![]() 为特征方程的
为特征方程的 重共轭复根,则原方程的通解中含有
重共轭复根,则原方程的通解中含有 

(13/13) 二阶常系数线性非齐次方程
二阶齐次线性方程的一般形式为 ,其中
,其中![]() 为实常数。由于非齐次线性方程的通解,等于它的任一特解与对应齐次线性方程的通解之和。根据f(x)具有下列特殊情形时,来给出求其特解的公式: (1)
为实常数。由于非齐次线性方程的通解,等于它的任一特解与对应齐次线性方程的通解之和。根据f(x)具有下列特殊情形时,来给出求其特解的公式: (1)  ,
,![]() 为n次多项式 特解形式分为三种情况: (i)0不是特征根:
为n次多项式 特解形式分为三种情况: (i)0不是特征根: (ii)0是特征方程的单根:
(ii)0是特征方程的单根: (iii)0是特征方程的重根:
(iii)0是特征方程的重根: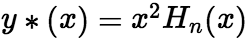 (2)
(2)  ,
,![]() 为n次多项式 特解形式分为三种情况: (i)
为n次多项式 特解形式分为三种情况: (i)![]() 不是特征根:
不是特征根: (ii)
(ii)![]() 是特征方程的单根:
是特征方程的单根: (iii)
(iii)![]() 是特征方程的重根:
是特征方程的重根: (3)
(3) 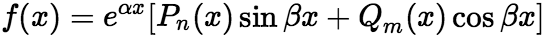 ,
,  为n次,m次多项式 特解形式分为二种情况: (i)
为n次,m次多项式 特解形式分为二种情况: (i)![]() 不是特征根:
不是特征根: (ii)
(ii)![]() 是特征根:
是特征根: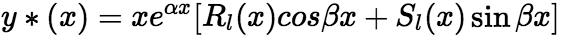 其中
其中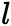 次多项式
次多项式 中
中 。 (4)
。 (4)  , 特解:
, 特解: 例5 求下列微分方程 (1)
例5 求下列微分方程 (1) (2)
(2) 解:(1)
解:(1) (2)
(2)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















