求函数区间上的断点

自然界中连续变化的现象是很多的，如空气或水的流动，气温的变化等．这些现象反映到数学的函数关系上就是函数的连续性．函数的连续性是微积分学的基本概念之一，它同函数的极限概念有密切的联系．

定义1　设函数f（x）在点x0的某个领域内有定义，如果

则称函数f（x）在点x0处连续，并称点x0为f（x）的连续点．

例如，函数f（x）＝2x＋1在点x＝2连续，这是因为

又如函数

在点x＝0连续，这是因为

由于函数f（x）在点x0处连续是用极限来定义的，故f（x）在点x0处连续可用ε－δ语言描述如下：

设函数f（x）在点x0的某个领域内有定义，如果对当｜x－x0｜＜δ时，就有

｜f（x）－f（x0）｜＜ε，

则称函数f（x）在点x0处连续．

为了介绍函数f（x）在点x0处连续的另一种表述，需要给出变量的增量的概念．

称x－x0为自变量x在x0处的增量（或改变量），记为Δx，即

Δx＝x－x0．

对应函数值的差f（x）－f（x0）称为函数f（x）在x0处的增量（或改变量），记为Δy，即

Δy＝f（x）－f（x0）＝f（x0＋Δx）－f（x0）．

因为x→x0等价于Δx→0，故定义1中的式（1）等价于

这样，函数y＝f（x）在点x0处连续又可用下述方式定义：

定义2　设函数f（x）在点x0的某个领域内有定义，如果

则称函数y＝f（x）在点x0处连续．

相应于左右极限的概念，给出左右连续的定义．

定义3　设函数f（x）在（x0，x0＋h）（h＞0）（或（x0－h，x0））内有定义，如果

则称函数f（x）在点x0右连续（或左连续）．

据上述定义1与定义3，不难推出如下定理．

定理1　函数f（x）在点x0处连续的充要条件是：f（x）在点x0处既是右连续，又左连续．

例1　讨论函数

在点x＝0的连续性．

解　因为

而f（0）＝2，所以f（x）在点x＝0右连续，但不左连续，故它在x＝0不连续．

如果函数f（x）在区间I上的每一点都连续，则称f（x）为该区间上的连续函数，并称I为f（x）的连续区间．

若区间I包含端点，在左端点处连续是指右连续，在右端点处连续是指左连续．

直观上，连续函数的图形是一条连绵不断的曲线．

例如，函数y＝c，y＝x，y＝sin x和y＝cos x都是R上的连续函数．又如函数在（－1，1）内每一点处都连续，在x＝1处为左连续，在x＝－1处为右连续，因而它在［－1，1］上连续．

定义4　设函数f（x）在x0的某个去心邻域内有定义．如果f（x）在点x0处不连续，则称点x0为函数f（x）的不连续点或间断点．

下面对函数的间断点进行分类讨论．

例如，函数f（x）＝｜sgn x｜，因f（0）＝0，而

故x＝0为f（x）＝｜sgnx｜的可去间断点．但改变定义，令f（0）＝1，则函数在x＝0处连续．

所以x＝0是g（x）的可去间断点．但补充定义，令g（0）＝1，则函数在x＝0处连续．

例如，函数f（x）＝sgn x，因为

故x＝0是sgn x的跳跃间断点．从图1.14上看，函数在x＝0处有一个跳跃现象．

图1.14

函数的可去间断点和跳跃间断点统称为第一类间断点．其特点是函数的左、右极限都存在．

除第一类间断点外，所有其他形式的间断点，都称为函数的第二类间断点．其特点是函数的左、右极限至少有一个不存在．

图1.15

由函数连续的定义和极限的四则运算法则，有如下定理：

定理2（四则运算）　若函数f（x），g（x）在点x0连续，则

也都在点x0处连续．

定理3（复合函数的连续性）　如果函数u＝g（x）在点x0连续，y＝f（u）在点u0＝g（x0）连续，则复合函数y＝f［g（x）］在点x0连续．

证　对任给的ε＞0，由于f（x）在u0连续，故存在δ1＞0，使得当｜u－u0｜＜δ1时，有

｜f（u）－f（u0）｜＜ε；

又因为u0＝g（x0），u＝g（x）在点x0连续，故对上述δ1＞0，存在δ＞0，使得当｜x－x0｜＜δ时，有

故对任给的ε＞0，存在δ＞0，当｜x－x0｜＜δ时，有

所以y＝f［g（x）］在点x0连续．

根据连续性的定义，上述定理的结论可表述为

定理4（反函数的连续性）　单调连续函数的反函数也是单调连续的．

例如，y＝sin x在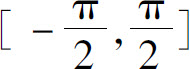上单调连续，故其反函数y＝arcsin x在［－1，1］上单调连续．同理可得其他反三角函数也在相应的定义区间上连续．

解　函数y＝sin（1－x2）可看成函数y＝sin u与u＝1－x2的复合函数，而函数sin u和1－x2连续，故

例3　计算

解

基本初等函数在它们的定义域上都是连续的．

由于任何初等函数都是由基本初等函数经过有限次的四则运算与复合运算所得到，所以有结论：初等函数在其有定义区间上都是连续的．所谓定义区间，就是包含在定义域内的区间．

根据上面这个结论，对于初等函数f（x），如果x0是f（x）的定义区间内的点，则

解

例5　计算

解　由对数函数的连续性有

在闭区间上连续的函数有几个重要性质，我们不加证明地给予介绍．

定义5　设函数f（x）在实数集D上有定义，如果存在x0∈D，使得对一切x∈D有

f（x0）≥f（x）（或f（x0）≤f（x）），

则称f（x0）为f（x）在D上的最大值（或最小值）．

例如，sin x在［0，π］上最大值为1，最小值为0．但一般而言，函数f（x）在定义域D上不一定有最大值或最小值（即使f（x）在D上有界）．如f（x）＝x在（0，1）上有界，但既无最大值也无最小值．

定理5（最值定理）　如果函数f（x）在闭区间［a，b］上连续，则f（x）在［a，b］上有最大值与最小值．

推论　若函数f（x）在闭区间［a，b］上连续，则f（x）在［a，b］上有界．

定理6（介值定理）　设函数f（x）在闭区间［a，b］上连续，且f（a）≠f（b）．若μ为介于f（a）与f（b）之间的任意一个数，即

f（a）＜μ＜f（b）或f（a）＞μ＞f（b），

则至少存在一点ξ∈（a，b），使得

f（ξ）＝μ．

推论1（零点定理）　若函数f（x）在闭区间［a，b］上连续，且f（a）与f（b）异号（即f（a）·f（b）＜0），则至少存在一点ξ∈（a，b）使得

f（ξ）＝0．

从几何上看，推论1表示：如果连续曲线弧y＝f（x），x∈［a，b］的两个端点分别位于x轴的上下两侧，则这段曲线与x轴至少有一个交点，如图1.16所示．

图1.16

推论2　在闭区间上连续的函数必取得介于其最小值m与最大值M之间的任何值．

例6　证明方程x3－5x2＋2＝0在区间（0，1）内至少有一个根．

证　设函数f（x）＝x3－5x2＋2，则f（x）在闭区间［0，1］上连续，且

f（0）＝2＞0，f（1）＝－2＜0．

根据零点定理，在（0，1）内至少存在一点ξ，使得

f（ξ）＝0，

即

ξ3－5ξ2＋2＝0（0＜ξ＜1），

故方程x3－5x2＋2＝0在（0，1）内至少有一个根．

f（0）＝－1＜0，f（1）＝e＋sin 1－2＞0．

根据零点定理，在（0，1）内至少存在一点ξ，使得

f（ξ）＝0，

即

eξ＋sinξ＝2，

1．指出下列函数的间断点并说明其类型：

（3）f（x）＝sgn｜x｜；

（4）f（x）＝sgn（cos x）；

2．问a为何值时，函数

在点x＝1处连续？

3．讨论复合函数f［g（x）］与g［f（x）］的连续性，设

（1）f（x）＝sgn x，g（x）＝1＋x2；

（2）f（x）＝sgn x，g（x）＝（1－x2）x．

4．求极限：

（3）

（4）

（6）

5．证明：若f（x）在［a，b］上连续，且对任何x∈［a，b］，f（x）≠0，则f（x）在［a，b］上恒正或恒负．