有限闭区间上的连续函数

函数连续的概念是按点定义的，可以说是一种局部或微观的性质。如果函数在一个有限闭区间上连续，我们可以得到整体或宏观的信息，它们具有一些非常重要的性质，在理论上有很多应用。

定理2.4.1（有界性定理）　如果f在闭区间［a,b］上连续，则f在［a,b］上有界。

证明　采取反证法。假设f在［a,b］上没有上界，则任取x₁∈［a,b］，存在x₂∈［a,b］使得f（x₂）≥f（x₁）＋1．我们可以归纳地选出［a,b］中的数列｛x_n｝使得对于每一个n，

f（x_n＋1）≥f（x_n）＋1．

由于｛x_n｝是［a,b］中的数列，因此是有界的。由Bolzano-Weierstrass定理（定理1.3.3），｛x_n｝有收敛的子列｛x_nk｝，设则x₀∈［a,b］．

根据f的连续性，

但是

f（x_nk＋1）－f（x_nk）≥n_k＋1－n_k≥1

｛f（x_nk）｝不可能收敛，矛盾。

如果f没有下界，我们可以找到［a,b］中的数列｛x_n｝满足

f（x_n＋1）≤f（x_n）－1．

用类似的方法得到矛盾。

所以f在［a,b］上有界。　　□

我们需要强调的是：有限开区间上的连续函数不一定有界，如在（0,1）上连续，但显然是无界的。

定义2.4.2　设如果存在x₀∈D使得对于任何x∈D，

f（x）≤f（x₀）（或者f（x）≥f（x₀）），

则称f在D上能取到最大（或者最小）值。此时，f（x₀）是f在D上的最大（或者最小）值。

定理2.4.3（最值定理）　设函数f在［a,b］上连续，则f在［a,b］上能取到最大值和最小值。

证明　由定理2.4.1，Y＝f（［a,b］）＝｛f（x）｜x∈［a,b］｝是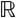的有界子集。由确界原理，Y有上确界和下确界，记为M＝supY，m＝infY．

由于上确界是最小的上界，对于任何n≥1，不是Y的上界，因此存在x_n∈［a,b］使得

｛x_n｝是有界数列，由Bolzan-Weierstrass定理，｛x_n｝存在收敛子列｛x_nk｝，记则d∈［a,b］．

根据f的连续性，

而

令k→＋∞，由夹逼定理，

所以，存在d∈［a,b］使得f（d）＝M，f在［a,b］上能取到最大值。

利用相同的办法可以证明，存在c∈［a,b］使f（c）＝m，f在［a,b］能取到最小值。

□

定理2.4.3对于开区间不成立，如f（x）＝x在（0,1）上连续，但取不到最大值和最小值。

定理2.4.4（零点定理）　设函数f在［a,b］上连续且f（a）f（b）＜0，则存在ξ∈（a,b）使得f（ξ）＝0．

图2.4

证明　不妨设f（a）＜0，f（b）＞0．考虑集合

A＝｛x｜x∈［a,b］,f（x）≤0｝．

因为a∈A，A是非空有界集合。根据确界原理，A有上确界，记为ξ＝supA，则ξ∈（a,b）．我们要证明f（ξ）＝0．

假设f（ξ）＜0．由f的连续性，对于ε＝－f（ξ）＞0，存在δ＞0，当x∈N（ξ,δ）时，

｜f（x）－f（ξ）｜＜ε．

即

f（ξ）－ε＜f（x）＜f（ξ）＋ε＝0．

因此，N（ξ,δ）⊂A，与ξ是A的上确界矛盾。

假设f（ξ）＞0．对于ε＝f（ξ）＞0，存有δ＞0，当x∈N（ξ,δ）时，

｜f（x）－f（ξ）｜＜ε，

即

0＝f（ξ）－ε＜f（x）＜f（ξ）＋ε．

因此，N（ξ,δ）∩A＝⌀，与ξ是A的上确界矛盾。　　□

零点定理在直观上很容易理解，就像从海底走到山顶一定要经过水平线。下面的定理说，如果想从二楼走到四楼，则一定要经过三楼。

定理2.4.5（介值定理）　设函数f在［a,b］上连续，则对于任何η∈［m,M］，存在ξ∈［a,b］使得f（ξ）＝η，其中

m＝inf｛f（x）｜x∈［a,b］｝，M＝sup｛f（x）｜x∈［a,b］｝．

证明　如果f是常值函数，结论显然成立。

假设f不是常值函数，则M＞m．由最值定理，存在c，d∈［a,b］使得f（c）＝m，f（d）＝M．

对于任何η∈（m,M），F（x）＝f（x）－η是［c,d］（或者［d,c］）上的连续函数且F（c）＝m－η＜0，F（d）＝M－η＞0，由零点定理，存在ξ∈［c,d］⊂［a,b］，使得

我们还可以得定理2.4.5用另一种形式表述。

定理2.4.5′　设函数f在［a,b］上连续，则f（［a,b］）＝［m,M］是有限闭区间，其中M和m是f在［a,b］上的最大值和最小值。

注2.4.6　定理2.4.5′可以推广到一般区间。设f是区间I上的连续函数，则f（I）也是一个区间。利用介值定理不难证明这个结论，我们留给读者作为练习。

由零点定理（定理2.4.4），我们可以得到一维的不动点定理。

定理2.4.7　设f∶［a,b］→［a,b］是连续函数，则存在c∈［a,b］使得f（c）＝c（称c是f的不动点）。

证明　考虑函数F（x）＝f（x）－x，则

F（a）＝f（a）－a≥0，F（b）＝f（b）－b≤0．

如果F（a）＝0或者F（b）＝0，则定理得证。

假设F（a）＞0且F（b）＜0，由零点定理，存在c∈（a,b）使得F（c）＝0，即

一维的不动点定理在1910左右，由荷兰数学家L. E. Brouwer（布劳威尔）推广到高维方体上，被称为Brouwer不动点定理，它可广泛应用于证明方程解的存在性。随着现代数学的发展，Brouwer不动点定理被推广为更为广泛的情况而得到许多重要的应用，不动点定理成为近代数学的一个重要研究方向。