§8.4 欧拉积分·广义积分的计算
广义积分的计算除了利用定积分的一些常用方法如牛顿-莱布尼兹公式、换元法、分部积分法、递推法以外,还有许多极富特色的独到的解法。本节在介绍欧拉积分的同时,着重讲解一些特殊的广义积分的计算方法。
一、欧拉积分之Γ函数
2.Γ函数的其他形式
(1)在定义式(1)中,令x=y2得
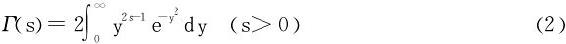
(2)在定义式(1)中,令z=e-x得
3.递推关系 
只要知道Γ(s)在0<s≤1上的值,即可得所有的Γ(s)值。甚至可以据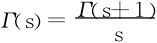 将Γ(s)定义域推广到集合
将Γ(s)定义域推广到集合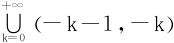 上去。
上去。
二、欧拉积分之Β函数
1.定义式 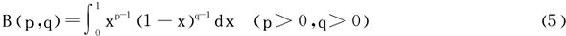
2.B函数的其他形式
(1)在定义式(5)中,令x=sin2θ得
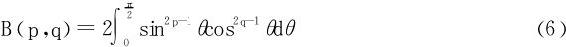

对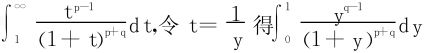
所以又有

3.递推关系
当p>0,q>1时,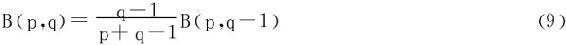
证明 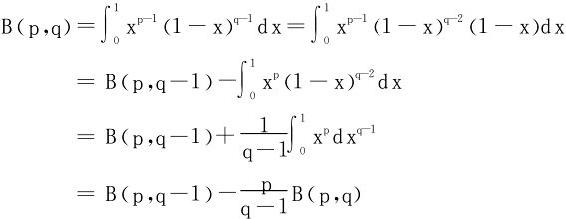
移项立得。
当p>1,q>1时,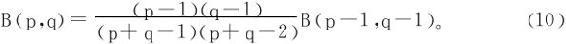
据此,只要知道B(p,q)在0<p≤1;0<q≤1上的值,即可得所有的B(p,q)的值。
三、B函数和Γ函数的转换关系
四、Γ函数余元公式
当0<α<1时,有

如何计算积分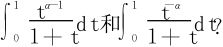 利用幂级数展开:
利用幂级数展开:
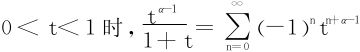
当0<x<1时,在区间[0,x]上可逐项求积分
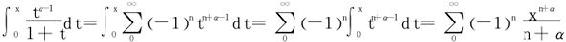
右边级数在x=1处收敛,令x=1,又得:
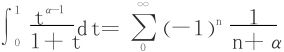
(参见[7]下册第十四章§1习题3,上面推导亦可以直接在[0,x]逐项积分)
类似地:
于是
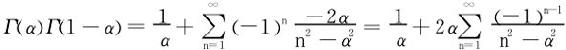
另一方面,据cosαx的Fourier级数展开式:
令x=0得出:
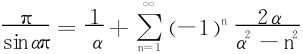
从而得出余元公式
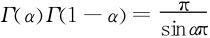
五、Γ函数的欧拉-高斯表示
本段我们将介绍一个非常有趣的公式,即Γ函数的欧拉-高斯表示公式:
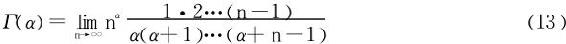
证明 据Γ函数的变形式(3):
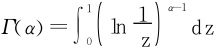
注意到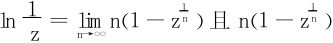 单调递增,于是极限和积分可以换序:
单调递增,于是极限和积分可以换序:
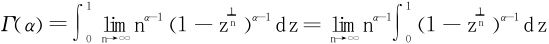
令z=yn,最终得到
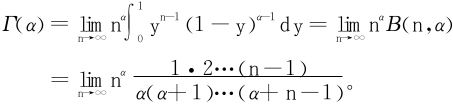
六、广义积分的计算
下面我们通过一些精选的例题讲解广义积分的非常规计算方法。不求全面,力求富有特色。
例1 计算概率积分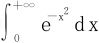 。
。
解一 利用二重积分的极坐标变换,记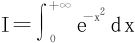 ,则
,则
解二 利用含参量积分的换序,
从而
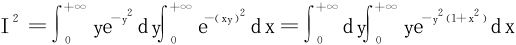
依§8.3定理3知上述积分可以换序,于是
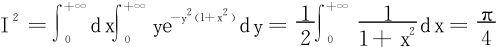
解三 利用迫敛性及Wallis公式。
因为t≠0时有et>1+t,
进而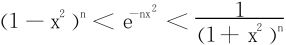 ,将此式积分有
,将此式积分有
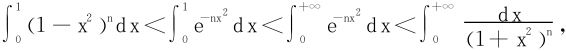
上式左端令x=sinθ,右端令x=tanθ,积分都可以化为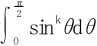 的形式,而
的形式,而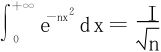 ,得到
,得到
两边平方:
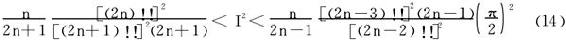
应用Wallis公式
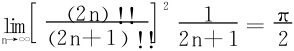
解四 利用一致收敛函数序列的性质。基于
令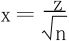 ,得
,得
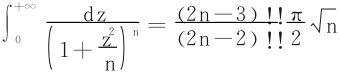
例2 计算积分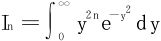 。
。
解一 分部积分法

解二 引入含参数积分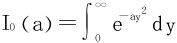 (a>0)
(a>0)
利用上述积分在a>0的内闭一致收敛性,得出可导性:
故 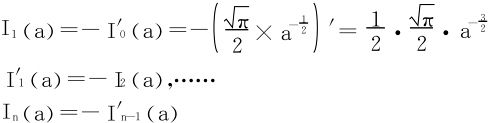
最后,令a=1,还原为非含参数积分。
解三 令y2=x,原积分可以还原为Γ函数
例3 求下列积分:

配方法: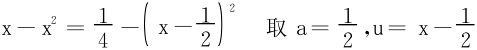
方法二 化为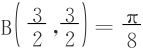
(2)方法一 令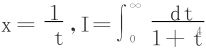
所以 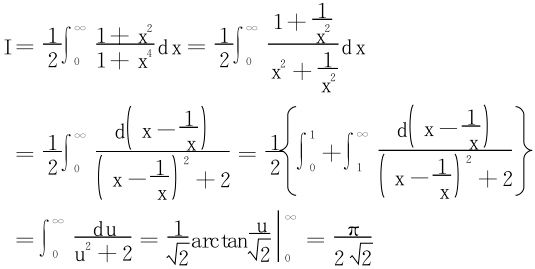
方法二 令x4=t
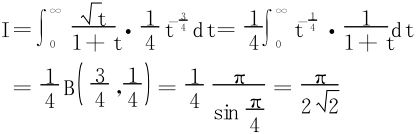
或直接将区间(0,∞)上的积分,通过变换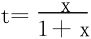 化为区间(0,1)上的积分
化为区间(0,1)上的积分
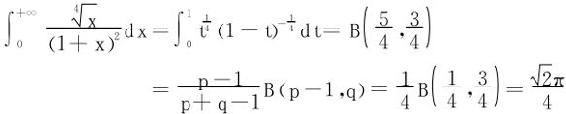
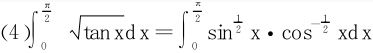
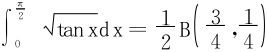
或令sin2x=t,即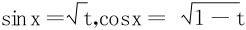 ,
,
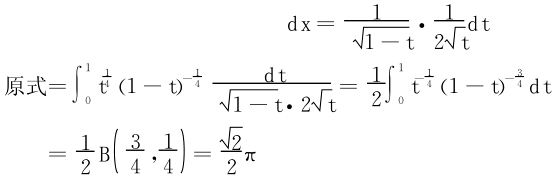
例4 利用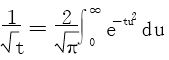 计算Fresnel积分:
计算Fresnel积分: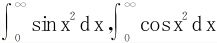 。
。
解 令x2=t,
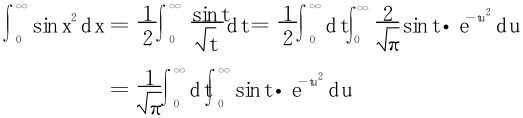
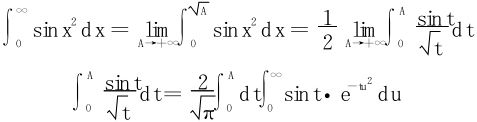
(因为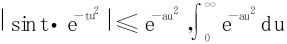 收敛)但在t=0端点处,sint因子是至关重要的。
收敛)但在t=0端点处,sint因子是至关重要的。
注 对于积分求值而言,sint因子在积分号的里面还是外面,效果是一样的,但对于一致收敛性而言,sint因子在积分号的里面还是外面,其作用截然不同。
从一致收敛的定义出发,∀ε>0找M>0,st∀G>M,∀0≤t≤A有

分析 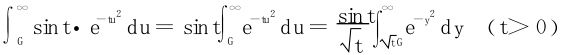
分段技术:
当0≤t≤ε2时,∀G>0
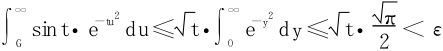
当ε2≤t≤A时,
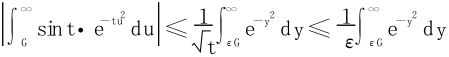
因为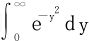 收敛,∃N>0,st∀B≥N有
收敛,∃N>0,st∀B≥N有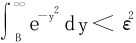 ,
,
于是(15)式成立。
对于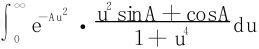
因为 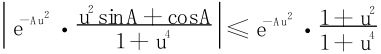
当0≤u≤1时,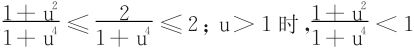
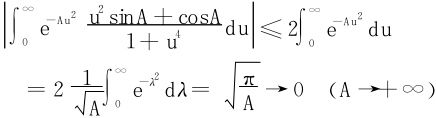
在(16)式中令A→+∞,得
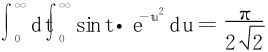
所求的Fresnel积分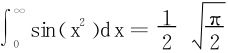
解二 引入一个“收敛因子”e-kt,令
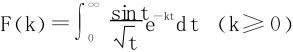
由Abel判别法,知上述无穷积分在k≥0上一致收敛。补充被积函数在t=0时的值为0,则被积函数在t≥0,k≥0上连续。于是F(k)在k≥0上连续。
下证当k>0时以下换序式成立:
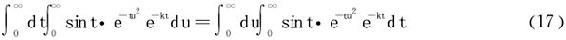
因为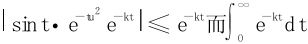 收敛。
收敛。
又依解法一,类似得
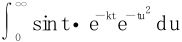 在t≥0上一致收敛(定义出发)。再考虑
在t≥0上一致收敛(定义出发)。再考虑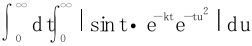 的收敛性。
的收敛性。
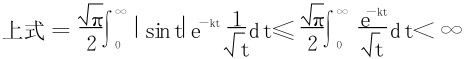
从而相关积分绝对收敛,故换序式(17)得以成立。
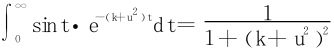
(17)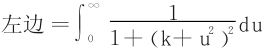
所以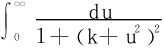 在k≥0上一致收敛。
在k≥0上一致收敛。
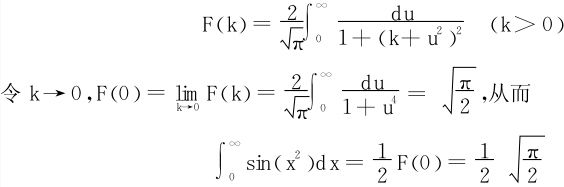
下面考虑另一个著名的积分———拉普拉斯积分。
例5 求积分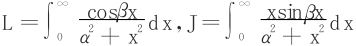 (α,β>0)。
(α,β>0)。
解一 利用公式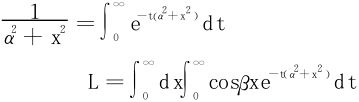
该积分能否换序呢?
思考 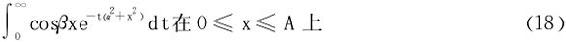
的一致收敛性。
因为 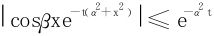

所以 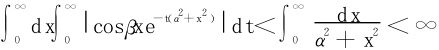
依§8.3的定理11,换序的条件并不具备。但在参考文献[6]的522段,却进行了强制的换序:
计算的结果是正确的,但过程的严密性笔者认为值得商榷。
对于另一个积分J,在求导运算和积分运算可以交换时,有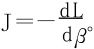 。欲可交换,考虑J关于参数β的一致收敛性。基于J(β)∀β>0都不绝对收敛(理由见下),故Weierstrass法不适用。
。欲可交换,考虑J关于参数β的一致收敛性。基于J(β)∀β>0都不绝对收敛(理由见下),故Weierstrass法不适用。
 收敛,从而J(β)不绝对收敛。
收敛,从而J(β)不绝对收敛。
现用Dirichlet判别法
当x→∞时,g(x,β)单调一致趋于0,而∀A>0,
在β>0上,并非一致有界。但在β≥β0>0上,则是一致有界。所以J(β)在β>0上内闭一致收敛。
(请读者思考J(β)在(0,+∞)上是否不一致收敛?)
从而∀β>0,有
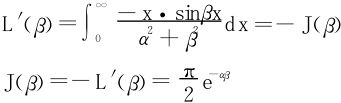
若积分可以换序(先换了再说),
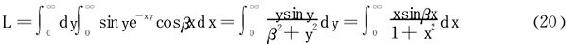
那(20)式的换序能否成立呢?
通过内闭一致收敛和有限区间上积分来转化:任取0<a<A
详见[6](第二卷524段)。
解三 从解法一已知,L′(β)=-J,往下不能求二阶导数,注意到
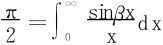
于是
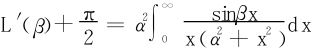
在这个积分号之下再关于β求导,则仍可以换序,
此为关于L(β)的二阶常系数线性微分方程。通解为
L(β)=C1eαβ+C2e-αβ
但
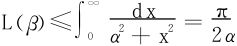 得C1=0
得C1=0
例6 设a,b>0,计算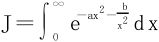 。
。
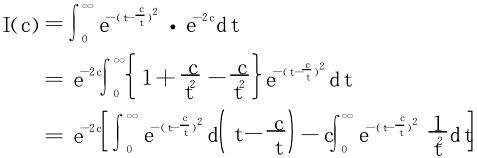
对于
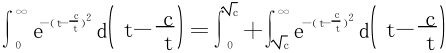
在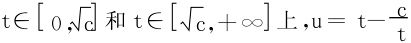 为单值对应,
为单值对应,
可得
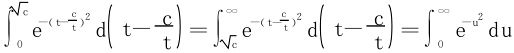
故
对于
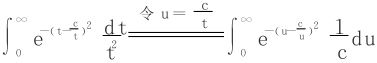
于是
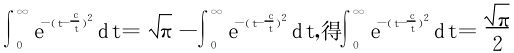
所以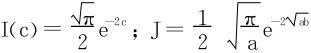
解二 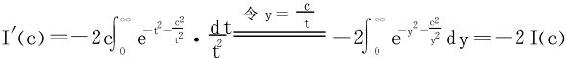
于是
显而易见,解法二要比解法一简洁得多。这也提醒我们,面对一个问题(不论是数学的或非数学的)时,发散思维、优化解法是多么重要!
七、付茹兰尼(G·Froullani)公式
在积分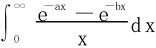 的计算中,可以利用
的计算中,可以利用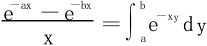 化为累次积分,然后换序。
化为累次积分,然后换序。
一般地形如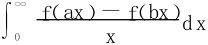 的积分如何求呢?
的积分如何求呢?
若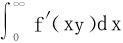 在a≤y≤b上一致收敛。则有
在a≤y≤b上一致收敛。则有
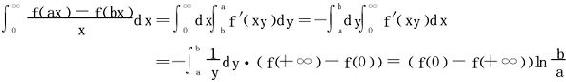
但当f仅仅连续时,又将如何?此时有如下的G.Froullani公式。
定理5 设f在[0,+∞)内连续,a>0,b>0。考虑积分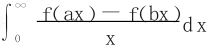
有如下的结果:
(1)若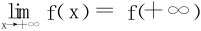 存在,则
存在,则
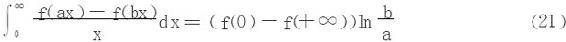
(2)若∀A>0,积分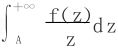 存在,则
存在,则
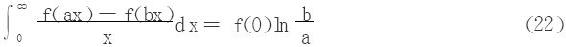
(3)若∀A>0,积分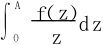 与极限f(+∞)都存在,则
与极限f(+∞)都存在,则
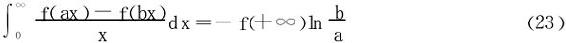
证明 ∀0<r<R<+∞
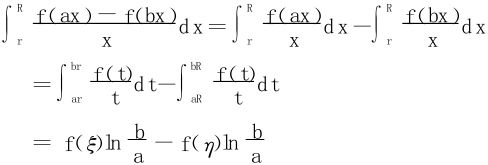
其中ξ∈(ar,br),η∈(aR,bR)
当r→0+,R→+∞时,得(21);
又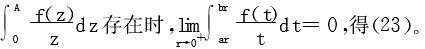 证毕
证毕
注 G. Froullani公式有三种不同的条件、结果,较难记住。理解其证明的思想将有助于我们去记忆和使用。
下面我们通过例题说明G.Froullani公式的应用。
例7 求下列积分(a>0,b>0):
解 (1)法一 利用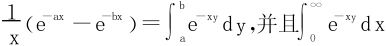 在a≤y≤b上一致收敛,从而
在a≤y≤b上一致收敛,从而
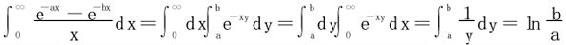
法二 利用G.Froullani公式,取f(u)=e-u,f(0)=1,f(+∞)=0,立得同样结论。
(2)取f(u)=ln(p+qe-u),f(0)=ln(p+q),f(+∞)=lnp,利用G.Froullani公式立得所求积分值是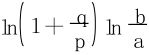 。
。
有时并不能直接用G.Froullani公式,而要对积分式加以改造才行。请看下列。
例8 求积分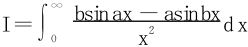 (a>0,b>0)
(a>0,b>0)
解 分部积分法
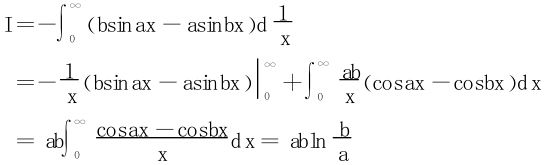
为了体现广义积分计算方法的灵活多变,我们最后再看两个例子。
例9 设a>0,b>0,求下列两个积分:
分析 此题从形式上看和例7的第(1)小题很相像,解法上当然也有一些可借鉴之处。
解 (1)法一 化为二次积分
因为 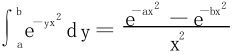 ;
;
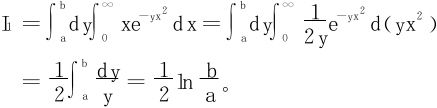
法二 凑微分法
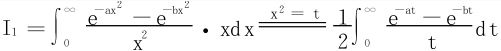
以下即例7之(1),再用G.Froullani公式就方便了。
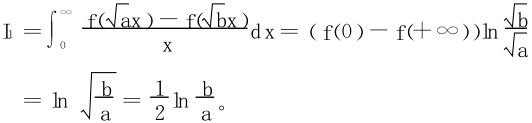
(2)法一 直接利用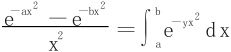
法二 利用分部积分法
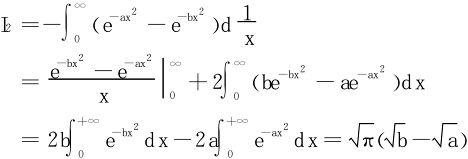
(上述两种解法都使用了概率积分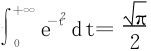 )
)
法三 利用积分号下求导,视b为参变量,改记为t:
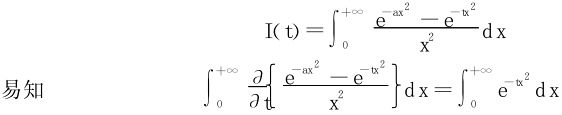
在t≥a>0上一致收敛,从而
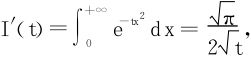
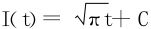 ,又
,又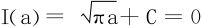 ,故
,故 ,从而
,从而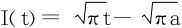 ,所以所求积分为
,所以所求积分为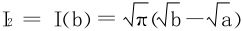 。
。
例10 计算积分
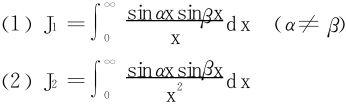
解 (1)利用三角函数的积化和差公式
直接利用G. Froullani公式得
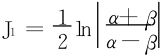
(2)采用分部积分法及积化和差
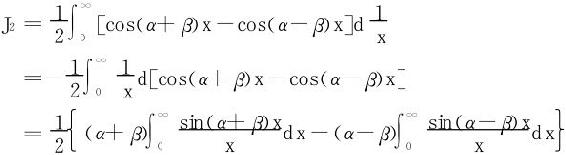
利用Dirichlet积分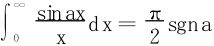 得
得
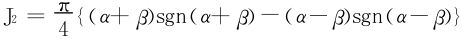
特别当0<α≤β时,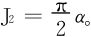 。此时积分值居然和β无关,个中缘由值得我们深思。
。此时积分值居然和β无关,个中缘由值得我们深思。
对于广义积分计算方法大的方向性的套路我们就介绍到此。有时广义积分的计算非常灵巧,一题多解更是屡见不鲜。读者朋友欲熟练地掌握这些方法,除了平时要多模仿,多练习之外,更需要从数学思维的层次上多去领悟,逐渐将其演变为自身的数学素养。
习题8.4
1.求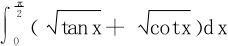 。
。
2.设a>0,b>0,求积分:
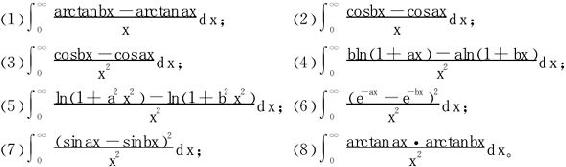
3.利用 (∑>0,n为自然数)。
(∑>0,n为自然数)。
4.利用已知积分求下列积分:
5.设α0,α1,α2,…,αn皆为正数,且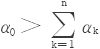 。则
。则
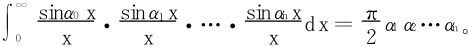
6.证明:
最后,笔者谨借老子枟道德经枠的第六十三章作为本书的结束,希望以此和各位读者共勉:
为无为,事无事,味无味。
大小多少。报怨以德。
图难于其易,为大于其细;
天下难事,必作于易;
天下大事,必作于细。
是以圣人终不为大,故能成其大。
夫轻诺必寡信,多易必多难。
是以圣人犹难之,故终无难矣。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















