极值与条件极值

§6.5　极值与条件极值

函数的极值和条件极值是函数性态的一个重要方面。在实际应用中更是占有重要的地位。在本节中，我们首先对函数极值的判定作一些回顾性叙述，然后重点讲解条件极值和拉格朗日乘数法。

一、一元函数极值

为了方便，恒设函数f在x₀的某领域U（x₀；δ）内一阶可导，在x＝x₀处二阶可导。

1．极值必要条件

定理1　（费马）函数在x₀处取得极值的必要条件是f′（x₀）＝0。

或说成：在可导的假设之下，极值点必是稳定点。

2．极值充分条件

定理2　若f′（x₀）＝0，f″（x₀）≠0，则x₀为f的极值点。具体地，

　　当f″（x₀）>0时，f在x₀处取得极小值；

　　当f″（x₀）<0时，f在x₀处取得极大值。

为了推广和形式统一的需要，我们将上述极值第二充分条件的关键语句f″（x₀）>0或f″（x₀）<0用二阶微分的形式表示之。

定理2′　设x₀为f的稳定点，则

　　当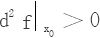时，x₀为f的极小值点；

　　当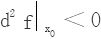时，x₀为f的极大值点。

事实上，d²f＝f″（x）dx，故二阶导数和二阶微分同号。

二、二元函数极值

设二元函数f（x，y）在P₀（x₀，y₀）的某领域内有二阶连续偏导数。

1．极值必要条件

定理3　f（x，y）在P₀（x₀，y₀）处取得极值的必要条件是：

f′_x（P₀）＝f′_y（P₀）＝0。

满足上式的P₀仍称为f的稳定点。

和一元函数相同的是：在可偏导的前提下，极值点一定是稳定点。

这样，极值点的搜索范围将大为缩小。

2．极值充分条件

定理4　设f（x，y）在P₀的邻域内有二阶连续偏导数，且P₀为f的稳定点，引入A＝f″_xx（P₀），B＝f″_xy（P₀），C＝f″_yy（P₀），Δ^*＝AC－B²，则

Δ^*<0时，P₀不是极值点；

Δ^*>0时，P₀是极值点：当A>0时为极小，A<0时为极大。

注　该定理及其证明在§3.6中有介绍。

下面我们将二元函数极值的充分条件用二阶微分的形式来表达，并设法寻求其和一元函数极值充分条件相一致的表达方式。

在§6.2节，已经讲过了全微分及其不变性。接下来我们介绍高阶微分。

三、高阶微分

设二元函数z＝f（u，v）n阶连续可偏导，其一阶微分

二阶微分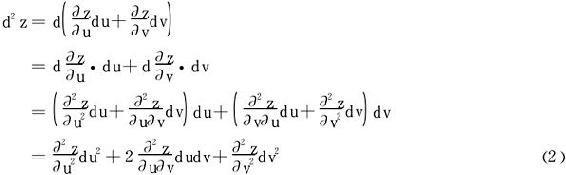

一般地，n阶微分

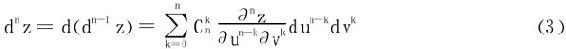
注意：上式中du^n－k＝（du）^n－k，dv^k＝（dv）^k是约定的记法。

现在问，二阶微分有没有形式不变性呢？

设u，v是中间变量，而x，y是自变量。u＝φ（x，y），v＝φ（x，y）

z＝f（u，v）＝f（φ（x，y），ψ（x，y））是（x，y）的函数。

由一阶微分的形式不变性

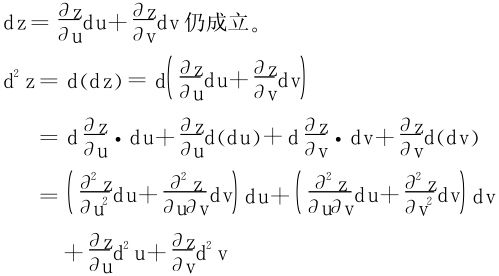
即

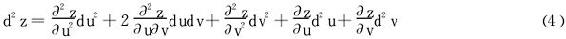
将（4）式和（2）式作一个比较，就发现u、v作为中间变量时，z的二阶微分中多出了两项。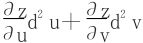

而d²u，d²v分别代表u＝φ（x，y），v＝ψ（x，y）的二阶微分，此时公式（2）仍适用。如

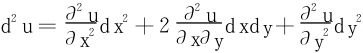
而当u，v作为自变量时，du＝Δu，dv＝Δv，d²u＝d（du）＝0，d²v＝d（dv）＝0。

所以，二阶微分不再具有形式不变性。

四、微分形式的极值充分条件

应用二阶微分的形式，我们可以将定理4改写成：

定理4′　设f（x，y）在P₀的邻域内有二阶连续偏导数，且f′_x（P₀）＝f′_y（P₀）＝0。则

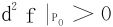　　　时，P₀必为f的极小值点；

事实上，由于dx＝Δx，dy＝Δy，f（x，y）在P₀处的二阶微分是

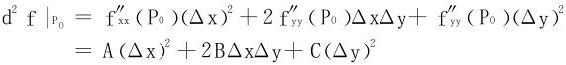
当Δ^*＝AC－B²>0时，一定保号且和A同号。

为使读者更好地理解二阶微分和极值的关系，我们以微分形式的语句给出定理4′的证明。

证明　z＝f（x，y）在P₀（x₀，y₀）处对应于Δx，Δy的全增量

Δz＝f（x₀＋Δx，y₀＋Δy）－f（x₀，y₀）；又dx＝Δx，dy＝Δy。

一阶微分dz＝f′_x（P₀）Δx＋f′_y（P₀）Δy

二阶微分d²z＝f″_xx（P₀）（Δx）²＋2f″_xy（P₀）ΔxΔy＋f″_yy（P₀）（Δy）²，

由多元Taylor公式（参见§3.6之定理1），有

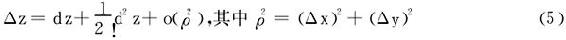
而当P₀（x₀，y₀）是f（x，y）的稳定点时，dz＝0，

于是

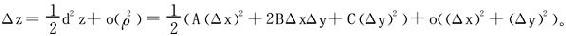
若d²z保号，则当ρ充分小时，Δz必和d²z同号。

而二次齐次式A（Δx）²＋2BΔxΔy＋C（Δy）²的判别式为

Δ＝4（B²－AC）

当Δ<0即Δ^*＝AC－B²>0时，d²z保号。

　　A>0时，d²z>0，在P₀的某领域内，Δz>0，得P₀为极小值点；

　　A<0时，d²z<0，在P₀的某领域内，Δz<0，得P₀为极大值点。

当Δ>0即Δ^*<0时，d²z变号，从而Δz在P₀的近旁也要变号，P₀不是极值点。

当Δ＝0时，存在无限多组（Δx，Δy）使得d²z＝0。

此时，Δz的符号取决于误差项o（ρ²），故无法判定P₀是否极值点。需要更高阶的微分性质才可能判定。

对一元函数来说，类似的结果可参见§3.6之例10。

比较定理2′、定理4′不难发现，在微分语句之下，一元函数和二元函数极值的充分条件就实现了形式上的统一。

五、条件极值、拉格朗日乘数法

1．条件极值问题的一般形式

在条件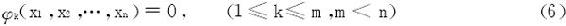　

的限制下，求目标函数z＝f（x₁，x₂，…，x_n）的极值。

为通俗易懂，我们选取n＝4，m＝2情形为代表，记号上稍作变动。

求四元函数f（x，y，u，v）在两个约束条件

之下的条件极值。

2．条件极值必要条件·拉格朗日乘数法

拉格朗日函数为

L（x，y，u，v，α，β）＝f（x，y，u，v）＋αφ（x，y，u，v）＋βψ（x，y，u，v）＝f＋αφ＋βψ

其中α，β被称作是拉格朗日乘数。

令L′_x＝L′_y＝L′_u＝L′_v＝L′_α＝L′_β＝0。

解得作为六元函数的L的稳定点M₀（x₀，y₀，u₀，v₀，α₀，β₀），而P₀（x₀，y₀，u₀，v₀）则是f（x，y，u，v）的条件极值侯选点。

简洁而稍逊严谨地讲，f（x，y，u，v）的条件极值点一定是其拉格朗日函数L（x，y，u，v，α，β）的稳定点。

仔细地加以甄别，P₀（x₀，y₀，u₀，v₀）和M0（x₀，y₀，u₀，v₀，α₀，β₀）的维度是不一样的，在条件极值的求解过程中，拉格朗日乘数α、β的确定也是非常重要的一环！

3．条件极值充分条件

在实际运用时，人们往往按第2段的方法求得了条件极值侯选点P₀后，直接依据问题的实际意义如极值一定存在，极值侯选点的唯一性等判定P₀即为所求的条件极值点。理论上的严密性比较疏忽。结合前述二阶微分和极值的关系，本段我们重点论述二阶微分和条件极值的关系，建立如下条件极值的充分条件。仍回到一般形式，拉格朗日函数为

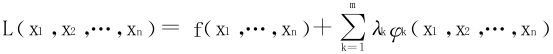
解方程组（共n＋m个方程）

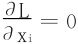（1≤i≤n），以及φ_k（x₁，x₂，…，x_n）＝0（1≤k≤m）

得出一组特定的拉格朗日乘数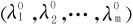，以及f的条件极值稳定点。

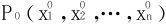现仍记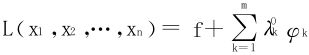　

L作为普通n元函数的二阶微分

而自变量的微分即为自变量的增量。

dx_i＝Δx_i（1≤i≤n）

但当x₁，x₂，…，x_n受到条件组φ_k（x₁，x₂，…，x_n）＝0的约束时，dx_i（1≤i≤n）之间也将受限于方程：

有了上述准备工作，我们可将条件极值的充分条件简述为：

定理5　设目标函数为f，拉格朗日函数为L，P₀为f的条件极值侯选点，则

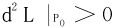　　时，P₀是f的条件极小值点；

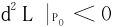　　时，P₀是f的条件极大值点。

　　d²L如（8）式所示，而dx_i（1≤i≤n）则受到方程组（9）的限制。

证明　仍以n＝4，m＝2情形为例。

设从约束条件（7）中确定了唯一的一组函数u＝u（x，y），v＝v（x，y）代入拉格朗日函数中，所得函数记为F（x，y）：

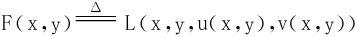
利用一阶微分的形式不变性

dF＝dL＝L_xdx＋L_ydy＋L_udu＋L_vdv

二阶微分

d²F＝d²L＝dL_x·dx＋dL_y·dy＋dL_u·du＋dL_v·dv＋L_ud²u＋L_vd²v

因为在P₀处，L_u＝L_v＝0

所以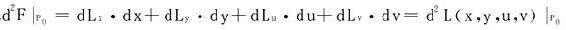

等式右端是视x，y，u，v为独立变量时，L的二阶全微分。f在约束条件（7）之下的条件极值即是F的无条件极值。依定理4′，只需判定d²F的符号。从上面推导可知，d²F即d²L，但dx，dy，du，dv必须受dφ＝dψ＝0，即

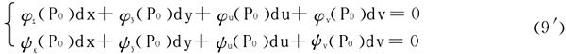
的限制。

这样，从定理4′立得定理5。

下面我们举一些条件极值及其应用（如证明不等式等）的例子。

例1　求f＝x＋y＋z＋t在限制条件xyzt＝c⁴下的极值。（x，y，z，t>0）

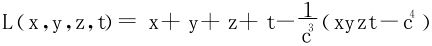
（二）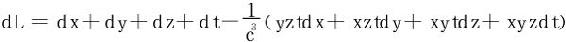　

在M₀（c，c，c，c）处，L的二阶微分

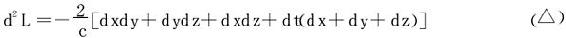
将xyzt＝c⁴两边微分：dx＋dy＋dz＋dt＝0（在M₀（c，c，c，c）处）。

亦即dz＝－（dx＋dy＋dz），代入（△）式：

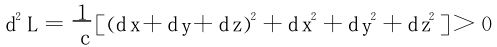
因此函数f在点（c，c，c，c）达到极小值，极小值为4c。

注　也可由几何意义判定M₀为极小值点，或代数判定无极大值，或降维考虑：x＋y在xy＝c²之下的条件极值。

证一　令。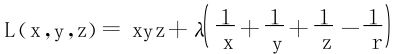

证二　令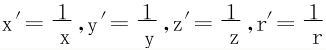原条件化为x′＋y′＋z′＝r′。

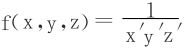　（问题的变换转化）

即在约束条件x′＋y′＋z′＝r′之下，求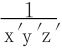的最小值。

再转化为求g（x′，y′，z′）＝x′y′z′的条件极大值。

令L（x′，y′，z′，λ）＝x′y′z′＋λ（x′＋y′＋z′－r′）。

或从约束条件解出z′＝r′－x′－y′

x′y′z′＝x′y′（r′－x′－y′），化为显函数的极值问题解得。

（或利用算术－几何平均不等式亦可）

现有不等式：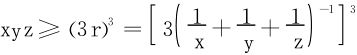

立得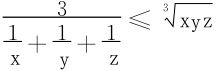　

此为调和－几何平均不等式。

现以二阶微分来验证M₀（3r，3r，3r）为极小值点。

在点M₀处

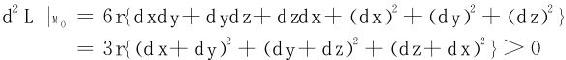
从而M₀点为条件极小值点，且是唯一的极小值点，易判定其为最小值点。

注　此处约束条件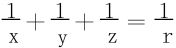的微分没有用到。

若用转换以后g（x′，y′，z′）＝x′y′z′在x′＋y′＋z′＝c之下的极值。仍记

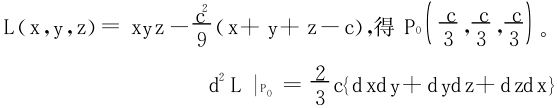
但因为x＋y＋z＝c，　所以dx＋dy＋dz＝0。dz＝－（dx＋dy）

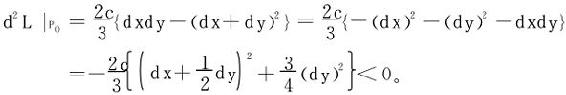
从而P₀为函数g的条件极大值点。

解一　转化为求u²＝x²＋y²＋z²的条件极值。

令L（x，y，z）＝x²＋y²＋z²＋λ［（x－y）²－z²－1］

从L′_z＝0知（λ－1）z＝0，得λ＝1或z＝0

λ＝1舍去（方程组L′_x＝L′_y＝L′_z无解）。

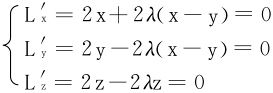
所以z＝0，代入其他式子得驻点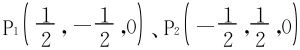，相应的乘数。

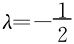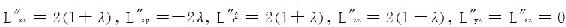
所以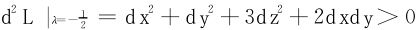

P₁，P₂为极小值点，极小值为。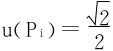

解二　以z²＝（x－y）²－1代入u²＝x²＋y²＋z²中得

v＝x²＋y²＋（x－y）²－1

令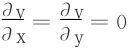解点为（0，0），但此时z无解。

于是极值应当在边界上取得。

曲面∑：（x－y）²－z²＝1定义于xy平面的区域D：｜x－y｜≥1之上。

即z²＝（x－y）²－1或写为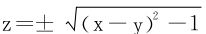

D的边界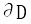：｜x－y｜＝1，代入曲面方程知z＝0。

例4　若x，y，z为满足x²＋y²＋z²＝8的正数，证明：

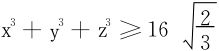
证　令F（x，y，z）＝x³＋y³＋z³

转化为求F（x，y，z）在条件x²＋y²＋z²＝8，x>0，y>0，z>0之下的条件极值。

L（x，y，z）＝F（x，y，z）＋λ（x²＋y²＋z²－8）

令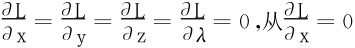即3x²＋2λx＝0知3x＋2λ＝0。

依对称性得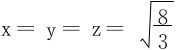，驻点为。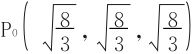

下求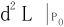

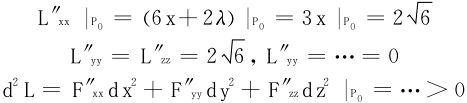
所以F（x，y，z）在P₀处取得极小值，唯一的在定义区域的内点取得的极小值必是最小值。

问：最大值在哪儿取得？答：在边界圆周上，如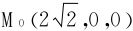处。

例5　求x>0，y>0，z>0时，函数

f（x，y，z）＝lnx＋2lny＋3lnz

在球面x²＋y²＋z²＝6r²上的极大值。并证明：a、b、c为正数时

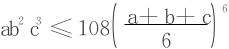
（清华大学1981年）

解　设L（x，y，z）＝lnx＋2lny＋3lnz＋λ（x²＋y²＋z²－6r²）

令L_x＝L_y＝L_y＝L_r＝0，解得。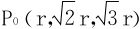

当P（x，y，z）靠近第一卦限的边界即三个坐标面时，f（x，y，z）趋于－∞。

从而唯一的稳定点P₀必是f的最大值点。

所以

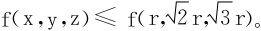
两边取指数e^{f（x，y，z）}≤e^{f（r，2r，3r）}。

得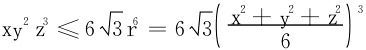　

再令x²＝a，y²＝b，z²＝c代入上式立得

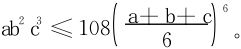
注　1．当且仅当a∶b∶c＝1∶2∶3时上述不等式中等号成立。

　　2．这种方法可用来证明许多的不等式（包括Hlder不等式），还可以自行构建出一些新的不等式。

例6　抛物面x²＋y²＝z被平面x＋y＋z＝1截得一个椭圆。求这个椭圆到原点的最长与最短距离。

解　求f＝x²＋y²＋z²在条件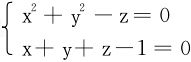之下的最值。

令L（x，y，z，λ，μ）＝x²＋y²＋z²＋λ（x²＋y²－z）＋μ（x＋y＋z－1）。

令L_x＝L_y＝L_z＝0并结合约束条件解得：

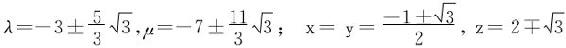
（注：注意到曲面方程关于字母的轮换对称性，在极值点处应有x＝y，或从几何意义出发分析亦可以）。

结合问题实际意义，f在有界闭集（椭圆）上必有最值。

而f的最值只能在上述两个稳定点处取得（椭圆并无端点概念，故最值点一定是稳定点）。

从而算得最大距离为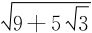，最短距离为。

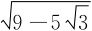又问：如何求此椭圆的长、短轴？

解一　从上面求解过程已知，椭圆长轴的两个端点是

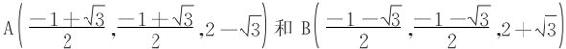
利用两点间距离公式立得长轴长为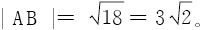

相对来说，短轴长较难求一点。

椭圆的中心在AB的中点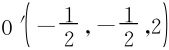处。以下求短轴所在直线方程。

长轴AB的方向数是｛x_A－x_B，y_A－y_B，z_A－z_B｝化为｛1，1，－2｝，平面x＋y＋z＝1的法向量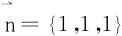。短轴CD同时垂直于A B和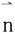，从而CD的方向数为：

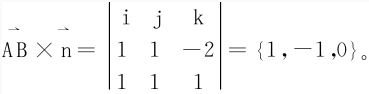
短轴CD的方程是　

联立z＝x²＋y²，解得交点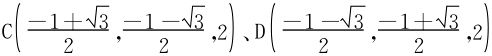

于是短轴长。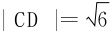

解二　先求椭圆在xy平面上的投影曲线。

解方程组

由②，z＝1－x－y，代入①：x²＋y²＝1－x－y

整理为圆方程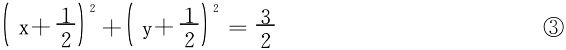

此圆的半径为。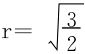

记平面x＋y＋z＝1和xy面的交角为θ。

利用几何图形或利用法向量的内积，易得

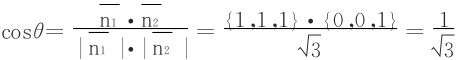
所以，长轴长。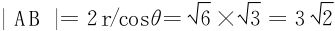

短轴CD平行于xy坐标面，故其投影即为圆③的直径，从而。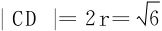

习题6.5

1．求椭圆5x²＋4xy＋2y²＝1的长半轴、短半轴长。

2．试求平面αx＋βy＋γz＝0与圆柱面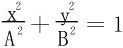相交所成椭圆的面积。

3．求函数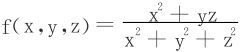在D：1≤x²＋y²＋z²≤4上的最大值、最小值。

（浙江省高等数学竞赛2007年）

4．求函数f（x，y，z）＝x⁵＋y⁵＋z⁵在x²＋y²＋z²＝8，x≥0，y≥0，z≥0之下的条件极值。

5．求方程x³＋y³－3ax＝0（a>0）所确定的隐函数y（x）的极值。

6．求曲面z＝xy－1上与原点最近的点的坐标。

（中山大学1983年）

7．给定椭球面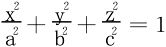，求第一卦限中椭球面的切平面，使它与坐标平面围成的四面体体积最小。

8．已知三角形的周长为2p，求出这样的三角形，当它绕着自己的一边旋转时所得旋转体的体积最大。

9．分解已知正数a为n个正的因数，使得它们的倒数的和为最小。