基于分块样本极大值法的流动性风险

7.2.1 极值理论介绍

极值理论(Extreme Value Theory，EVT)是统计学的分支，自20世纪30年代由Fisher和Tippett(1928)首次提出以来，长期应用于水力学和保险学中。极值，从统计学意义上讲，是指某一时期的随机过程的最大值和最小值，通常位于金融收益分布的尾部。EVT通过利用极限准则，研究极端样本事件对金融资产回报的“厚尾”分布建模，负责分析和解释极端事件。极值理论主要研究的是极值分布及其特征，尤其是分布的尾部特征，它是测量极端市场条件下风险损失的一种方法，具有超越样本数据的估计能力，并可以准确地描述分布尾部的分位数。

Longin(2000)提出了在股灾、金融危机等极端情形下计算Va R值的方法——极值方法。其主要思想是:计算Va R值时分别考虑两种情形，即总的市场状况以及分解成风险因子的市场状况，分别用对称稳定分布和对称多变分布进行拟合，将证券的历史收益加以分析，弥补了一般计算Va R值低估损失的缺陷。Ho等(2000)应用极值理论的方法研究了1998年亚洲金融危机中的六个亚洲国家和地区的股票市场收益率情况，发现极值方法预测的市场风险与实际情况更加接近，优于传统的Va R计算方法。然而Lee Saltogˇlu(2002)把极值理论应用于日本股票市场的风险测量，得出不同的结论，即极值方法与传统Va R计算方法在预测风险方面的结果没有大的差别。

7.2.2 基于EVT-BMM的Va R测度方法

1)次序统计量

假定X1，X2，…，Xn是取自分布函数F(x)的总体的一系列样本，将其按照升序排列，可得:X(1)≤X(2)≤…≤X(n)称(X(1)，X(2)，…，X(n))为次序统计量， X(i)为第i个次序统计量。称X(1)=min(X1，X2，…，Xn)为样本极小值， X(n)=max(X1，X2，…，Xn)为样本极大值，统称为样本极值。设F(x)为总体的分布函数，F1(x)为极小值分布函数，Fn(x)为极大值分布函数，则总体分布与他们之间有如下关系:

F1(x)=P(X(1)≤x)=1-P(X1＞x，X2＞x，…，Xn＞x)=1-(1-F(x))n　(710)

Fn(x)=P(X(n)≤x)=P(X1≤x，X2≤x，…，Xn≤x)=Fn(x)　(711)

以上两式说明，可以从总体分布得到极值分布，然而当总体分布未知的情况下，人们常用的是n→∞时所得到的极值渐进分布。

2)广义极值分布(GEV)

显然0≤F(x)≤1，当n→∞时，样本的极大值分布或极小值分布为0或1退化分布。假定存在实数列an，6n使得标准化的最大值序列Zn=(X(n)-6n)/an是依分布收敛的，其中an＞0。

定理1 (Fisher-Tippett)如果存在实数列an＞0，6n满足，当n→∞时， P{(X(n)-6n)/an≤x}=Fn(anx+6n)有非退化极限分布，则存在位置参数和尺度参数μn，σn＞0，使得当n→∞时，(712)Fn(x)-Hξ((x-μn)/σn)→0

其中，

其中参数ξ是形状参数，它决定了标准极值分布Hξ的尾部行为，当ξ＞0时，α=1/ξ称为尾部指数。如果F的尾部以指数形式衰减，Hξ是Gumbel型的，且ξ=0，Gumbel型吸引场中分布都是瘦尾的，例如，正态、对数正态、指数和伽马分布。如果F的尾部以幂函数衰减，即1-F(x)=x-1/ξL(x)，则Hξ是Frechet型的且形状参数ξ＞0。Frechet型吸引场中分布都是厚尾的，包括帕累托、柯西、t-分布。若F的尾部是有限的，则Hξ是Weibull型的且形状参数ξ＜0，Weibull型吸引场中分布有界的支集，例如，均匀分布和贝塔分布。

具体而言:

ξ＞0对应于Frechet分布，其形状参数α=1/ξ，

ξ＜0对应于Weibull分布，其形状参数α=-1/ξ

ξ=0对应于Gumbel分布，Λ(x)=exp(exp(-x))x∈R

当存在位置参数μ和尺度参数σ时，极值分布为:

3)分块样本极大值法(Block Maxima Method，BMM)

分块样本极大值法(BMM)是对大量同分布的样本分块后的极大值进行建模，将Xt的所有样本数据分成m块，每块包含n个数据，实际研究中可以按照年或季度分块。假设Xt的分布函数为F(x)，n个随机变量X1，X2，…，Xn的极大值为Mn，即Mn=max(X1，X2，…，Xn)，其分布函数为:

FMn(x)=P(Mn≤x)=P(X1≤x，X2≤x，…，Xn≤x)=Fn(x)　(717)

Fisher-Tippet定理证明存在实数列μn，σn使得正规化的最大值序列Zn=(Mn-μn)/σn是依分布收敛的，其中σn＞0。即对某个非退化的分布函数H (x)，当n→∞时有:

其中Hξ，μ，σ(x)为广义极值分布。要想得到广义极值的分布函数，需要对参数ξ，μ，σ进行估计，估计过程如下:

将总体样本数为T的样本分为m组，每组个样本个数n=T/m，令M(j)n 表示第j组内的最大值，得到序列{M(1)n，…，M(m)n }并用此来估计广义极值分布的参数。假设ξ≠0，其对数极大似然函数为:

当ξ=0时，对数极大似然函数为:

当ξ≠0时，GEV的密度函数为:

其对数似然函数为:

令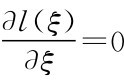，求解可得到ξ的最大似然估计。

由广义极值分布(GEV)公式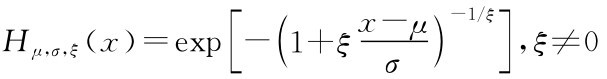，时计算分位数函数即求这个函数的反函数，并把Va R=F-1(p)代入可得:

其中，p为置信水平，n为组内样本个数，若按季节划分，则n=60。

4)基于EVT-BMM的动态Va R模型计算步骤

(1)得到流动性变化序列DLt的负数。

(2)用EVTVBMM方法估计-DLt的尾部分布，得到参数的估计值ξ和μ， β的估计值，得到最大值序列的分布函数Hξ，μ，β(x)。

(3)根据式(7-23)可以计算置信水平为q的分位数Va R(x)q。

7.2.3 基于EVT-BMM的流动性风险Va R与有效性检验[1]

1)基于分块样本极大值法的参数估计

本节所使用的数据与7.1节数据相同，详情参看7.1节。按照季度分组时，每组约60个数据，共26个块，在S-plus中用EVT-BMM方法估计-DLt的尾部分布，估计过程采用如上所述的最大似然法，参数ξ和μ，σ的估计值及其标准差和t-统计量的结果如表7-10所示。

表7-10 基于BMM的广义极值分布参数估计

表7-10的估计结果表明，上证指数和浦发银行不能拒绝参数ξ=0的原假设，说明它们处于Gumbel型的吸引场中，其流动性变化率的分布瘦尾的，例如，正态、对数正态、指数和伽马分布。而中金岭南的形状参数ξ显著大于0，则说明它处于Frechet型的吸引场中。其流动性变化率的分布是厚尾的，例如帕累托、柯西、t-分布。

2)基于EVT-BMM的Va R值及其失败率检验

根据表7-10的参数估计值，我们利用Va R(x)q=μ-σ·{1-[-ln(p)]-ξ}/ξ计算不同的置信水平下，各个样本的Va R值，这里我们分别考察了置信水平为90%，95%和99%三种情况。我们需要对得到的Va R值进行失败率检验，从而判断得到的结果是否合理。由二项式过程可得在T个样本中发生N次失败的频率为:(1-p)T-Np NKupiec提出了对零假设p=p*最适合的检验，即似然比率检验，也称为LR检验，表示为:

LR=-2ln[(1-p*)T-Np*N]+2ln[(1-N/T)T-N(N/T)N](724)

在零假设下，统计量LR服从自由度为1的χ2分布，它的95%置信水区临界值为3.84，如果LR＞3.84，则拒绝原模型。下面给出在90%、95%和99%置信水平下，采用EVT-BMM方法计算的各个样本的Va R值及采用Kupiec失败率检验法所得到的结果，如表7-11所示。

表7-11 研究样本的流动性风险Va R值及失败率检验

在模型假设合理的情况下，失败率检验的结果应该与显著性水平相接近，例如在置信水平为90%的情况下，合理的失败率应该是10%左右。表7-11中对于Va R值的失败率检验结果表明，无论是90%，95%还是99%的置信水平下，所得到的失败率次数都很低，这说明Va R值都比较保守，太保守的Va R值并不利于投资者对资产流动性风险的管理或控制。我们对比第一节采用条件方差方法动态测度流动性风险Va R值的结果，可以发现，采用EVT-BMM方法得到的Va R值均接近于动态Va R方法中计算的最大Va R值，采用极值理论计算样本Va R的方法太保守。

[1] 这部分内容摘自国家自然科学基金项目“证券市场流动性价值理论与实证分析技术”(编号:70773075)的研究成果。