宏观水平分析

(一)缺失数据填补

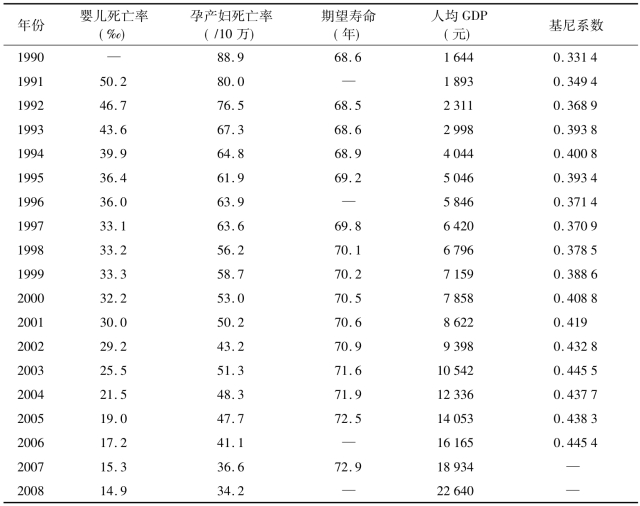
表3-1　给出了1990～2008年间全国婴儿死亡率、孕产妇死亡率、期望寿命、人均国内生产总值和基尼系数的列表。需要进行填补的数据包括1990年的婴儿死亡率，1991、1996、2006和2008年的期望寿命，以及2006～2008年的基尼系数。

表3-1　1990～2008年全国婴儿死亡率、孕产妇死亡率、期望寿命、人均GDP和基尼系数

1.基尼系数缺失数据填补

表3-1　给出了1990～2006年的基尼系数，但缺2007和2008年的基尼系数，以下采用ARIMA方法进行预测。

根据ARIMA模型的要求，基尼系数时间序列需为平稳序列，故采用ADF方法进行单位根检验。基于如下模型:

其中，Δyt代表基尼系数的一阶差分，α是常数，β是时间序列的趋势系数，p是自回归过程的滞后阶数。研究进行了不同的模型尝试，包括考虑有无漂移(常数项为0表示无漂移)以及趋势系数是否为0的情况。ADF检验的零假设为γ=0，备择假设为γ＜0。

表3-2　给出了最后的模型结果，ADF统计量(－3.64)低于5%临界值(1%临界值为－4.380，5%临界值为－3.600，10%临界值为－3.240)，故P＜0.05，拒绝γ=0的零假设，说明基尼系数时间序列不存在单位根，是平稳的时间序列。

表3-2　基尼系数时间序列平稳性的单位根检验

进一步应用ARIMA模型对2007和2008年的基尼系数进行预测。ARIMA模型预测的关键是确定参数p(自回归项数)、d(差分阶数)、q(移动平均项数)。由于基尼系数时间序列是平稳序列，故d=0。为了确定q的大小，需要考察自相关函数(autocorrelation function，ACF)。图3-1给出了基尼系数时间序列自相关图，提示移动平均项数q=1。为确定p的大小，则需考察偏自相关函数(partial autocorrelation function，PACF)。图3-2为相应的偏自相关图，提示在滞后数1处超出95%可信区间，并且在滞后数2和滞后数5处有尖钉(spike)，考虑到样本量的限制，故不纳入AR(5)过程。而且滞后数2处的尖钉超出95%可信区间不多，故似乎AR(1)过程更加适宜。综合ACF图和PACF图，ARIMA模型的选择可以有ARIMA(1，0，1)以及ARIMA(2，0，1)。

图3-1　基尼系数时间序列自相关图

注:图内阴影部分为基于Bartlett公式的MA(q)95%可信区间。

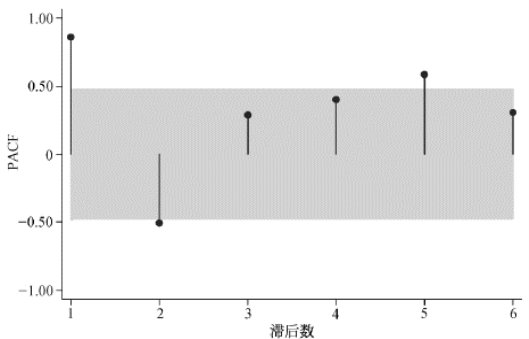
图3-2　基尼系数时间序列偏自相关图
注:图内阴影部分为95%可信区间。

ARIMA(2，0，1)模型的Wald卡方值=107.31，模型具有显著的统计学意义(P＜0.01)；ARIMA(1，0，1)模型的Wald卡方值=49.84，模型亦具有显著的统计学意义(P＜0.05)。为了进一步比较两个模型的优劣，引入Akaike信息准则(Akaike's information criterion，AIC)和Schwartz信息准则(Schwartz's bayesian criterion，SBC)来选择相较优模型。如表3-3所示，最小信息量检验显示无论是AIC准则还是SBC准则，ARIMA(1，0，1)模型的AIC函数和SBC函数都是最小的，所以ARIMA(1，0，1)是较优模型。

表3-3　应用AIC和SBC准则对ARIMA模型的比较

因此，最后根据ARIMA(1，0，1)模型对基尼系数时间序列进行预测，得到2007和2008年全国基尼系数分别为0.444 3和0.440 7。

2.期望寿命缺失数据填补

期望寿命时间序列资料中缺失1991、1996、2006和2008年的数据，以下通过3次样条函数的方法对1991、1996和2006年期望寿命数据进行插值，然后依据1990～2007年的时间序列数据应用ARIMA方法对2008年期望寿命进行预测。

应用3次样条函数插值法获得1991、1996和2006年的期望寿命数据分别为68.524 6、69.483 6、72.834 9。

基于ARIMA方法预测2008年期望寿命，与基尼系数的预测类似，也需先考察期望寿命时间序列的稳定性。研究中尝试了纳入(不纳入)常数项、纳入(不纳入)趋势项以及纳入(不纳入)一阶差分的滞后项的ADF检验，结果表明期望寿命原值(original value)是非平稳序列。因此，需要对原值序列进行变换。首先考察的是对期望寿命进行对数(自然对数)变换，类似地尝试了纳入(不纳入)常数项、纳入(不纳入)趋势项以及纳入(不纳入)一阶差分的滞后项的ADF检验，结果表明对数变换后的期望寿命时间序列是非平稳序列。其次考察对期望寿命进行一阶差分后的情况，ADF检验表明仍是非平稳序列。最后考察对数期望寿命的一阶差分序列的情况，表3-4给出了模型结果。ADF统计量(－3.018)低于5%临界值(1%临界值为－3.750，5%临界值为－3.000，10%临界值为－2.630)，故P＜0.05，拒绝零假设，说明对数期望寿命的一阶差分序列不存在单位根，是平稳的时间序列。

表3-4　对数期望寿命的一阶差分序列平稳性的单位根检验

以下应用ARIMA模型对2008年的期望寿命进行预测。首先，表3-4结果说明对数期望寿命一阶差分序列为平稳序列，故ARIMA模型中参数d=1，在实际应用中所基于的时间序列则是对数期望寿命一阶差分序列，然后再相应纳入自回归过程(AR)和移动平均过程(MA)。进一步考察自相关函数(ACF)图以确定q，图3-3给出了对数期望寿命一阶差分时间序列的自相关图，提示移动平均项数q=0。为确定p的大小，则需考察偏自相关函数(PACF)图，图3-4为相应的偏自相关图，提示在滞后数4和滞后数5处有尖钉(spike)。综合ACF图和PACF图，ARIMA模型的选择可以有AR(4)、AR(5)、AR(4，5)等3种可能模型形式。需要注意的是这3种模型都基于对数期望寿命的一阶差分时间序列。

基于AR(4)的模型Wald卡方值=4.25，模型具有显著的统计学意义(P＜0.05)；基于AR(5)的模型检验结果提示无显著的统计学意义；而基于基于AR(4，5)的模型Wald卡方值=7.15，模型具有显著的统计学意义(P＜0.05)。因此需进一步比较AR(4)和AR(4，5)两个模型的优劣。如表3-5所示，最小信息量检验显示无论是AIC准则还是SBC准则，基于AR(4)的模型的AIC函数和SBC函数都较小，所以基于AR(4)的ARIMA模型是较优模型。因此，最后基于AR(4)的ARIMA模型，得到2008年全国期望寿命为73.154 1岁。

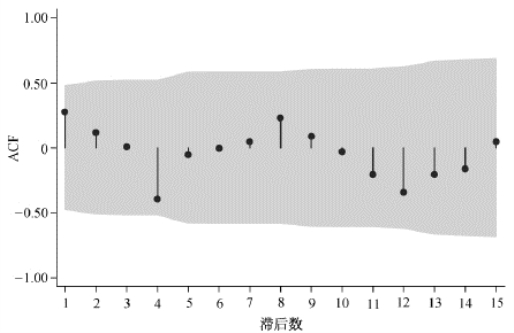
图3-3　对数期望寿命一阶差分时间序列的自相关图
注:国内阴影部分为基于Bartlett公式的MA(q)95%可信区间。

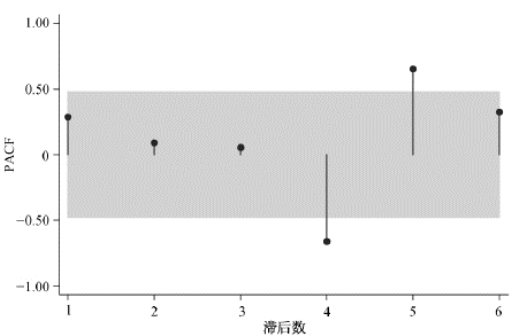
图3-4　对数期望寿命一阶差分时间序列的偏自相关图
注:国内阴影部分为95%可信区间。

表3-5　应用AIC和SBC准则对ARIMA模型的比较

3.婴儿死亡率缺失数据填补

由于1990年人口普查获得的婴儿死亡率明显低于之后附件年份的婴儿死亡率，因此从全序列数据一致性的角度考虑，将根据1991～2008年婴儿死亡率对1990年的婴儿死亡率进行估计。

1990年婴儿死亡率位于1990～2008年的婴儿死亡率时间序列的最前端，用传统意义的ARIMA模型并不能预测出1990年婴儿死亡率。因此，为了应用ARIMA模型预测1990年的婴儿死亡率，需要将实际的年份“倒过来”，从而使1990年婴儿死亡率“虚拟”地位于时间序列的最末端。具体方法是以一较大的数(如5 000)减去实际年份，然后再从小到大对新的“虚拟”年份排序，并基于该“虚拟”年份定义时间序列，按ARIMA模型的常规程序进行预测。

尝试纳入(不纳入)常数项、纳入(不纳入)趋势项以及纳入(不纳入)一阶差分的滞后项的ADF检验，结果表明“倒过来”的婴儿死亡率时间序列原值(original value)是非平稳序列。接着又尝试对原值序列进行对数(自然对数)变换，类似地尝试纳入(不纳入)常数项、纳入(不纳入)趋势项以及纳入(不纳入)一阶差分的滞后项的ADF检验，结果表明对数变换后的期望寿命时间序列还是非平稳序列。而且进一步的ADF检验结果表明，对婴儿死亡率进行一阶差分后以及将对数婴儿死亡率进行一阶差分后的序列都非平稳序列。而婴儿死亡率(原值，按“虚拟”年份序列顺序)的二阶差分序列为平稳序列，相应的ADF统计量(－5.796)低于1%临界值(1%临界值为－2.660，5%临界值为－1.950，10%临界值为－1.600)，故P＜0.01，拒绝存在单位根的零假设。

以下应用ARIMA模型进行预测。首先，婴儿死亡率二阶差分序列为平稳序列，故ARIMA模型中参数d=2，在实际应用中所基于的时间序列则是婴儿死亡率的二阶差分序列，然后再相应纳入自回归过程(AR)和移动平均过程(MA)。进一步考察自相关函数(ACF)图以确定q，图3-5给出了对数期望寿命一阶差分时间序列的自相关图，提示移动平均项数q=0。为确定p的大小，考察偏自相关函数(PACF)图，图3-6为相应的偏自相关图，提示在滞后数5处有尖钉(spike)。故综合ACF图和PACF图，ARIMA模型的选择似应为AR(5)过程，而且此时模型是基于婴儿死亡率二阶差分时间序列。

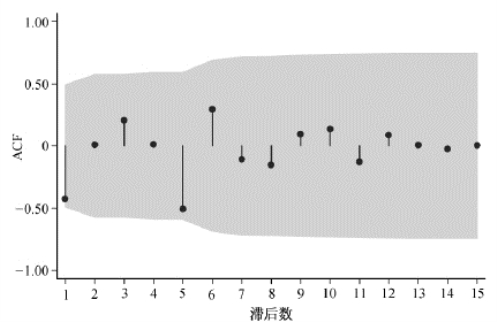
图3-5　婴儿死亡率二阶差分时间序列的自相关图
注:图内阴影部分为基于Bartlett公式的MA(q)95%可信区间。

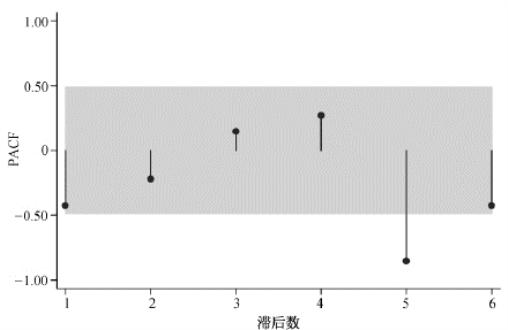
图3-6　婴儿死亡率二阶差分时间序列的偏自相关图
注:图内阴影部分为95%可信区间。

基于AR(5)的模型Wald卡方值=10.14，模型具有显著的统计学意义(P＜0.01)。因此，最后基于AR(5)的ARIMA模型，得到1990年全国婴儿死亡率为55.478 4‰。

表3-6为完成缺失数据填补后1990～2008年全国婴儿死亡率、孕产妇死亡率、期望寿命、人均GDP和基尼系数的列表，这也是接下来对各人群健康指标与基尼系数的时间序列关联进行分析的基础。

表3-6　1990～2008年全国婴儿死亡率、孕产妇死亡率、期望寿命、人均GDP和基尼系数

(二)时间序列平稳性检验

虽然前述应用ARIMA模型对人群健康指标(婴儿死亡率和期望寿命)以及基尼系数的缺失数据进行预测时，对相关时间序列的平稳性进行了检验。但对表3-6各指标1990～2008年的完整时间序列仍有必要开展平稳性检验，并以此为基础进入后续的协整分析和因果关系分析。

对时间序列平稳性的检验(单位根检验)仍然采用ADF方法。在之后的结果叙述中，以IMR代表婴儿死亡率、MMR代表孕产妇死亡率、LE代表期望寿命、PGDP代表人均国内生产总值、GINI代表基尼系数。以时间序列为原值序列，对一阶差分以Δ标记，如ΔIMR表示IMR的一阶差分。如果ADF检验提示某时间序列的原值序列为平稳的(即拒绝零假设:存在单位根)，则该时间序列为0阶单整序列，记为I(0)；如果ADF检验提示某时间序列的原值序列为非平稳序列(即不能拒绝零假设)，而其一阶差分后的时间序列为平稳序列，则该时间序列为1阶单整序列，记为I(1)，余类推。

表3-7　给出了对各指标时间序列的ADF检验结果，原值序列为单整序列的包括IMR、MMR和GINI；一阶差分序列为单整序列的包括IMR、MMR、LE和GINI；二阶差分序列为单整序列的包括IMR、MMR、LE和GINI。值得注意的是LE原值序列为非平稳时间序列，而PGDP原值、一阶差分和二阶差分序列均为非平稳序列。

表3-7　时间序列变量的单位根检验

为了便于结果的解释(主要是回归方程系数的解释，使之代表弹性)，常对变量进行自然对数变换(以Ln表示)。本研究中LnIMR表示婴儿死亡率的自然对数，如此类推。以自然对数变换后的时间序列为原值序列，对一阶差分以Δ标记，如ΔLnIMR表示LnIMR的一阶差分。

表3-8　给出了对各指标取自然对数后的时间序列ADF检验结果，原值序列为单整序列的包括LnIMR、LnMMR、LnPGDP和LnGINI；一阶差分序列为单整序列的包括LnMMR、LnLE和LnGINI；二阶差分序列为单整序列的包括LnIMR、LnMMR、LnLE、LnPGDP和LnGINI。而LnLE原值序列仍为非平稳时间序列，LnIMR一阶差分序列和LnPGDP一阶差分序列亦为非平稳序列。

表3-8　时间序列变量的单位根检验

(三)协整检验

根据表3-7和表3-8给出的时间序列单位根检验结果，以下采用Johansen (1988，1991)以及Johansen和Juselius(1990，1992)提出的协整检验方法进一考察IMR(LnIMR)、MMR(LnMMR)、LE(LnLE)等人群健康变量分别与PGDP (LnPGDP)和GINI(LnGINI)等经济变量的协整关系。协整关系意味着在两个时间序列变量之间存在长期(或均衡)的线性关系，是可以进一步利用传统回归模型进行分析的前提条件。

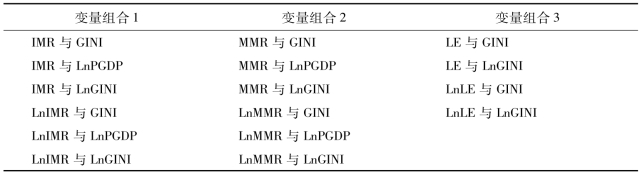
首先考察1个被解释变量与1个解释变量构成的回归模型。由于协整关系检验的基本条件是所检验的两个时间序列变量为同阶单整序列，故根据表3-7和表3-8以及尽量选择低阶为原则(便于将来结果的解释)，分别对如下变量组合进行协整检验(表3-9)。

表3-9　时间序列协整检验的变量组合

对任何变量组合采取如下方程形式进行协整检验，即

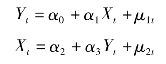
方程中的Y与X表示表3-9中列出的任一变量组合。

在Johansen过程中考察迹检验(trace test)和最大特征值检验(maximum eigenvalue test)这两个统计检验。在实际应用中，迹检验统计量和最大特征值统计量都需根据模型基于不同的滞后情况进行计算。确定滞后数的依据是上述模型获得的上述两个统计量的值最小，滞后数的确定有助于了解模型的短期动态(short-run dynamics)，也可进一步利用AIC准则和SBC准则帮助判断向量自回归(vector autoregression)滞后阶数。考虑到样本量较小，本研究根据Cheung和Lai (1993)的建议选择迹检验［90］。原因是与最大特征值检验相比，迹检验中残差的偏度和峰度都更稳健。

协整检验的零假设是协整关系的数量(the number of cointegration vectors)等于r，备择假设是有超过r个协整关系。拒绝零假设意味着迹检验统计量大于临界值。首先检验H0∶r=0，如果拒绝该零假设，再接着检验H0∶r=1。直到拒绝零假设，则停止检验。此时的r值即为关于协整关系数量的估计。实际检验中考虑了约束的线性趋势(restricted linear trend)。

表3-10　给出了协整检验的结果。除变量组合(IMR与GINI)、(IMR与LnPGDP)、(IMR与LnGINI)外，其余所有变量组合的协整检验零假设(H0∶r=0)在5%的统计意义水平未被拒绝。换句话说，检验结果表明这些变量组合内的两个变量不协整。在3个零假设(H0∶r=0)被拒绝的变量组合中，继续检验第2个零假设(H0∶r=1)，该零假设均未被拒绝，故婴儿死亡率与基尼系数、人均GDP的自然对数以及基尼系数的自然对数这3个变量存在协整。其中婴儿死亡率与基尼系数之间为(0，0)阶协整［或(1，1)阶、(2，2)阶协整］，婴儿死亡率与人均GDP的自然对数之间为(0，0)阶协整或(2，2)阶协整，婴儿死亡率与基尼系数的自然对数之间为(0，0)阶协整［或(1，1)阶、(2，2)阶协整］。表3-10还根据迹检验统计量最小化的原则确定了滞后阶数，为开展协整变量Granger因果关系检验时VAR模型中滞后阶数的确定提供了依据。

表3-10　协整检验结果

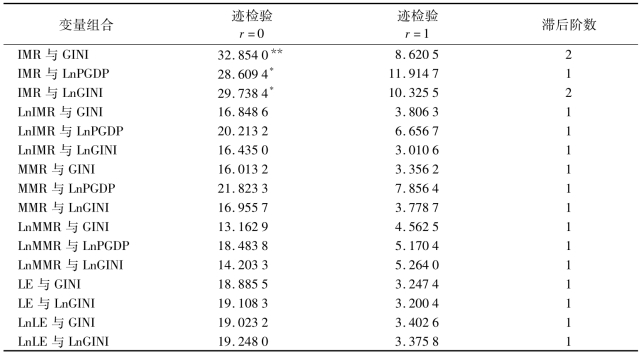
注:*表示P＜0.05；＊＊表示P＜0.01。

(四)Granger因果关系检验

Engle和Granger(1987)及Granger(1988)指出:如果两个时间序列变量协整，那么两者之间至少存在一个单向的Granger因果关系。以下针对上述3个协整变量组合进一步开展Granger因果关系检验，以确定变量组合中两个变量之间因果关系的方向。具体方法是，首先针对通过协整检验的两个时间序列变量采用向量自回归VAR模型(因两个时间序列变量是协整的，故可用变量原值)，然后进行Granger因果关系检验。

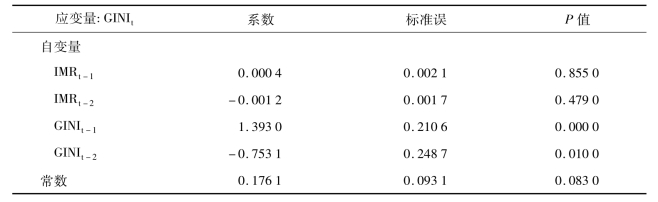
表3-11　和表3-12为针对婴儿死亡率(IMR)和基尼系数(GINI)的VAR模型结果，前一部分协整检验给出适宜滞后阶数为2。比较不同滞后阶数VAR模型的AIC和SBC结果，滞后阶数2的模型亦为最优模型。而且考虑到研究所采用的时间序列为1990～2008年的数据，属于小样本，故应用了小样本条件下自由度的调整(small sample degrees of freedom adjustment)，并相应计算小样本t统计量和F统计量。从表3-11可以看出，对IMR而言，IMR一阶滞后效应具有显著的统计学意义(P=0.009)；GINI一阶滞后项的系数虽为负，但无显著的统计学意义(P=0.079)。而表3-12则未显示IMR对GINI的滞后效应。基于VAR模型的Granger因果关系检验结果表明，IMR不是GINI的Granger原因，但GINI是IMR的Granger原因(统计量F=5.353 2，P=0.021 8)，虽然表3-11的VAR模型中GINIt-1的系数检验P＞0.05。

表3-11　IMR与GINI的VAR模型Ⅰ

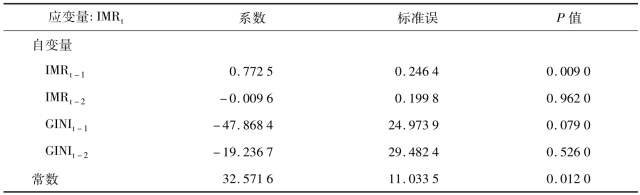
表3-12　IMR与GINI的VAR模型Ⅱ

对另两个存在协整关系的变量(IMR与LnPGDP，IMR与LnGINI)以进行类似的VAR模型过程和Granger因果关系检验。表3-13、表3-14、表3-15和表3-16分别给出了VAR模型结果，其中IMR与LnPGDP的VAR模型滞后阶数取1，IMR与LnGINI的VAR模型滞后阶数取2。而且也应用了小样本条件下自由度的调整，并相应计算小样本t统计量和F统计量。

从表3-13可以看出，对IMR而言，IMR一阶滞后效应具有显著的统计学意义(P=0.001 0)，LnPGDP一阶滞后效应无显著统计学意义(P=0.711 0)。表3-14则显示IMR对LnPGDP的一阶滞后效应具有显著的统计学意义(P=0.002)，而且系数为负。基于VAR模型的Granger因果关系检验结果表明，IMR是LnPGDP的Granger原因(统计量F=14.719，P=0.001 6)，而LnPGDP不是IMR的Granger原因。

表3-13　IMR与LnPGDP的VAR模型Ⅰ

表3-14　IMR与LnPGDP的VAR模型Ⅱ

表3-15和表3-16为针对婴儿死亡率(IMR)和基尼系数的自然对数(LnGINI)的VAR模型结果，滞后阶数为2。从表3-15可以看出，对IMR而言，IMR一阶滞后效应具有显著的统计学意义(P=0.005)，LnGINI一阶滞后效应无显著统计学意义(P=0.091 0)。表3-16显示IMR对LnGINI的滞后效应。基于VAR模型的Granger因果关系检验结果表明，IMR不是GINI的Granger原因，而LnGINI是IMR的Granger原因(统计量F=4.515 4，P=0.034 5)，虽然在表3-15的VAR模型中LnGINIt-1系数检验并无显著统计学意义。

表3-15　IMR与LnGINI的VAR模型Ⅰ

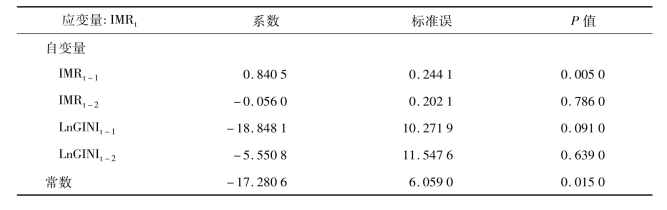
表3-16　IMR与LnGINI的VAR模型Ⅱ

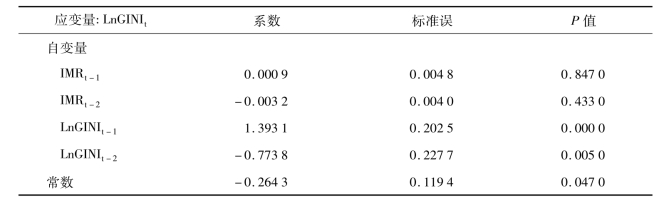
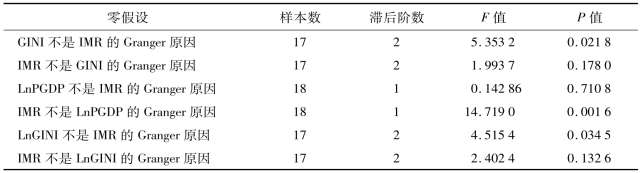
表3-17　综合了上述关于Granger因果关系检验的结果。可以看出，研究中所选择的两个经济变量(基尼系数和人均GDP)对婴儿死亡率的效应是不同的，人均GDP的自然对数(LnGDP)不是IMR的Granger原因，基尼系数(基尼系数的对数)却是IMR的Granger原因。而且值得注意的是系数为负，即上一期较高的基尼系数将使本期婴儿死亡率较低。

表3-17　G ranger因果关系检验结果

(五)误差修正模型

按照协整理论，几个同阶单整的时间序列变量之间的协整关系反映的是变量间存在一种长期的稳定关系(或均衡，equilibrium)，意味着此时仍可用变量原值进行传统回归方法分析，但这样的分析不能反映协整变量间的短期关系。误差修正模型(VEC模型)就是建立在协整理论基础之上，而且能够同时考察短期和长期效应的有效工具。

Johansen发展的VEC模型可以很方便地描述多变量之间的长期均衡关系与短期波动，揭示系统的动态属性。在VEC模型中各个差分项前的系数反应了变量短期波动的影响，而误差项(常记为CEt-1)前的系数则描述在扰动发生致使本期应变量偏离其长期均衡水平时，下一期应变量向长期均衡水平调整的方向和速度。

前述的研究结果显示婴儿死亡率(IMR)不仅与基尼系数(GINI，LnGINI)协整(cointegrated)，而且基尼系数(GINI，LnGINI)是婴儿死亡率的Granger原因。以下通过构建误差修正模型(VEC模型)探讨基尼系数对婴儿死亡率的短期和长期效应。由于VAR模型提示滞后阶数为2，故VEC模型的滞后阶数则为1。而且由于在协整过程中考虑了约束的线性趋势项，故在VEC模型中同样考虑。具体模型形式如下:

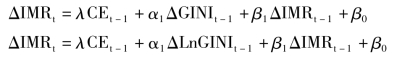
表3-18　给出了IMR与GINI的误差修正模型，CEt-1代表误差项。VEC模型结果显示，从短期来看，基尼系数对婴儿死亡率的影响不大，针对其系数的检验未显示有显著统计学意义(P=0.336 0)；而且婴儿死亡率滞后一期对其本期婴儿死亡率的效应亦无显著统计学意义。而从长期看，如果本期的婴儿死亡率偏离长期均衡，那么在下一时期这种偏离的修正很小(3.58%)，而且该修正无显著的统计学意义(P=0.100 0)。

表3-18　IMR与GINI的误差修正模型

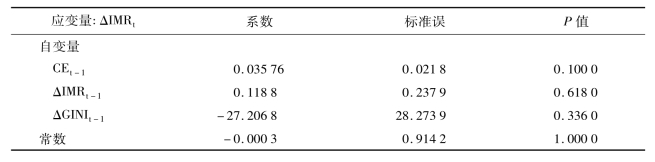
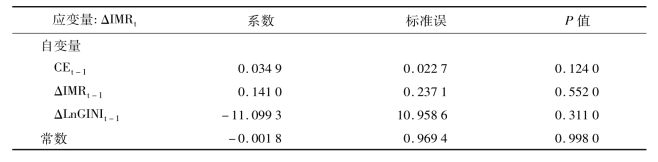
表3-19　给出了IMR与LnGINI的误差修正模型。VEC模型结果显示，从短期来看，基尼系数(自然对数变换)对婴儿死亡率的影响亦不大，针对其系数的检验未显示有显著统计学意义(P=0.124 0)；而且婴儿死亡率滞后一期对其本期婴儿死亡率的效应亦无显著统计学意义。而从长期看，如果本期的婴儿死亡率偏离长期均衡，那么在下一时期这种偏离的修正很小(3.49%)，而且该修正无显著的统计学意义(P=0.124 0)。

表3-19　IMR与LnGINI的误差修正模型

除了上述两个VEC模型之外，还可基于LnPGDP与IMR之间的协整关系以及IMR是LnPGDP的Granger原因而构建VEC模型。根据协整检验，在VAR模型给出的滞后阶数为1，在VEC模型中滞后阶数为0。在这种情况下，虽然仍能得出VEC模型结果。但该VEC模型中已经没有短期效应项，即没有ΔIMRt-1和ΔLnPGDPt-1项。虽然短期效应难以判断，但长期均衡中所依赖的Granger因果关系的方向(IMR是LnPGDP的Granger原因，而不是相反)却似乎提示有必要在多变量框架下同时纳入LnPGDP与GINI(或LnGINI)进行考察，从而避免两个时间序列变量协整关系和Granger因果关系判断中可能出现的较难解释的情况，以及给出基尼系数独立效应的判断。

事实上，与在前面的分析中，无论是协整检验还是Granger因果关系检验，考察的都是双变量之间的协整关系以及相应的Granger因果关系。现实中往往需要考察多变量之间的关系。以婴儿死亡率为例，研究中分别考察了婴儿死亡率与人均GDP和基尼系数的关系，但两者可能同时对婴儿死亡率起作用(虽然在表3-17中没有看到LnPGDP成为IMR的Granger原因)，并且大量研究收入不平等与人群健康变量之间生态关联的文献都会同时将人均GDP与基尼系数纳入模型方程。这一方面反映了人们对绝对经济水平影响人群健康的一般认识，同时也有助于在控制“绝对收入假设”的前提下考察基尼系数的独立效应(即“相对收入假设”)。此外，协整关系检验需要基于VAR模型，如果仅纳入LnPGDP，则实际上反映的是LnPGDP对IMR的线性效应。虽然本研究重点考察的是基尼系数对人群健康的独立效应，但仍然需要在控制LnPGDP的条件下进行。在绝对收入假设中，人们通常认为收入对人群健康的效应是边际递减的，因此从拟合最优模型的角度，有必要考虑在VAR模型和VEC模型中纳入LnPGDP的非线性效应，一般的做法是纳入LnPGDP的平方项(记为(LnPGDP)2)，但仍然需要考察其平稳性。ADF检验的结果表明1990～2008年的(LnPGDP)2时间序列是平稳序列，其一阶差分为非平稳序列，而二阶差分为平稳序列。为了确定纳入非线性项(LnPGDP)2的统计意义，需要比较无(LnPGDP)2和有(LnPGDP)2项的VAR模型优劣，可采用比较AIC、SBC和对数似然值(log likelihood)的方法。

表3-20　为未纳入(LnPGDP)2项的VAR模型(滞后阶数为2)。结果表明，IMRt-1和GINIt-1对IMRt的效应具有显著的统计学意义。表3-21为纳入(LnPGDP2)项的VAR模型(滞后阶数为2)，IMRt-1对IMRt的效应仍具有显著的统计学意义，但GINIt-1对IMRt的效应则无显著的统计学意义。比较对数似然值以及AIC和SBC，IMR与LnPGDP、(LnPGDP)2及GINI组成的VAR模型较优。

表3-20　IMR与LnPGDP及GINI的VAR模型

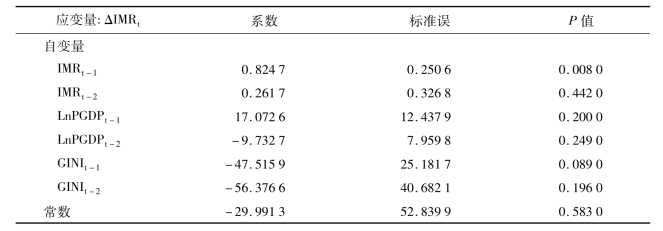
注:n=17；对数似然值=87.808 8；AIC=－7.859 9；SBC=－6.830 5。

表3-21　IMR与LnPGDP、(LnPGDP)2及GINI的VAR模型

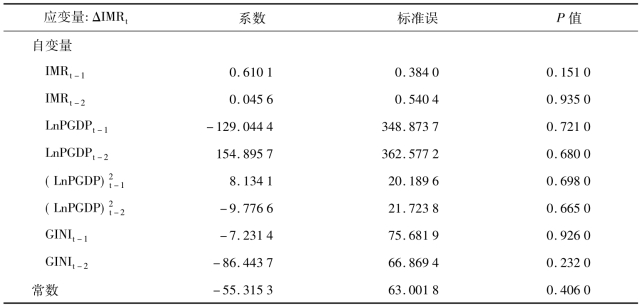
注:n=17；对数似然值=151.167 8；AIC=－13.549 2；SBC=－11.784 7。

针对表3-20和表3-21的VAR模型进行Granger因果关系检验。结果表明，在多变量框架及未纳入(LnPGDP)2的情况下，GINI是IMR的Granger原因(Granger因果关系检验F=5.570 1，P=0.023 7)；但在纳入(LnPGDP)2的情况下，GINI则不是IMR的Granger原因(Granger因果关系检验F=3.094 2，P=0.101 1)。

上述所进行的协整检验为双变量协整检验，但事实上协整检验并不排除多变量之间的协整，只是对纳入协整的被解释变量和解释变量的单整阶数的要求与双变量协整检验的要求有所区别。多变量协整检验并不要求被解释变量与解释变量(≥2个)同阶单整(因为多个解释变量的组合可能降低阶数)，但被解释变量的单整阶数需小于解释变量的单整阶数，而且不同解释变量的单整阶数则需相同。鉴于前面的VEC模型结果(表3-18和表3-19)显示，GINI和LnGINI对IMR的长期和短期效应类似，而且为了有利于说明模型系数的意义，故在以下分析中采用GINI。因此，多变量协整关系检验将在IMR、LnPGDP、(LnPGDP)2和GINI之间进行。为满足多变量协整对被解释变量和解释变量的阶数要求，以IMR为一阶单整变量，即I(1)，而LnPGDP、(LnPGDP)2和GINI均为二阶单整变量，即I(2)。

表3-22　给出了针对IMR、LnPGDP、(LnPGDP)2和GINI的多变量Johansen协整检验结果。协整检验纳入约束线性时间趋势，并尝试不同的滞后阶数，通过比较AIC和SBC的大小，判断适宜滞后阶数为2。表3-22的第1个迹检验统计量大于1%水平下的临界值(112.30＞70.05)，第2个迹检验统计量大于1%水平下的临界值(54.67＞48.45)，第3个迹检验统计量亦大于1%水平下的临界值(27.57＞25.32)，但第4个迹检验统计量低于5%水平下的临界值(11.59＜12.25)，说明有3个协整方程存在。要证明协整方程的具体形式，可通过EG两步法进行协整检验。由于包含IMR、LnPGDP和GINI的多变量协整方程可以有不同的方程形式(即被解释变量和解释变量的设定)，故首先考虑以IMR为被解释变量而LnPGDP、(LnPGDP)2和GINI为解释变量的方程形式，协整方程如下:

IMR=109.900 2－0.239 7×LnPGDP－0.779 4×(LnPGDP)2－35.790 9×GINI

其中，LnPGDP、(LnPGDP)2以及GINI的系数检验均无显著统计学意义。要进行协整检验须对上述回归模型的残差序列进行检验，若残差是平稳的，则可确定各变量之间存在协整关系。检验方法采用ADF检验。结果表明，ADF统计值为－2.761(无常数项模型形式下的检验结果)，小于1%水平的统计意义临界值(－2.660)，故在1%的显著性水平下拒绝存在单位根的原假设，即以IMR为被解释变量和以LnPGDP、(LnPGDP)2及GINI为解释变量构成的回归模型的残差序列是平稳的，亦即IMR与LnPGDP、(LnPGDP)2及GINI是协整的。

表3-22　协整检验结果

注:表中r代表协整方程个数。

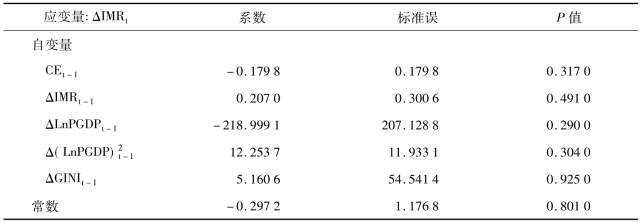
基于上述协整检验，以下进一步拟合VEC模型。表3-23结果显示，从短期来看，基尼系数对婴儿死亡率的影响亦不大，针对其系数的检验显示无显著统计学意义(P=0.925 0)；而且婴儿死亡率滞后一期对其本期婴儿死亡率的效应亦无显著统计学意义。而从长期看，如果本期的婴儿死亡率偏离长期均衡，那么在下一时期对这种偏离的修正为17.98%，但该修正无显著统计学意义(P=0.124 0)。

表3-23　IMR与LnPGDP、(LnPGDP)2及GINI的VEC模型

(六)脉冲响应分析

从上述VEC模型的结果不难看出，无论是人均GDP的自然对数(LnPGDP)还是基尼系数(GINI)，从短期看对IMR的影响都是有限的。但VEC模型所考虑的滞后阶数与VAR模型一样均为2，VAR模型和VEC模型是从时间序列数据本身的特点进行滞后阶数的选择，而且事实上由于VEC模型进行了一阶差分，故表3-23显示的滞后阶数仅为1。人们往往还关心各个解释变量［这里是LnPGDP、(LnPGDP)2和GINI］对被解释变量(IMR)的持续性(长期性)独立效应(VEC模型中误差项CEt-1的系数反映的是总体上对长期均衡的修正大小和方向)，因此需要基于更长期滞后期的考察。脉冲响应分析为此提供了有效的分析工具，通过获得脉冲响应函数(impulse response function，IRF)，描述在扰动项上加上一个标准差大小的冲击对内生变量当前值和未来值所带来的影响。对变量的冲击直接影响到该变量本身，并且通过VAR模型或VEC模型的动态结构传导给其他所有的内生变量。脉冲响应函数理论上可以无限期地推导脉冲响应函数(这与时间序列数据的长度无关)。本部分所进行的脉冲响应分析首先考察10年滞后期的脉冲响应，然后再放大到30年滞后期的情况。

脉冲响应函数的估计可以基于VAR模型也可以基于VEC模型，不同的基础模型选择会对结果的解释带来影响。事实上VAR模型与VEC模型也是有联系的，之前进行的协整检验的潜在依据就是VAR模型，VEC模型是带约束条件(即加入通过协整方程获得的误差修正项CEt-1)的VAR模型。前面分析中所基于的VAR模型考察的是解释变量原值(水平)的滞后对被解释变量原值(水平)的效应，而相应的VEC模型却是基于原值差分(增量)的角度进行考察，并且能够较好地判断出短期效应。通过VEC模型获得的长期效应主要基于对总体长期均衡偏离的修正大小和方向的判断，并不能给出某个特定解释变量的扰动对被解释变量带来的短期和长期效应，而这正是脉冲响应分析所要解决的问题。

以下给出在10年滞后期框架的脉冲响应分析，分别画出基于VAR模型和VEC模型的脉冲响应函数图。由于解释变量涉及LnPGDP、(LnPGDP)2和GINI等3个变量，故将这3个变量的脉冲响应函数叠加(overlay)在一张图内，以进行比较分析。

与前面的分析一致，基于表3-21的VAR模型计算10年滞后期的脉冲响应函数(IRF)，为了更直观地利用脉冲响应函数分析变量之间的动态响应特征，画出相应的脉冲响应函数图(图3-7)。在滞后期为10年的框架内观察LnPGDP和GINI对IMR的影响，LnGDP一个单位标准差冲击在初期就对IMR产生了负影响，到第3期达到最大后衰减，但在全部10个滞后时期内均表现为负影响。GINI变量的一个标准差冲击对IMR也具有较持续的负影响，其影响呈现了先增大(在第4期达到最大)再减小的过程。比较LnPGDP和GINI的脉冲响应，IMR对两者冲击的响应方向一致。但不难看出，除了第2期，IMR对LnPGDP冲击的响应明显高于对GINI冲击的响应，两者在最高响应区间(第3期到第5期)的响应值差2倍(LnPGDP脉冲响应值接近－300，而对应GINI的脉冲响应值仅接近－100)。而与LnPGDP和GINI不同，(LnPGDP)2的冲击所带来的IMR响应表现为持续性低水平的正影响。若在滞后期为30年的更长时间段看(图3-8)，(LnPGDP)2仍然表现为持续低水平的正影响，无论是LnPGDP还是GINI的脉冲响应都是在第3至第5期的高位负影响滞后出现持续衰减，GINI的脉冲影响大约在第20期左右达到最低，而LnPGDP的脉冲影响则约在第30期达到最低。

从图3-7和图3-8所显示的脉冲响应图的实际意义看，LnPGDP和GINI对IMR的滞后效应的方向一致，相互间加强了综合效应，而且GINI的滞后效应(负影响)明显弱于LnPGDP的滞后效应。从长期看，LnPGDP对IMR的影响(负影响，即婴儿死亡率下降)的持续性也长于GINI。因此，结合图3-7和图3-8，至少可以认为，即使存在基尼系数的独立滞后效应(负影响)，这种滞后效应也很容易被LnPGDP的更强烈的负影响所掩盖。

图3-9　和图3-10给出了基于VEC模型的脉冲响应图。如图3-9所示，首先在滞后期为10年的框架内看LnPGDP和GINI对ΔIMR的影响(严格地说，应该是ΔLnPGDP和ΔGINI对ΔIMR的影响)，ΔLnPGDP一个单位标准差冲击在初期(第1期和第2期)就表现为对ΔIMR的负影响，至第4期达到最大，脉冲响应值略高于－600，之后影响出现持续衰减，至第9期和第10期约衰减一半。ΔGINI变量的一个标准差冲击对IMR的负影响则与ΔLnPGDP不同，在全部10个滞后期，ΔGINI脉冲响应曲线的响应值均表现为正影响，在第4期达到最大，然后出现衰减。Δ(LnPGDP)2则持续表现为低水平的正影响。如图3-10所示，从滞后期为30年的更长区间段看，ΔLnPGDP效应仍然为负影响，在第10期后效应基本维持在－200～－400的脉冲响应值区间；而ΔGINI则在第15期后成为负影响，并呈现逐渐加强的趋势。

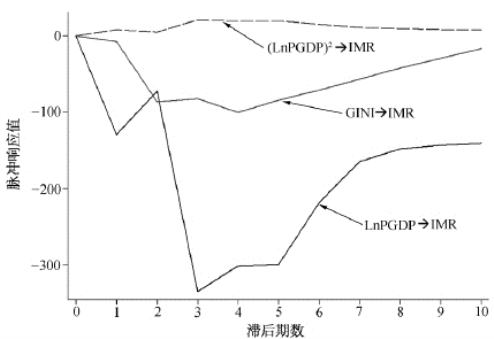
图3-7　基于VAR模型10年滞后期的脉冲响应图

图3-8　基于VAR模型30年滞后期的脉冲响应图

图3-9　基于VEC模型10年滞后期的脉冲响应图

基于VAR模型和基于VEC模型所绘制的脉冲响应图本质上反映了不同空间的情况，与图3-7和图3-8相比，图3-9和图3-10给出的脉冲响应图的实际意义较难解释，原因就是需要在增量空间(可称为gain space，就婴儿死亡率而言，“gain”意指婴儿死亡率下降)进行探讨。图3-7和图3-8反映的是水平空间的变化特征，图3-9和图3-10反映的则是增量空间的变化特征。

在水平空间LnGDP和GINI的影响基本一致，均为负影响，但LnPGDP引起的脉冲响应值总体上要明显高于GINI的影响。而在增量空间，第15滞后期前ΔLnGDP和ΔGINI的影响方向则是相反的，GINI对IMR为正影响，而LnPGDP对IMR为负影响。综合起来看，无论是在水平空间(基于VAR模型的脉冲响应函数)还是在增量空间(基于VEC模型的脉冲响应函数)，既要看到GINI效应区别于LnPGDP的特点，又要注意到LnPGDP效应可能掩盖GINI的独立效应，尽管在本研究所尝试的各类模型中并未提示GINI的独立效应具有显著的统计学意义。

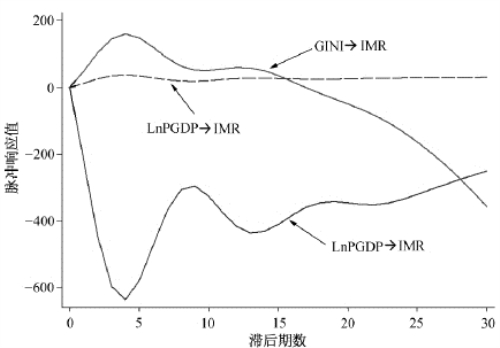
图3-10　基于VEC模型30年滞后期的脉冲响应图

此外，由于脉冲响应图是根据现有VAR模型或VEC模型参数(系数)，在较长(理论上甚至可以无限长)的滞后期内考察脉冲响应值的动态变化，带有较强的预测性，这也构成对本研究所考察的时间序列长度较短(1990～2008年)的一个补充分析。脉冲响应的预测结果，尤其是远期响应值的预测，可以待将来用更长的时间序列数据进行实证检验。