【摘要】：定理2.4.2（积分中值定理）设f（x）在［a，b］上连续，则至少存在一点ξ∈［a，b］，使证 由定理2.4.1知在［a，b］上可导，显然，在［a，b］上也连续，即在［a，b］上连续，在（a，b）内可导，故由Lagrange中值定理得.即即显然，ξ∈［a，b］.实际上ξ在（a，b）内，因此，微分中值定理和积分中值定理的中间点就一致了.而积分中值定理要求f（x）在［a，b］上连续，结论才能成立.例如
定理2.4.2（积分中值定理）设f（x）在［a，b］上连续，则至少存在一点ξ∈［a，b］，使
证 由定理2.4.1知
在［a，b］上可导，显然，在［a，b］上也连续，即
在［a，b］上连续，在（a，b）内可导，故由Lagrange中值定理得
.即
即
显然，ξ∈［a，b］.
实际上ξ在（a，b）内，因此，微分中值定理和积分中值定理的中间点就一致了.而积分中值定理要求f（x）在［a，b］上连续，结论才能成立.例如，对于闭区间［1，2］上的如下分段连续函数f（x）及其原函数F（x），
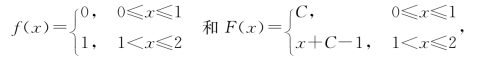
虽然Newton－Leibniz公式是成立的，但定理2.4.2的结论不成立.其实，如果f（x）在［a，b］上可积，且在［a，b］上有原函数，即f（x）在［a，b］上连续，或只有有限个第一类间断点，此时，可定义f（x）在间断点x0处的函数值f（x0）＝
，积分中值定理也是成立的.故此，积分中值定理可推广如下.
定理2.4.2′ 如果f（x）在［a，b］上可积，且在［a，b］上有原函数，则在（a，b）内至少存在一点ξ，使
显然，如果将Newton－Leibniz公式和微分中值定理联系起来，便有
这样，应用起来就方便灵活了.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
