解 A的特征方程为
|A-λE|=
![]()
当λ1=2时,解方程(A-2E)X=O.由
A-2E
![]()
得基础解系p1=
![]()
当λ2=4时,解方程(A-4E)X=O.由
![]()
得基础解系p2=
![]()
例5.1.2 求矩阵A=
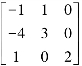
解 A的特征方程为
|A-λE|=
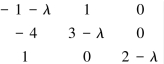
所以A的全部特征值为λ1=2,λ2=λ3=1.
当λ1=2时,解方程(A-2E)X=O.由

得基础解系p1
![]()
当λ2=λ3=1时,解方程(A-E)X=O,由
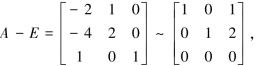
得基础解系p2=
![]()
例5.1.3 求矩阵A=
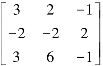
解 A的特征方程为
|A-λE|=
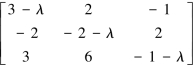
所以A的特征值为λ1=λ2=2,λ3=-4.
当λ1=λ2=2时,解方程(A-2E)X=O.由
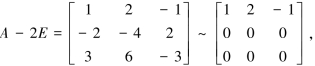
得基础解系p1
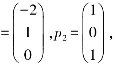
λ2=2的全部特征向量.
当λ3=-4时,解方程(A+4E)X=O.由
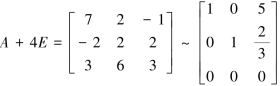
得基础解系p3=
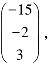
例5.1.4 若λ是矩阵A的特征值,X是A的关于λ所对应的特征向量,证明:
(1)λm是Am的特征值;
(2)当A可逆时,
![]()
(3)当A可逆时,
![]()
证 (1)因为AX=λX,所以
A(AX)=AλX=λAX=λ(AX)=λ2X⇒A2X=λ2X
再继续施行上述步骤多次,就得AmX=λmX,即λm是Am的特征值,X是对应于λm的Am的特征向量.
(2)当A可逆时,λ≠0,因为AX=λX,所以A-1(AX)=λA-1X.
![]()
即A-1X=
![]()
(3)因为AA∗=|A|E,所以A∗=|A|A-1,故A∗X=|A|A-1X=
![]()
![]()
证毕.
5.1.2 特征值与特征向量的有关定理
定理5.1.1 设λ1,λ2,…,λm是A的m个不同的特征值,p1,p2,…,pm依次是与之对应的特征向量,则p1,p2,…,pm线性无关.
证 只证明两个向量的情形:
假设k1p1+k2p2=0⇒A(k1p1+k2p2)=A0=0 ⇒k1Ap1+k2Ap2=0⇒λ1k1p1+λ2k2p2=0 (5.1.3)
另一方面,由条件可得:
λ1k1p1+λ1k2p2=0 (5.1.4)
由式(5.1.3)、式(5.1.4)可得,(λ2-λ1)k2p2=0.
由于p2≠0,λ2≠λ1⇒k2=0,k1=0,故结论成立.
对于多个向量,同理可证.
由定理可知:
(1)属于不同特征值的特征向量是线性无关的;
(2)属于同一特征值的特征向量的非零线性组合仍是属于这个特征值的特征向量.
矩阵的特征向量总是相对于特征值而言的,一个特征值具有的特征向量不唯一,一个特征向量不能属于不同的特征值.
定理5.1.2 设λ1,λ2是A的两个不同的特征值,p1,p2,…,ps;q1,q2,…,ql分别为A的属于λ1,λ2的线性无关的特征向量,则p1,p2,…,ps,q1,q2,…,ql线性无关.
(证明略)
§5.2 相似矩阵及其对角化
5.2.1 相似矩阵
定义5.2.1 设A,B都是n阶矩阵,若有可逆矩阵P,使P-1AP=B,则称B 是A的相似矩阵,或说矩阵A与B相似.可逆矩阵P称为相似变换矩阵,运算P-1AP称为对A进行相似变换.
定理5.2.1 相似矩阵有相同的特征多项式,从而有相同的特征值.
证 设矩阵A与B相似,⇒∃可逆阵P,使得P-1AP=B.
|B-λE|=|P-1AP-P-1(λE)P|=|P-1(A-λE)P|=|P-1||A-λE||P|=|P-1||A-λE||P|=|A-λE|.
即A与B有相同的特征多项式,从而A与B也有相同的特征值,定理得证.
推论5.2.1 若n阶方阵A与对角阵Λ
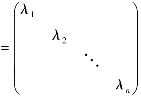
证 因λ1,λ2,…,λn是Λ的n个特征值,由定理5.2.2知,λ1,λ2,…,λn就是A的n个特征值.
由推论可知,若n阶方阵A能与对角阵相似,那么对角阵主对角线上的元素必然就是A的特征值.
利用此推论,若n阶方阵A能与对角阵相似,即P-1AP=Λ,也就是A=PΛP-1,则由P-1AP=Λ,得AP=PΛ.
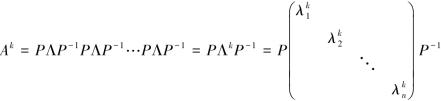
因此利用上述结论计算Ak比直接利用矩阵乘法计算方便得多,特别是针对k较大的情形.
下面要讨论的问题就是:对n阶方阵A,如何寻找相似变换矩阵P,使P-1AP=Λ,即把矩阵A对角化.
5.2.2 矩阵的对角化
定理5.2.2 n阶矩阵A可对角化的充分必要条件是A有n个线性无关的特征向量.
证 假设存在可逆矩阵P,使P-1AP=Λ为对角阵,把P用其列向量表示为P=(p1,p2,…,pn),由P-1AP=Λ,得AP=PΛ,即
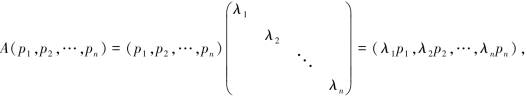
故
A(p1,p2,…,pn)=(Ap1,Ap2,…,Apn)=(λ1p1,λp2,…,λpn).
于是有
Api=λipi(i=1,2,…,n).
可见λi是A的特征值,而P的列向量pi就是A的对应于特征值λi的特征向量.
反之,由于恰好有n个特征值,并可对应地求得n个特征向量,这n个特征向量即可构成矩阵P,使AP=PΛ(因特征向量不唯一,所以矩阵P也是不唯一的,并且可能是复矩阵).又由于矩阵P可逆,所以p1,p2,…,pn线性无关.
命题得证.
由上述定理可知,n阶矩阵A是否可对角化的问题可归结为A是否存在n个线性无关的特征向量的问题.
推论5.2.2 如果n阶矩阵A的n个特征值互不相等,则A与对角阵相似.
若A的特征方程有重根,就不一定有n个线性无关的特征向量,从而不一定能对角化.如A=
![]()
逆矩阵P=
![]()
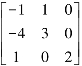
例5.2.1 判断A=
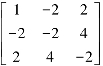
解 由|A-λE|=
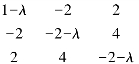
得λ1=λ2=2,λ3=-7.
当λ1=λ2=2时,由(A-2E)X=O,得方程组
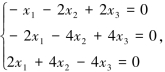
解得基础解系为p1=

同理,当λ3=-7时,解得基础解系为p3
![]()
由于
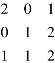
例5.2.2 设A
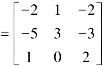
解 |A-λE|=
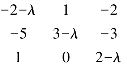
所以特征值为λ1=λ2=λ3=-1.
当λ1=λ2=λ3=-1时,(A-λE)X=O,解得基础解系为
![]()
所以A不能对角化.
§5.3 实对称矩阵的对角化
上一节讨论了矩阵能对角化的充要条件,即:n阶矩阵A能对角化的充要条件是A有n个线性无关的特征向量.通过前面的学习知道,有的n阶矩阵能找到n个线性无关的特征向量,而有的不能找到n个线性无关的特征向量.那么,一个n阶矩阵到底应具备什么条件时才能对角化?这是一个较复杂的问题.我们对此不进行一般性的讨论,而仅讨论当A为实对称矩阵的情形.在给出实对称矩阵可对角化的充分必要条件之前,先介绍3个重要的引理.
引理5.3.1 实对称矩阵的特征值为实数.
(证明略)
引理5.3.2 实对称矩阵的不同特征值对应的特征向量必正交.
证 设λ1,λ2为实对称矩阵的两个不同的特征值,p1,p2是对应的特征向量,则λ1p1=Ap1,λ2p2=Ap2,λ1≠λ2.
因A对称,故A=AT,λ1pT1=(λ1p1)T=(Ap1)T=pT1AT=pT1A.
于是λ1pT1p2=pT1Ap2=pT1(λ2p2)=λ2pT1p2,⇒(λ1-λ2)pT1p2=0.
因λ1≠λ2,故pT1p2=0.即p1与p2正交.
引理5.3.3 若λ是实对称矩阵A的特征方程的k重根,则矩阵A对应于λ的线性无关特征向量恰有k个.
(证明略)
由上面三个引理,可得如下定理:
定理5.3.1 设A是n阶实对称矩阵,则必有正交矩阵P,使
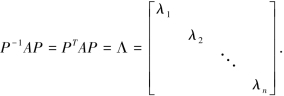
其中,λi(i=1,2,…,n)是A的特征值.
证 设A的互不相等的特征值为λ1,λ2,…,λs,它们的重数依次为r1,r2,…,rs,(r1+r2+…+rs=n).
据引理5.3.1(对称矩阵的特征值为实数)和引理5.3.3可得,对应特征值λi恰有ri(i=1,2,…,s)个线性无关的特征向量,把它们正交化再单位化,得到n个两两正交的单位特征向量,依它们列向量构成正交矩阵P,使PTAP=Λ.其中,Λ的对角线上的元素含r1个λ1,r2个λ2,…,rs个λs,它们是A的n个特征值.
根据上述结论,给出实对称矩阵A寻找正交矩阵P,使PTAP对角化的具体步骤为:
(1)求A的特征值λ1,λ2,…,λn;
(2)求出A的特征向量p1,p2,…,pn;
(3)用施密特正交法把p1,p2,…,pn正交化;
(4)将特征向量单位化.
例5.3.1 设A=

求出正交矩阵P,使P′AP为对角阵.
解 (1)求A的特征值.
|A-λE|=
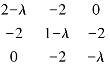
特征值为λ1=4,λ2=1,λ3=-2.
(2)求特征向量
当λ1=4时,由(A-4E)X=O,即
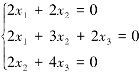
解得基础解系为p1=
![]()
当λ2=1时,由A-E( )X=O,即
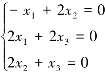
解得基础解系为p2=
![]()
当λ3=-2时,A+2E( )X=O,即
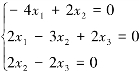
解得基础解系为p3
![]()
(3)由于p1,p2,p3分别是三个属于不同特征值的特征向量,由引理5.3.2知,p1,p2,p3必两两正交.
将特征向量标准化得:
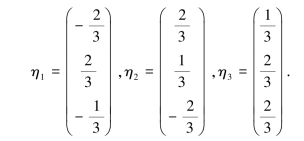
令P=(η1,η2,η3)=
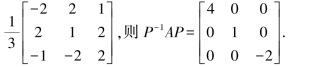
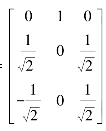
例5.3.2 设A
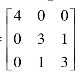
,求一个正交矩阵P,使P′AP为对角阵.
解 |A-λE|=
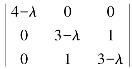
得特征值λ1=2,λ2=λ3=4.
当λ1=2,由(A-2E)X=O,解得基础解系p1=
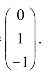
当λ2=λ3=4,由(A-4E)X=O,解得基础解系p2=
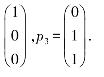
易验证p2,p3恰好两两正交,所以p1,p2,p3两两正交.
将特征向量标准化得η1
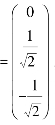
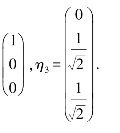
于是得正交阵P=
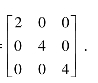
§5.4 二次型及其标准型
在解析几何中,为了便于研究二次曲线ax2+bxy+cy2=1的几何性质,可以选择适当的坐标变换,把方程变化为mx′2+ny′2=1,由此可确定其图形是圆、椭圆还是双曲线,从而方便地讨论原来曲线的图形和性质.
二次曲线ax2+bxy+cy2=1的左边是一个二元二次齐次多项式,经过变换化为左边仅只有平方项的二次齐次多项式,把该问题推广到n元二次齐次多项式,从而建立起二次型理论.
在数学中,二次型的理论起源于解析几何中上化二次曲线和二次曲面方程为标准型的问题,现在二次型的理论不仅在几何而且在数学的其他分支及物理、力学、工程技术中也常常用到。如函数求极值,运输规划,控制理论中判断稳定性问题,统计学上求统计距离,物理上的耦合谐振子问题等都用到了二次型理论.本节先介绍二次型的相关概念及合同矩阵的定义.
5.4.1 二次型的概念
定义5.4.1 含有n个变量x1,x2,…,xn的二次齐次函数
f(x1,x2,…,xn)=a11x21+a22x22+…+annx2n+2a12x1x2+2a13x1x3+…+2an-1,nxn-1xn
称为二次型,只含有平方项的二次型f=k1y21+k2y22+…+kny2n称为标准型.
当aij是复数时,f称为复二次型;当aij是实数时,f称为实二次型.下面讨论的二次型均为实二次型.
例如f(x1,x2,x3)=2x21+4x22+5x23-4x1x3,f(x1,x2,x3)=x1x2+x1x3+x2x3都是二次型;f(x1,x2,x3)=x21+4x22+4x23是二次型的标准型.
为了利用矩阵研究二次型的性质,取aji=aij,则2aijxixj=aijxixj+ajixixj,于是f(x1,x2,…,xn)=a11x21+a22x22+…+annx2n+2a12x1x2+2a13x1x3+…+
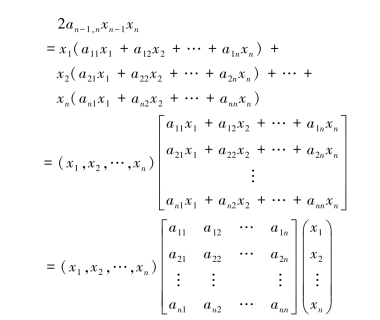
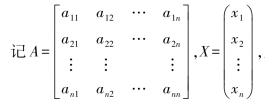
f=XTAX
其中A为对称阵,称为二次型的矩阵,它的秩也称为二次型的秩.例5.4.1 写出二次型f=x21+2x22-3x23+4x1x2-6x2x3的矩阵.解 由题可知,a12=a21=2,a13=a31=0,a23=a32=-3.
故A=
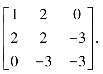
例5.4.2 写出标准二次型f=λ1x21+λ2x22+…+λnx2n的矩阵.
解 显然A=

由上述例子可见,在二次型的矩阵表示中,任给一个二次型,就唯一地确定一个对称矩阵;反之,任给一个对称矩阵,也可唯一地确定一个二次型.这样,二次型与对称矩阵之间存在一一对应的关系.
5.4.2 合同矩阵
对于二次型,我们讨论的主要问题是:是否存在一个可逆的线性变换,能将二次型化为标准型?
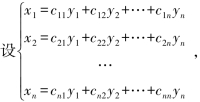
记C=(cij)n×n,Y

f=XTAX=(CY)TA(CY)=YT(CTAC)Y.
令B=CTAC,则有f=YTBY.
因为BT=(CTAC)T=CTATC=CTAC=B,所以B也是一个对称阵,因此f=YTBY也是一个二次型.
因B=CTAC,故R(B)≤R(AC)≤R(A).
又因A=(CT)-1BC-1,故R(A)≤R(BC-1)≤R(B),R(A)=R(B).
由此可知,经可逆变换X=CY后,二次型f的矩阵由A变为CTAC,且二次型的秩不变.也就是说,要使二次型经可逆变换X=CY后变成标准型,只要使CTAC变为对角阵即可.因此,化标准型的过程就是寻找可逆矩阵C使CTAC为对角阵的过程.
定义5.4.2 设A,B是两个n阶方阵,如果存在一个可逆矩阵C,使得B=CTAC,则称A与B是合同的.
因此将二次型转化为标准型的过程就是对二次型的矩阵A(对称阵),寻求可逆矩阵C,使CTAC为对角阵的过程.这个过程称为把对称阵A合同对角化.
§5.5 化二次型为标准型
5.5.1 正交变换法
由定理5.3.1知,任给n阶实对称矩阵A,必有正交矩阵P,使得
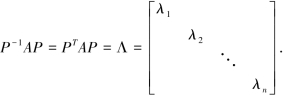
其中,λi(i=1,2,…,n)是A的特征值.而实二次型与实对称存在一一对应关系,因此有下面的定理成立.
定理5.5.1 任给实二次型f=XTAX,总是有正交变换X=PY,使二次型化为标准型f=λ1y21+λ2y22+…+λny2n,其中λi(i=1,2,…n)是A的特征值.
例5.5.1 将二次型f=2x21+x22-4x1x2-4x2x3化为标准型.
解 (1)写出对应的二次型矩阵,并求其特征值

这与例5.3.1给出的矩阵相同,可得特征值为λ1=4,λ2=1,λ3=-2.
(2)由例 5.3.1知存在正交矩阵 P=
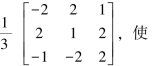
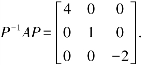
(3)作正交变换X=PY,可把二次型化为标准型f=4y21+y22-2y23.
5.5.2 拉格朗日配方法
用正交变换化二次型为标准形,其特点是保持几何形状不变.那么有没有其他方法也可以把二次型化为标准形?答案是肯定的.下面介绍一种行之有效的方法——拉格朗日配方法.
拉格朗日配方法的步骤:
(1)若二次型含有xi的平方项,则先把含有xi的乘积项集中,然后配方,再对其余的变量同样进行,直到都配成平方项为止,经过非退化线性变换就得到标准型;
(2)若二次型中不含有平方项,但是aij≠0(i≠j),则先作可逆线性变换

化二次型为含有平方项的二次型,然后再按(1)中方法配方.
下面举例说明这一方法的运用过程.
例5.5.2 化二次型f=x21+2x22+5x23+2x1x2+2x1x3+6x2x3为标准型,并求所用线性变换.
解
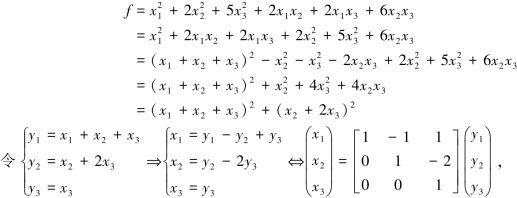
故f=x21+2x22+5x23+2x1x2+2x1x3+6x2x3=y21+y22.
所用变换矩阵为
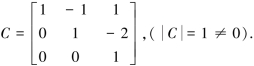
例5.5.3 化二次型f=2x1x2+2x1x3-6x2x3为标准型,并求所用线性变换.
解 由于所给二次型中无平方项,所以令
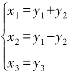
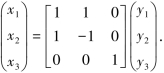
代入f=2x1x2+2x1x3-6x2x3,得f=2y21-2y22-4y1y3+8y2y3.再配方,得
f=2(y1-y3)2-2(y2-2y3)2+6y23.
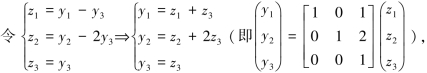
得二次型f的标准型为:f=2z21-2z22+6z23.
其中线性变化矩阵为
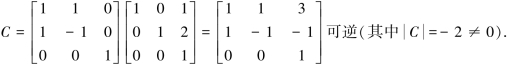
§5.6 正定二次型
在实二次型中,正定二次型占有重要的地位,下面给出正定二次型的定义及常用的判别定理.
定义5.6.1 设有实二次型f(x)=XTAX,如果对任意n维列向量X≠0,都有f(x)>0(显然f(0)=0),则称f(x)=XTAX为正定二次型,并称实对称矩阵A为正定矩阵.如果对于任意n维列向量X≠0,有f(x)=XTAX≥0,则称f(x)=XTAX为半正定二次型,并称实对称矩阵A为半正定矩阵.
例如二次型f=x2+4y2+16z2为正定二次型,一般来说,二次型用定义来判别其正定性往往比较困难,下面给出几种判别方法.
定理5.6.1 实二次型f(x)=XTAX为正定二次型的充分必要条件是其标准型f=λ1y21+λ2y22+…+λny2n的系数λi(i=1,2,…n)全部大于零.
推论5.6.1 实对称矩阵A正定的充分必要条件是A的特征值全为正.
推论5.6.2 若A为正定矩阵,则|A|>0.
事实上,用行列式来判别一个矩阵或者二次型是否正定也是一种常用的方法.设A为n阶对称矩阵,由A的前k行k列元素构成的k阶行列式

定理5.6.2 实二次型f(x)=XTAX为正定二次型的充分必要条件是它的二次型矩阵A的各阶顺序主子式都为正,即
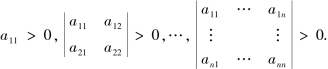
例5.6.1 判断二次型f(x1,x2,x3)=5x21+x22+5x23+4x1x2-8x1x3-4x2x3的正定性.
解 二次型f(x1,x2,x3)的矩阵为A=

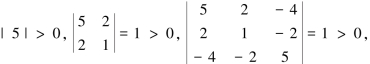
由定理5.6.2知该二次型是正定二次型.
例5.6.2 判断二次型f(x1,x2,x3)=-5x21+2x22-6x23+2x1x2+8x1x3的正定性.
解 二次型f(x1,x2,x3)的矩阵为A=
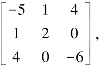
定义5.6.2 设有实二次型f(x)=XTAX,如果对任意n维列向量X≠0都有f(x)<0,则称f(x)=XTAX为负定二次型,并称实对称矩阵A为负定矩阵.如果对于任意n维列向量X≠0,有f(x)=XTAX≤0,则称f(x)=XTAX为半负定二次型,并称实对称矩阵A为半负定矩阵.如果对于任意n维列向量X≠0,有f(x)=XTAX有时为正,有时为负,则称f(x)=XTAX为不定二次型.
定理5.6.3 实二次型f(x)=XTAX为负定二次型的充分必要条件是它的二次型矩阵A的所有奇数阶顺序主子式为负,偶数阶顺序主子式为正.
例5.6.3 判断二次型f=-2x21-6x22-4x23+2x1x2+6x1x3的正定性.
解 二次型的矩阵为A=
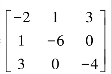
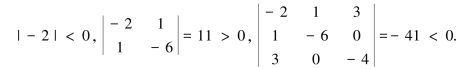
即奇数阶顺序主子式为负,偶数阶顺序主子式为正.
由定理5.6.3知,该二次型是负定的.
例5.6.4 问a取何值时,二次型f=x21+2x22+3x23+2ax1x2-2x1x3+4x2x3是正定的.
解 二次型矩阵为
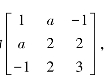
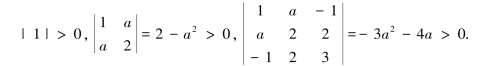
所以

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















