概率的公理化定义

定义1．2．3 设E为随机试验，Ω是它的样本空间，对于E的每一个事件A赋予一个实数，记为P（A），如果集合函数P（·）满足下列条件：

公理一 非负性：对于每一个事件A，P（A）≥0；

公理二 规范性：P（Ω）＝1；

公理三 可列可加性：对于两两互斥的事件A1，A2，…，An，…，即AiAj＝∅（i≠j），有

则称实数P（A）为事件A的概率（probability）．

由概率的公理化定义，可以推出概率的一些性质．

性质1 不可能事件∅的概率为0，即P（∅）＝0．

证 令An＝∅（n＝1，2，…），则

而由P（∅）≥0，故P（∅）＝0．

这个性质说明：不可能事件的概率为0．但逆命题不一定成立．

性质2 有限可加性，若A1，A2，…，An为两两互斥事件，即AiAj＝∅（i≠j），则有

证明 令An＋1＝An＋2＝…＝∅，则AiAj＝∅（i≠j，i，j＝1，2，…）时，因为

性质3 设A，B是两个事件，P（B－A）＝P（B）－P（BA）．

证明 由B＝（B－A）∪BA且（B－A）∩BA＝∅，得P（B）＝P（（B－A）∪BA）＝P（B－A）＋P（BA）．

若A⊂B，则有P（B－A）＝P（B）－P（A）；P（B）≥P（A）．

事实上，由A⊂B，得B＝A∪（B－A），且A（B－A）＝∅，由概率的有限可加性，得P（B）＝P（A∪（B－A））＝P（A）＋P（B－A），即

P（B－A）＝P（B）－P（A）；

又由P（B－A）≥0，得P（B）≥P（A）．

性质4 对于任一事件A，有 P（A）≤1．

因为A⊂Ω，由性质3得P（A）≤P（Ω）＝1．

性质5 对于任一事件A，有

证明 因为A∪A＝Ω，A∩A＝∅，由有限可加性，得

性质6 对于任意的两个事件A，B有

P（Α∪Β）＝P（Α）＋P（（B）－P（ΑΒ）．

特别，若A与B互斥，则有P（A∪B）＝P（A）＋P（B）．

证明 因为A∪B＝A∪（B－AB）且A∩（B－AB）＝∅，AB⊂B，故P（Α∪Β）＝P（Α）＋P（Β－ΑΒ）＝P（A）＋P（B）－P（AB）．

上述公式通常称为概率加法公式，概率加法公式可以推广到多个事件的情形．如对于任意三个事件A，B，C，有

P（A∪B∪C）＝P（A）＋P（B）＋P（C）－P（AB）－P（BC）－P（AC）＋P（ABC）．

一般地，若Ai（i＝1，2，…，n）为任意n个事件，则有

（1）AB＝∅；（2）A⊂B；（3）P（AB）＝．

解 （1）P（B 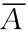）＝P（B－AB）＝P（B）－P（AB）＝；

（2）P（B ）＝P（B－A）＝P（B）－P（A）＝；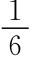

（3）P（B 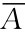）＝P（B－AB）＝P（B）－P（AB）＝

例1．2．2 设A，B为随机事件，且P（A）＝0．7，P（A－B）＝0．3，求

解 ＝1－P（AB）＝1－［P（A）－P（A－B）］＝1－［0．7－0．3］＝0．6．

例1．2．3 设A，B，C为三事件，且P（A）＝P（B）＝，P（C）＝且P（AB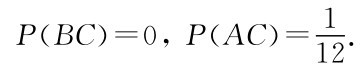）＝求A，B。C至少有一事件发生的概率.

解 P（A∪B∪C）＝P（A）＋P（B）＋P（C）－P（AB）－P（BC）－P（AC）＋P（ABC）