图形几何变换与裁剪

2.2.1 二维图形的几何变换

在二维平面中，构成图形的基本要素是点和线，任何一个图形都可以看成是点的集合，所以点是构成几何形体最基本的元素。而对一个图形进行几何变换，实际上就是对构成图形的一系列顶点进行变换。

二维平面中，点用其两个坐标（x，y）来表示，写成矩阵形式则为［x，y］或。这些矩阵通常被称为点的位置向量。一般的二维图形可以用点的集合来表示，而每个点对应一个向量。如三角形的三个顶点坐标A（x 1，y 1），B（x 2，y 2），C（x 3，y 3），用矩阵表示为这样就建立了二维图形的数学模型。

把二维空间中的任意点A（x，y）变换到一个新的位置A′（x′，y′），数学表达式为

其矩阵表达式为

令则称此矩阵为变换矩阵，即有A′＝A·T。通过这种用一个矩阵和一个变换矩阵施行乘法运算而得到新的矩阵的方法，可以实现二维图形的几何变换，变换矩阵的不同，对应的图形变换也不同。通常二维图形的变换方式有比例变换、对称变换、错切变换、旋转变换、平移变换以及组合变换。

1）比例变换

图形中的每个点以坐标原点为中心，按照相同的比例进行放大或者缩小的变换称为比例变换。设图形在x、y方向上放大或缩小的比例分别为a、d，则变换前后各个点的坐标值满足以下关系：

用矩阵表示为

因此，比例变换矩阵为

如果a＝d＝1，则变换后点的坐标不变，此时变换称为恒等变换。

如果a＝d≠1，则图形将在x、y方向以相同的比例放大（a＝d＞1）或缩小（a＝d＜1），此时变换称为等比例变换。

如果a≠d，则变换后的图形会产生畸变。

2）对称变换

对称变换又称为镜像变换，即变换前后，点对于轴、某一条直线或某一个点。变换前后各点的坐标值满足以下关系：

用矩阵表示为

因此，对称变换矩阵为

如果b＝c＝0，a＝1，d＝－1，则［x′ y′］＝［x －y］，形成关于x轴的对称变换，如图2-2a所示。

如果b＝c＝0，a＝－1，d＝1，则［x′ y′］＝［－x y］，形成关于y轴的对称变换，如图2-2b所示。

如果b＝c＝0，a＝d＝－1，则［x′ y′］＝［－x －y］，形成关于原点的对称变换，如图2-2c所示。

如果b＝c＝1，a＝d＝0，则［x′ y′］＝［y x］，形成关于直线y＝x的对称变换，如图2-2d所示。

如果b＝c＝－1，a＝d＝0，则［x′ y′］＝［－y －x］，形成关于直线y＝－x的对称变换，如图2-2e所示。

图2-2　对称变换

3）错切变换

图形上的每一个点在某一个方向上的坐标保持不变，而在另一坐标方向上进行线性变换，或者在两个坐标方向上都进行线性变换，这种变换称为错切变换。错切变换前后各点的坐标值满足以下关系：

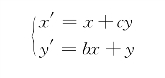
用矩阵表示为

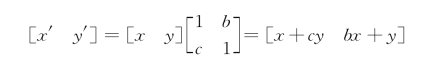
因此，错切变换矩阵为

如果b＝0，c≠0，则有［x′ y′］＝［x＋cy y］，此时图形的y坐标不变。若c＞0，图形沿＋x方向进行错切位移，如图2-3a所示；若c＜0，图形沿－x方向进行错切位移，如图2-3b所示。

如果c＝0，b≠0，则有［x′ y′］＝［x bx＋y］，此时图形的x坐标不变。若b＞0，图形沿着＋y方向进行错切位移，如图2-3c所示；若b＜0，图形沿－y方向进行错切位移，如图2-3d所示。

图2-3　错切变换

4）旋转变换

旋转变换指图形围绕坐标原点旋转θ角的变换，逆时针为正，顺时针为负。旋转变换前后各点的坐标值满足以下关系：

用矩阵表示为

因此，旋转变换矩阵为

5）平移变换

图形的每一个点在给定的方向上移动相同距离的变换称为平移变换。对于一个点的变换，变换前后的坐标值满足以下关系：

用矩阵表示为

［x′ y′］＝［x y］＋［m n］＝［x y］＋T t

显然，在平移变换中，变换前后的原始坐标与变换矩阵是相加关系而不是相乘关系，也就是说，平移变换无法用上述通用变换矩阵相乘的形式来表示。为了将所有图形变换问题表示形式统一起来，以便计算机进行统一处理，这里采用图形的规格化齐次坐标。引入规格化齐次坐标以后，点的平移变换可用矩阵表示为

其中，平移变换矩阵为

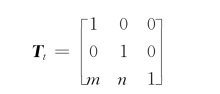
前面介绍的除平移变换外的各种二维变换也可用齐次坐标表示如下：

这样就可以用一个统一的3×3矩阵来描述包括平移变换在内的全部二维图形变换，即

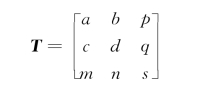
其中产生比例、对称、旋转和错切变换；［m n］产生平移变换产生投影变换，通常在不进行投影变换时取p＝0，q＝0；［s］为全比例因子，使图形产生总体的比例变化，通常取s＝1。

6）二维图形的组合变换

上述图形变换都是相对于坐标轴或坐标原点的基本变换，而CAD/CAE/CAM系统所要完成的任务要复杂得多。工程应用中的图形变换通常是多种多样的，如要求图形绕任意点旋转、图形对任意直线进行对称变换等，需要经过多次基本变换才能完成。由两种及两种以上的基本变换组合而成的变换称为组合变换。将一个复杂的变换分解为几个基本变换，给出各个基本变换矩阵，然后将这些基本变换矩阵按照分解顺序相乘得到相应的变换矩阵，称为组合变换矩阵。

例2-1 设平面三角形ABC，三个顶点坐标分别为A（5，2），B（5，4），C（8，2）。将△ABC绕点P（2，1）逆时针旋转90°，求解变换后各点的坐标及变换矩阵。

解：此变换过程可分为三个基本变换的组合：

首先，将三角形连着旋转中心点P一起平移，使点P和与坐标原点重合，即将三角形沿x轴负方向平移m＝2，沿y轴负方向平移n＝1，其变换矩阵为：

其次，将三角形旋转90°，变换矩阵为

最后，将旋转后的三角形连同旋转中心一起沿x轴正方向平移m＝2，沿y轴正方向平移n＝1，使点A回到初始位置，变换矩阵为

这三个基本变换组合就是使△ABC绕点P逆时针旋转θ＝90°，组合变换矩阵为

△ABC通过T的组合变换后的新三角形为

所以变换后的△A′B′C′各顶点坐标为

A（－1，－7），B（－3，－7），C（－1，－10）

2.2.2 三维图形的变换

三维图形的几何变换是二维图形几何变换的扩展。在进行二维图形的几何变换时，可以用二维空间点的三维齐次坐标及其相应的变换矩阵来表示。同样，在进行三维图形的几何变换时，可以用四维齐次坐标［x y z 1］来表示三维空间点［x y z］，其变换矩阵为4×4阶方阵，通过变换得到新的齐次坐标点，即

［x′ y′ z′ 1］＝［x y z 1］·T

三维图形变换矩阵一般表示为

其中实现图形的比例、对称、错切、旋转等基本变换；［l m n］实现图形的平移变换实现图形的投影变换，通常在不进行投影变换时取p＝0，q＝0，r＝0；［s］为全比例因子，使图形产生总体的比例变化，通常取s＝1。

1）比例变换

空间立体顶点的坐标按规定比例放大或缩小的变换称为三维比例变换。变换矩阵T主对角上的元素a、e、j、s使图形产生比例变换。

（1）令T中非主对角元素为0，s＝1，则变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T s＝［ax ey jz 1］

其中，a、e、j分别为沿x、y、z坐标方向的比例因子。当a＝e＝j＞1时，图形等比例放大；当a＝e＝j＜1时，图形等比例缩小。

（2）令T中主对角元素a＝e＝j＝1，非主对角元素为0，则变换矩阵为

变换后点的坐标为

由此可见，元素s可使整个图形按照相同的比例放大或者缩小。当s＞1时，图形等比例缩小；当0＜s＜1时，图形等比例放大。

2）对称变换

标准三维空间对称变换是相对于坐标平面进行的。

（1）相对xOy坐标平面的对称变换，其变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x y －z 1］

（2）相对yOz坐标平面的对称变换，其变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［－x y z 1］

（3）相对xOz坐标平面的对称变换，其变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x －y z 1］

3）错切变换

三维错切变换是指空间立体沿x、y、z坐标方向都产生错切变形的变换。错切变换是画斜轴测图的基础，其变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x＋dy＋hz bx＋y＋iz cx＋fy＋z 1］

其中，d、h为沿x方向的错切系数；b、i为沿y方向的错切系数；c、f为沿z方向的错切系数。由变换结果可以看出，任何一个坐标方向的变化，均受另外两个坐标方向变化的影响。

4）平移变换

平移变换是使空间立体在三维空间移动位置而形状保持不变的变换，其变换矩阵为

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x＋l y＋m z＋n 1］

其中，l、m、n分别为沿x、y、z坐标方向上的平移量。

5）旋转变换

旋转变换是将空间立体绕坐标轴旋转角度θ的变换。θ角的正负按右手定则确定：右手大拇指指向旋转轴的正向，其余四个手指的指向即为θ角的正向。

（1）绕x轴旋转：

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x y cosθ－z sinθ y sinθ＋z cosθ 1］

（2）绕y轴旋转：

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x cosθ＋z sinθ y z cosθ－x sinθ 1］

（3）绕z轴旋转：

变换后点的坐标为

［x′ y′ z′ 1］＝［x y z 1］·T＝［x cosθ－y sinθ x sinθ＋y cosθ z 1］

2.2.3 三维图形的投影变换

把三维坐标表示的几何形体变成二维图形的过程称为投影变换。投影变换可以分为平行投影和透视投影，当投影中心和投影面之间的距离为无穷远时，投影线为一组平行线，这种投影称为平行投影，如图2-4a所示；当投影中心与投影面之间的距离为有限值时，投影线交于一点，这种投影称为透视投影，如图2-4b所示。平行投影又可分为正平行投影和斜投影，正平行投影可获得工程上的三视图和正等轴测图。

图2-4　投影变换示意图

1）正平行投影变换

投影方向垂直投影平面的投影称为正平行投影。正视图、俯视图和侧视图均属于正平行投影，如图2-5所示。

图2-5　正平行投影变换

（1）主视图变换矩阵。主视图的投影线平行于y轴，xz平面上的y坐标为0，变换矩阵为

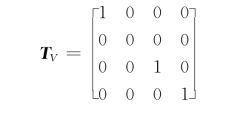
变换结果为

［x′ y′ z′ 1］＝［x y z 1］·T V＝［x 0 z 1］

（2）俯视图变换矩阵。俯视图的投影线平行于z轴，xy平面上的z坐标为0。为了使俯视图和主视图同画在xz平面上，并与主视图有一定的距离d，需要将H平面的正投影先绕x轴旋转－90°，再沿－z方向平移d，于是俯视图的变换矩阵为

变换结果为

［x′ y′ z′ 1］＝［x y z 1］·T H＝［x 0 －y－d 1］

（3）左视图变换矩阵。左视图的投影线平行于x轴，yz平面上的x坐标为0。为了使左视图和主视图同画在xz平面上，并与主视图有一定的距离l，需要将W平面的正投影先绕z轴旋转＋90°，再沿－x方向平移l，于是左视图的变换矩阵为

变换结果为

［x′ y′ z′ 1］＝［x y z 1］·T W＝［－y－l 0 z 1］

2）正轴测投影变换

正轴测投影，也称为正轴测图，它是一种立体图，能够直观地表达物体的三维形状。若将图2-6a所示的立方体直接向V面投影，就得到图2-6b；如果将立方体绕五轴旋转θ角，再向V面投影，就得到图2-6c所示的图形；如果将立方体先绕z轴旋转θ角，再绕x轴旋转－φ角（φ＞0），最后再向V面投影，就得到图2-6d所示的立方体的正轴测投影图。

图2-6　正轴测投影图的生成过程

变换矩阵为

以上是一个正轴测投影变换的一般形式，在应用中，只要任意给定θ、φ的值，就可以得到不同的正轴测投影图。正轴测投影图主要分为正等轴测图和正二等轴测图。

（1）正等轴测投影。按国家标准规定，以θ＝45°、φ＝35°16′带入上式中，即可得到正等轴测投影变换矩阵

（2）正二等轴测投影图。按国家标准规定，以θ＝20°42′、φ＝19°28′带入上式中，即可得到正二等轴测投影变换矩阵

3）透视投影变换

透视图是采用中心投影法得到的图形，这种投影是将投影面置于投影中心与投影对象之间，通过投影中心（视点），将空间立体投射到二维平面上所产生的图形。

（1）透视变换矩阵。在前面介绍的4×4三维图形几何变换矩阵中，第四列元素p、q、r为透视参数，赋予它们非零值将产生透视效果。在讨论透视变换时，一般不考虑全比例变换参数s的影响，故

变换结果为

若p、q、r三个元素中有两个为零，则得到一点透视变换；若p、q、r三个元素中有一个为零，可得到两点透视变换；若p、q、r三个元素均不为零，则可得到三点透视变换。

（2）一点透视变换。进行一点透视变换时，物体沿某一方向相互平行的一组棱线在透视图中不再平行，其延长线的交点称为灭点。一点透视只有一个灭点。透视变换矩阵中的元素p、q、r只有一个不为零，可获得一点透视效果。

y轴上有灭点的一点透视变换的具体步骤为：

①将物体平移到适当的位置，一般置于画面后。

②对物体进行一点透视变换。

③将物体向V面投影。

因此，y轴上有灭点的一点透视投影变换矩阵为

同理可推出x、z坐标轴上分别具有一个灭点的一点透视变换矩阵。

（3）两点透视变换。如前面介绍，只要透视变换矩阵中的三个元素p、q、r中有一个为零，其余两个不为零，就可得到具有两个灭点的透视变换。设p≠0、q≠0、r＝0，两点透视投影图可用下面两种方法求得。

方法一：先将物体平移，以旋转合适的视点，然后进行两点透视变换，再将物体绕z轴旋转θ角［θ＝arctan（p/q）］，最后向V面投影。此时，两点透视变换矩阵为

方法二：先将物体平移，然后使物体绕z轴旋转θ角（一般为30°或60°），以使物体的主要平面与画面成一定角度，再进行透视变换，最后向V平面投影。此时，两点透视变换矩阵为

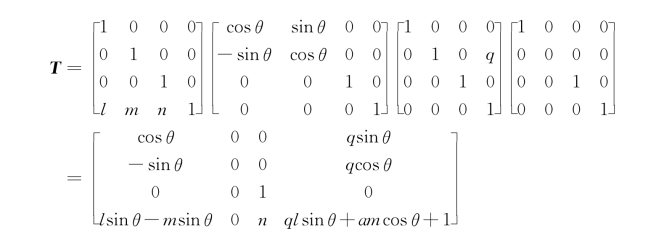
（4）三点透视变换。三点透视即为具有三个灭点的透视，透视变换矩阵中的元素p、q、r均不为零。获得三点透视的方法也有两种。

方法一：将物体平移到合适位置，接着用透视变换矩阵对物体进行透视变换，然后使物体先绕z轴旋转θ角，再绕x轴旋转－φ角（φ＞0），最后将旋转后的物体向V面投影，即可得到三点透视投影图。其透视投影变换矩阵为

方法二：将物体平移到适当位置，接着将物体先绕z轴旋转θ角，再绕x轴旋转－φ角（φ＞0），然后进行一点透视，最后向V面投影即可得到三点透视投影图。其透视投影变换矩阵为

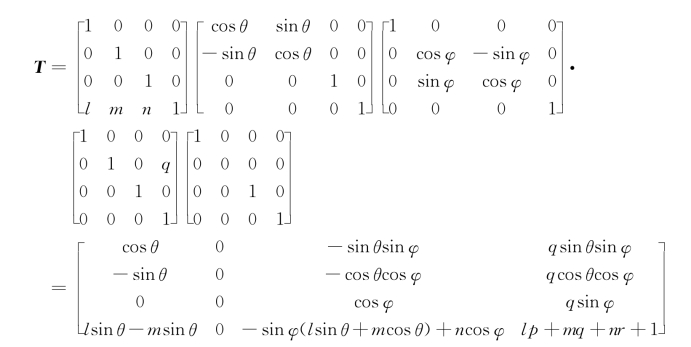
尽管上面这两种形式不同，但其本质是一样的。

2.2.4 图形的裁剪

裁剪是指以窗口为边界，将图形分为可见区域和不可见区域，仅保留窗口内的可见部分，去掉窗口外的不可见部分，并将可见部分在计算机显示器等图形输出设备上输出，把这种识别和选择可见图形信息的方法称为图形的裁剪。

利用裁剪技术可以将窗口内的图形信息和窗口外的图形信息区分开来，裁剪的边界可以是任意多边形，但常用的是矩形。被裁剪的对象可以是线段、字符、多边形等。

裁剪类型可以分为二维裁剪和三维裁剪两种基本类型，下面重点讨论二维图形中的点和线段的裁剪问题。

1）点的裁剪

由于任何图形都可以看作点的集合，因此点的裁剪是其他图形裁剪的基础。假设窗口x坐标的界限值为x min和x max，y坐标的界限值为y min和y max，则当一点判定为可见时，必须同时满足下列两个不等式约束：

若其中任一条件不满足，则该点为不可见点。

根据点的裁剪原理，二维图形的裁剪可以采用一种最简单的裁剪方法，即逐点比较法，也就是逐点比较图形上的各点是否满足上述条件，并将不可见点裁剪掉。从理论上来说，这是一种“万能”的裁剪方法，但是逐点比较法实际上没有使用价值。因为一方面，将图形离散成点需要大量的时间，算法的运行速度太慢；另一方面，这样裁剪得到的点不能保存原有图形的画线序列，给图形的输出造成困难，所以有必要研究高效的裁剪方法。

2）二维线段的裁剪

任何图形都可以看作是由直线段组成的，曲线、圆弧也可以用直线段来逼近，因此二维线段的裁剪是二维图形裁剪问题的基础。

线段裁剪的任务就是要确定其是完全可见的、部分可见的或者完全不可见的。进行线段裁剪，首先要确定它与窗口边界的相对位置。由于矩形窗口是一个凸多边形，一条直线段的可见部分最多为一段，因此可通过判断两个点的可见性来确定直线段的可见部分。如图2-7所示，一条直线段相对于窗口，其端点有以下几种情况：

①直线段的两个端点都在窗口内，如直线段b。此时不需要裁剪，应全部显示。

图2-7　直线与窗口的相对位置

②直线段的两个端点都在窗口外，如直线段a、d、e和f。其中对于直线段a和e，它们均被窗口边界分成三段，中间一段落在窗口内，应予以显示；对于直线段f，它与窗口边界只有一个交点，此时的可见部分已退化为一个点；而对于直线段d，由于它与窗口的边界不相交，应当被裁剪掉。

③直线段的一个端点在窗口内，而另一个端点在窗口外，如直线段c。需要求出直线段c与窗口边界的交点，并以此为边界将直线段分为两段，然后显示落在窗口内的那一段。

上述各种情况都要通过一定的规则来判别，最常用的方法是编码裁剪算法和中点分割裁剪算法。

图2-8　Cohen-Sutherland编码

（1）编码裁剪算法。编码裁剪算法是1974年Dan Cohen和Ivan Sutherland提出的，所以称Cohen-Sutherland算法，其主要思想是用编码方法来实现裁剪。如图2-8所示，首先用窗口的边界直线将平面分成9个区域，每个区域用4位二进制码来表示，称为“区域码”，4位编码自左向右的意义为

第1位：用1表示点在窗口之上，否则为0；

第2位：用1表示点在窗口之下，否则为0；

第3位：用1表示点在窗口之右，否则为0；

第4位：用1表示点在窗口之左，否则为0。

因此，通过比较线段端点的坐标（x，y）与裁剪窗口的边界，可以生成线段端点的4位二进制“区域码”。具体方法如下：

若满足y＞y max，则区域码的第1位为1，否则为0；

若满足y＜y min，则区域码的第2位为1，否则为0；

若满足x＞x max，则区域码的第3位为1，否则为0；

若满足x＜x min，则区域码的第4位为1，否则为0。

任何一条直线两个端点的编码都与它所在的区域相对应。根据上述编码可知，如果两个端点的编码都为“0000”，则线段全部位于窗口内；如果两个端点的编码“按位与”不为0，则整条线段必位于窗口外。

如果线段不能由上述两种测试决定，则必须把线段再分割。简单的分割方法是计算出线段与窗口某一边界（或边界延长线）的交点，再用上述条件判别分割后的两条线段，从而舍去位于窗口外的一段。如图2-9所示，用编码裁剪算法对线段AB进行裁剪，可以在C点分割，分别对AC、CB进行判别，舍弃AC；再分割CB于点D，对CD、DB进行判别，舍弃CD；而DB全部位于窗口内，算法结束。

需要说明的是，分割线段的过程是先从C点或D点开始是随机的，不影响算法结果。

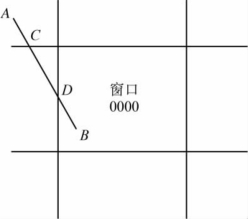
图2-9　编码裁剪算法

图2-10　中点分割裁剪算法

（2）中点分割裁剪算法。由于编码裁剪算法需要计算直线段与窗口边界的交点，因此不可避免地要进行大量的乘除运算，势必降低裁剪效率。而中点分割裁剪算法不用进行大量的乘除运算。

中点分割裁剪算法的基本思想是：分别寻找直线段两个端点各自对应的最远的可见点，两个可见点之间的连线就是要输出的可见段。如图2-10所示，以找出直线段P1 P2上距离P 1最远的可见点为例，说明中点分割裁剪算法的步骤：

①判断直线段P 1P 2是否全部在窗口外，如果是，则裁剪过程结束，无可见线段输出，如图2-10中的线段a；否则，继续上述步骤。

②判断P 2点是否可见，若可见，则P 2点即为距P1点最远的可见点，如图2-10中的线段b；否则，继续步骤③。

③将直线段P1 P2对分，中点为Pm，如果PmP 2全部在窗口外（图2-10中的线段d），用P 1Pm代替P 1P 2；否则，用PmP 2代替P 1 P 2（图2-10中的线段e），然后对新的P 1 P 2从头开始重新判断。

重复上述过程，直到PmP 2小于给定的误差为止（即认为已于窗口的一个边界相交）。把线段两个端点对调一下，即可找出另一个端点P 2的最远的可见点。

由于中点分割裁剪算法只需要进行加法和除2运算，而除2运算在计算机中可以很简单地用右移一位来完成，因此，该算法特别适用于用硬件来实现。相对于编码裁剪算法来说，裁剪速度增快很多。