河床阻力理论分析

5.3　河床阻力理论分析

5.3.1　二维明渠水流理论分析

不可压缩流体遵守Navier-Stokes方程：

式中　t——垂线上某点的流速；

　u——流速；

　f——流体所受外力；

　P——压强。

式中　u′——水流方向的脉动流速；

　v′——垂直于水流方向的脉动流速；

　υ——水的运动黏性系数；

　H——水深；

　y——垂线上某点到槽底的距离；

　θ——渠道的倾角；

u_*——摩阻流速。

紊流边界层或明渠紊流中紧贴壁面的流动曾经被称为层流底层。后来，由流动显示发现，所谓的层流底层中也存在紊流脉动，这一区域应当准确地称为黏性底层。但是黏性底层是紧贴壁面的很薄区域，通常定义为Y^＋＜5，如果紊流边界层的Re_δ＝10 000，黏性底层厚度约为边界层厚度的1/100，假如边界层等于10 mm，则黏性底层厚度大约只有0.1 mm。Kim等（1987年）用128³的空间分辨度对明渠紊流进行直接模拟，离壁面最小的无量纲尺度可以达到Y^＋＝0.05^[135]。

由式（5.5），明渠均匀紊流中应力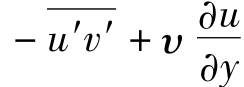沿水深为线性分布。由于流速梯度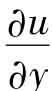只是在壁面附近较大，而在距壁面较远处迅速减小，即黏性切应力在切应力中所占比例随距壁面距离的增加而迅速减小，可见雷诺切应力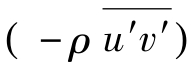在断面上的分布除壁面附近区域外，为线性分布。Neza＆Rodi实测明渠紊流中切应力在断面上的分布^[136]，认为不管是哪一种流动情况，在距壁面一定距离后，雷诺切应力呈线性分布。

5.3.2　大比降粗颗粒河床流速分布

根据Karman的紊流相似假说，紊流的剪力场与流速场之间存在如下关系^[137]：

联解式（5.5）、式（5.6）得：

在床面光滑时，y₀∝u/u_*，如图5.3（a）所示；在床面粗糙时，y₀∝K _s，如图5.3（c）所示。

第3章关于内流河的调查结果分析表明，内流河的河床组成较粗，比降较大，其床面一般为粗糙床面。粗糙壁面紊流的理论床面并不在凸出物的最高平面，而是最高平面以下的某个地方，式（5.7）可变成式（5.2）。内流河床面的流速分布可表达为：

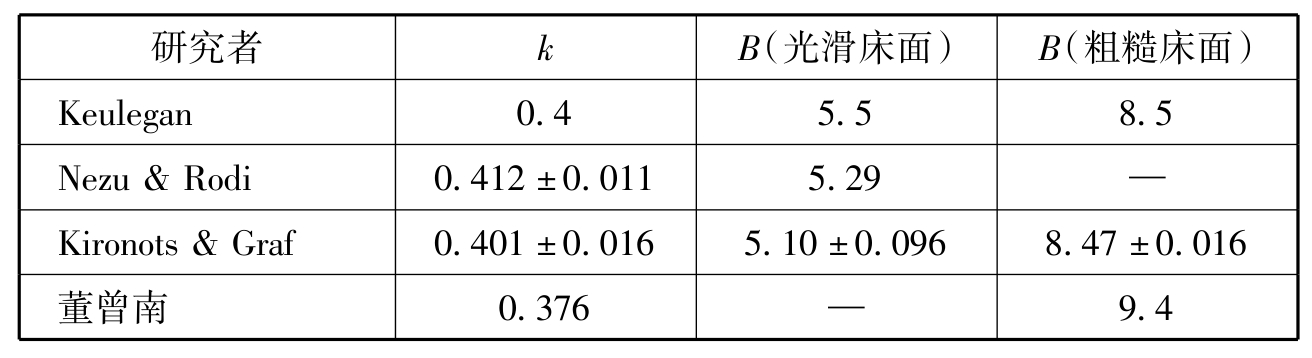
各学者由于资料不同确定的k，B值略有差异，见表5.2所列。

表5.2　各学者确定的k，B值

5.3.3　床面糙率与流速分布的关系

根据曼宁公式：

式中　V——断面平均流速；

　g——重力加速度；

　R——水力半径；

　J——河床比降；

　n——糙率。

从量纲上考虑，n应与某一特征长度的1/6次方成正比。在床面没有泥沙起动时，假设这个特征长度为糙率尺寸，即：

其中，A为常数。

式（5.9）是实际应用曼宁公式表达粗颗粒河床的定床阻力时，用得较多的表达式。曼宁系数n与垂线流速分布的转换关系为：

联解式（5.2）、式（5.9）和式（5.10）得：