第节，基础解系的概念及其求法

时间：2024-09-17 百科知识版权反馈

【摘要】：n个未知数的齐次方程组恒有解。当有非零解时，由于解向量的任意线性组合仍是该齐次方程组的解向量。则称为方程组一个基础解系。所谓基础解系，其实就是的解向量组的一个极大无关组。基础解系的性质设是的基础解系，即是的解。的任一解都可以由线性表出。因为，所以也可以取为自由变量，然后赋值求解。

(1/3) 线性方程组的解空间

n个未知数的齐次方程组恒有解（必有零解）。当有非零解时，由于解向量的任意线性组合仍是该齐次方程组的解向量。因此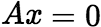的全体解向量构成一个向量空间，称为该方程组的解空间，解空间的维数是。

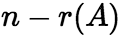(2/3) 基础解系

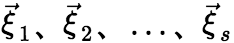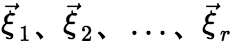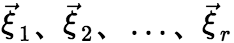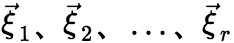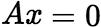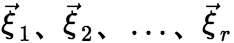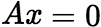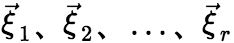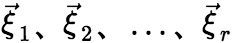（1）基础解系概念：设是方程组的个解向量，则对任意的，向量仍是方程组的解向量。若是方程组的个解向量，并且满足：（i）线性无关。（ii）方程组的任意解向量都可由线性表示。则称为方程组一个基础解系。所谓基础解系，其实就是的解向量组的一个极大无关组。 (2) 基础解系的性质设是的基础解系，即（i）是的解。（ii）线性无关。（iii）的任一解都可以由线性表出。

(3/3) 基础解系的求法

(1) 在求基础解系时，可对A作初等行变换变换成为阶梯形矩阵. (2) 通常称每个非零行中第一个非0系数所代表的未知数是主元（共有个主元），那么剩余的其他未知数就是自由变量（共有个），当然也可在加减消元后找出秩为的行列式，那么其他各列的未知数就是自由变量. (3) 对自由变量按阶梯形赋值后，再代入求解就可以得到基础解系。注：一定是对矩阵进行初等行变换例：若某齐次方程组经高斯消元化为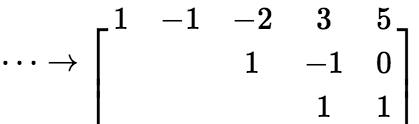则=5-3=2，说明基础解系由2个解向量组成，此时为主元，是自由变量，因而可对自由变量赋值再由下往上代入求得，即为的基础解系。因为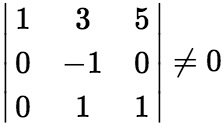，所以也可以取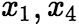为自由变量，然后赋值求解。