由教科书的例

二、由教科书的例、习题进行变式，深入挖掘例、习题的教育功能

1．概念定理变式

概念、定义、定理本身是教科书中的“显性知识”。概念、定义、定理蕴涵着教科书中的“隐性知识”，是形成学生的思维能力、分析和解决问题的能力以及创新精神和实践能力的基础。在复习过程中，通过多样化的变式，可以使学生全面、深入地理解概念、定义、定理的意义和适用范围，灵活、准确地运用概念、定义、定理分析问题和解决问题。

例如在导数几何意义的复习教学中，可以进行如下的变式练习

例：已知曲线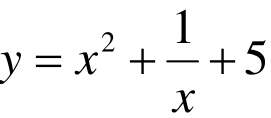上一点P(2,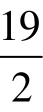)，求点P处的切线方程。

变式1：（2006年四川高考卷文3）曲线y＝4x－x ³在点（－1，－3）处的切线方程（　）

（A）y＝7x＋4（B）y＝7x＋2（C）y＝x－4（D）y＝x－2

变式2：（2004湖北）与直线2x－y＋4＝0平行的抛物线 y＝x ² 的切线方程是（　）

（A）2x－y＋3＝0（B）2x－y－3＝0（C）2x－y＋1＝0

（D）2x－y－1＝0

变式3：已知曲线C：f(x)＝x ³－3x ²＋2x＋a的一条切线方程为y＝2x，求实数a的值。

变式4：曲线y＝－x ³＋1 过点P（－1，1）的切线方程是______________________。

变式5：曲线y＝x ³－x＋2，求经过点P（1，2）的曲线的切线方程为___________________。

变式6：点P在曲线y＝ 2x ³ － x＋1上运动时，在P点处切线的倾斜角的取值范围是___________________。

变式7：已知两条曲线 y＝x ²－1与 y＝1－x ²，（1）这两条曲线在x＝x ₀ 动点处切线互相平行，求X₀的值；（2）这两条曲线在x ＝x ₁ 的动点处的切线互相垂直，求X₁的值。

变式8：已知曲线y＝2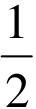－ x ²与y＝ x ³－2在交点处的切线夹角是__________________。

变式9：已知曲线C₁：y＝x ²＋2 ， 曲线C₂：y＝-x ² 是否存在直线L与 C₁、C₂ 都相切？若存在，求出直线方程；若不存在，说明理由。

变式10： P为曲线y＝x ³ 上的一动点，若曲线在该点处的切线与曲线有另一个交点Q，求PQ中点的轨迹方程。

变式11：若方程 x ³-3x-m＝0 有一个二重根，求方程的解集。

变式12：已知y＝kx与y＝lnx有公共点，求k的最大值是_______________。

“变式”，可使学生理解切线的斜率值是切点处导数值。求切线斜率的关键是切点坐标的确定，导数和曲线切线斜率有密切联系，凡涉及函数曲线的切线问题时，注意导数几何意义的应用，但要注意，只有切点处导数值才是切线斜率值。

2．思维变式

对同一问题引导学生进行思维变式从多个角度去分析问题，多角度观察问题，形成各种不同的思路，不同的方法，实现一题多解。可以拓展学生的思维视野，使学生领略人类思维的伟大力量。逐步培养学生的创新意识，创新能力。

此外，很多数学问题都是“貌离神合”。如果应用“变式”展示，貌似不同的问题，实质为同一解法。不仅有利于激发学生的学习兴趣，更有利于学生理解方法的实质，掌握“最关键的方法”，起到“事半功倍”的效果。

例：求y=−x ²−4x+1，x∈[−3,3]的最大值、最小值。

变式1：求函数y=9sin₂ x−12conx−8的最大值、最小值。

变式2：求函数y=sinx+conx+sinxconx的最大值、最小值。

变式3：已知，等差列{a _n}满足S₁₂＞0，S₁₃＜0且a ₁＞0，求前n项和Sn的最大值。

变式4：已知，y=lnxln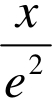−3(1<x≤e ²)，求y的最大值、最小值。

变式5：已知，△ABC中，∠A=，AB＝1，AC＝2，点P在边BC上运动，求• 的最大值、最小值。

这一组题，看似各不相同、差异很大，实质都可用二次函数的图像和性质求解。

3．小题大做式变式

解决一类问题，观察、分析、归纳概括出本质特征，形成相应的方法运用模式，不仅有利于知识结构的完善，也有利于高效率地进行解法的选择，迅速有效地解决问题。

例：教科书第一册上第119页，等差数列前n项和公式推导方法：“倒序相加法”

变式1：已知数列a₁，a₂，a₃，5，a₅……，75，a_n－2，a_n－1，a_n是等差数列，则其所有项和S_n＝___________________

变式2：已知数列｛a _n｝满足m＋n＝p＋g则a_m ＋ a_n ＝a_p ＋a_g 的条件， a ₁＝M， a _n＝ N，其前n项和S_n＝_____________________

变式3：函数f(x)＝ 求f(－5)＋f(－4)＋…＋f(0)＋…＋f(5)＋f(6)的值为_______________________________

变式4：函数f(x)满足f(x)＋f(a－x)＝b，a∈Z则f(a－6)＋ f(a －5)＋ f(a－4) ＋……＋f(4)＋ f(5)＋ f(6)＝_____________________

这一组变式可以引导学生概括出：满足x ₁＋x₂＝x₃＋ x₄，则f (x₁) ＋ f (x₂)＝ f (x₃)＋ f (x₄) 的性质的函数值求和都可考虑用“倒序相加法”，再具体一点可以是：满足存在一个常数a，使f(x)＋f(a －x) 为常数的函数值求和，都可以考虑使用“倒序相加法”。

4．大题小做式变式

综合题的求解，学生往往感到无从下手，如果老师对问题进行分拆、变式，先用一些基础问题形成铺垫 ，引导学生拾阶而上，最终克服困难解决问题。不仅能调动学生学习的主动性，更有利于学生能力的形成。

由高中数学第二册上第106页例3变式可得：

变式1:已知两定点F₁(−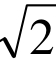,0) ，F₂(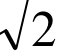,0)，且||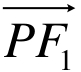－||＝2 ，求P点的轨迹方程。

由高中数学第二册上第118页例3变式可得：

变式2：已知直线y＝kx－1与曲线x ²－y ²＝1（x＜0）交于两点A、B，且|AB|＝6，求直线AB方程。

由高中数学第一册下第106页例4变式可得：

变式3：已知直线方程y＝kx－1与曲线方程x ²－y ²＝1（x＜0）交于两点A、B，且AB的中点为D，O为原点，求OD的方程。

由高中数学第二册上第50页例8变式可得：

变式4：已知＋＝，D为AB的中点，用表示。

由高中数学第一册下第150页复习参考题五A组第18题变式可得：

变式5：已知直线方程y＝kx－1与曲线方程x ²－y ²＝1（x＜0）交于AB两点，点C在曲线上，且＋＝，求点C的坐标。

综合上述五题构造变式可得：

变式6：（2006年四川高考题　理21，文22）已知F₁ (− ,0) ， F2( ,0)，满足||－||＝2的点P的轨迹是曲线E，直线y＝kx－1与曲线E交于A、B两点，如果|AB|＝6，且曲线E上存在点C，使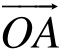＋＝，求m的值和△ABC的面积S。

这样的变式可以根据学生的实际，调整变式的梯度，在学生的“最近发展区”设计问题，使学生既易于入手又有思考的空间，从而激发学生的学习热情，培养学生的能力。

5．一题多问变式

采用一题多问变式，可以引导学生对相关概念和方法，从多种角度分析、思考，利于学生深入理解概念，深刻领会方法。

例:设z＝2x＋y，式中变量x，y满足下列条件：

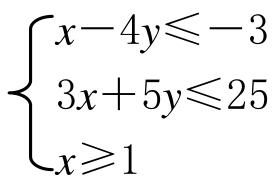
求Z的最大值和最小值。

变式1：求的最大值，最小值。

变式3：求x²＋y²的最大值，最小值。

变式4：求x²＋4y²的最大值，最小值。

变式5：求的最大值，最小值。

变式6：若点P (a⋅cosθ+3,a⋅sinθ+2)为可行域内点，求a的取值范围。

6．多题一问式变式：

采用多题一问式变式，可以引导学生对相关方法进行多角度分析、概括，领会方法的实质，体验方法应用中注意的问题。

例如：（教科书第一册上第43页复习参考一B组2题）

已知A＝｛ x||x－a|＜4｝，B＝｛x || x －2|＞3｝，且A∪B＝R 求a的范围。

变式1：已知A＝｛ x||x－a|＜4｝，B＝｛x || x －2|＞3｝且A∩B＝A，求a的范围。

变式2：已知A＝｛ x||x－a|＜4｝，B＝｛x || x －2|＞3｝且x∈A是x∈B的充分非必要条件，求a的取值范围。

变式3：已知A＝｛ x||x－a|＜4｝，B＝｛x || x －2|＞3｝x∈A，x∈B有且仅有一个成立，求a的取值范围。

A　a＜0；　 B　a＝0；　 C　0＜a＜1；　 D　 a≥1。

变式5：点A（1，a），B(a，－1)在直线x－y＝0两侧求a的取值范围。

变式6：已知f（x）是定义在（－1，1）上的奇函数，且在（－1，1）上，恒有f ^/(x)＞0，若f（a－1）＋ f（a）＞0则a的取值范围是________________。

变式7：已知函数y＝ x ³＋ax＋b在区间（－1，0），（0，1）上各有一个极值点，求a的取值范围。

变式8：关于x的不等式x ²－4x≥a，对x∈（0，1）桓成立，则实数a取值是______________________。

变式9：点A(3cosα，3sinα，1)，B (2cosθ，2sinθ，1)， ||=a，则a的取值范围是_______________。

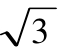变式10：点A(cosα，sinα，)，B (cosθ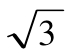，sinθ， 1)，O为空间直角坐标系的原点，a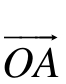＝＜，＞，则a的取值范围是_____________________。

变式11：在△ABC中，∠A＝，AB＝1，AC＝2，P为△ABC边上的一动点，a＝，则a的取值范围是______________________。

变式12：请同学们自己设计一个求a的范围的问题。

这一组变式，可以引导学生概括出：范围问题的解法主要有三种：一是依据题意构造不等式或不等式组求解；二是构造相应函数而求解；三是“数形结合”观察、分析而求解。

7．方法运用变式

数学“常用解题方法”都有一定的适用范围。运用变式可引导学生总结方法的适用范围及相应的补救解法，可以培养学生准确选用方法和灵活运用方法的能力。

例：第128页习题3．6第2题)求函数y=x ³−x ²−x的单调区间。

变式1：讨论函数y=x ²− x+3(x∈N ^∗)的单调性。

变式2：(2006年陕西卷文数22)设函数

f(x)=kx ³−3x ²+1(k≥0)，求函数f(x)的单调区间。

变式3：(2006(全国卷)^I文数22题)设a为实数，

f(x)=x ³−ax ²+a ²−1x在(－∞，0)和(1，＋∞)都是增函数，求a的取值范围。

变式4：定义在N ^∗上的函数y=n ²−an是增函数，则a的取值范围是(　)

(A )a＞2；　(B)a＜2；　(C)a＞3；　(D)a＜3。

变式5: 定义在N ^∗上的函数f(x)满足且为增函数，则a的取值范围是(　)

(A ) a＞2；　(B)a＜2；　(C)a＞3； (D)a＜3。

这一组变式，可以引导学生总结出：运用导数解决函数的单调性问题是常用、有效的方法。但，对抽象函数和定义域为间断点集的函数一般不适用，要注意选用“数形结合”等其他方法求解。