差分方程简介

在经济管理及其他实际问题中，许多数据都是以等间隔时间周期统计的．这些离散取值的变量通常称为离散型变量．描述离散型变量之间关系的数学模型称为离散型模型，而差分方程是研究离散型模型的有效方法．

定义1　设自变量x取离散的等间隔的非负整数值：x＝0，1，2，…，y＝f（x）是x的函数，显然，函数的取值是一个数列

f（0），f（1），…，f（x），f（x＋1），…

简记为

y0，y1，…，yx，yx＋1，…

当自变量从x变到x＋1时，函数的改变量称为函数在点x的一阶差分，记为Δyx，即

例1　设yx＝x2，求Δyx．

解

解

由定义容易得到差分的四则运算法则：

（4）

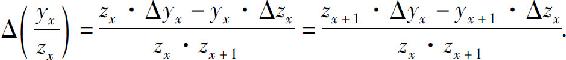
我们只给出式（3）的证明：

类似可证

下面给出高阶差分的定义：

定义2　当自变量从x变到x＋1时，一阶差分的差分

称为函数y＝f（x）二阶差分，简记为Δ2yx，即

同样，二阶差分的差分Δ（Δ2yx）称为三阶差分，记为Δ3yx，即

一般地，y＝f（x）的n阶差分为

一般地，n次多项式的n阶差分为常数，而n阶以上差分均为零．

定义3　含有自变量、未知函数及未知函数差分的函数方程称为差分方程．

其一般形式为

由差分的定义和性质可知，上述差分方程的不同表达式之间可以互相转化．

故原方程可化为

方程中未知函数的最大下标与最小下标的差称为差分方程的阶．

如果把函数yx＝φ（x）代入差分方程使方程两边恒等，则称函数yx＝φ（x）为差分方程的解．如果差分方程的解中含有相互独立的任意常数的个数与该方程的阶相同，则称这个解为差分方程的通解；给任意常数以确定值的解称为特解．用以确定通解中任意常数的条件称为初始条件．

一阶差分方程的初始条件为：y0＝a0（a0为常数）；二阶差分方程的初始条件为：y0＝a0，y1＝a1（a0，a1为常数）；以此类推．

一阶常系数线性齐次差分方程的一般形式为

其中a≠0为常数．

下面介绍它的求解方法．

1）迭代法

设y0已知，将x＝0，1，2，…依次代入方程（1），得

yx＝Ca*．

2）特征根法

即

得λ＝a．称方程（2）为齐次方程（1）的特征方程，而λ＝a为特征方程的根（简称特征根）．于是y＝ax是齐次方程（1）的一个解，从而

y＝Cax（C为任意常数）

是齐次方程（1）的通解．

例4　求差分方程3yx＋1－2yx＝0的通解．

解　特征方程为

3λ－2＝0，

一阶常系数线性非齐次差分方程的一般形式为

其中a≠0为常数，f（x）为已知函数，且f（x）≠0．

定理　如果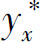是一阶常系数线性非齐次差分方程（3）的特解，Yx是对应齐次差分方程（1）的通解，则差分方程（3）的通解为

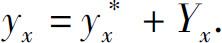
由定理可知，一阶常系数线性非齐次差分方程（3）的通解由它的一个特解与相应的齐次方程（1）的通解之和构成．由于相应齐次方程的通解的求法已经解决，因此只需讨论非齐次方程特解的求法．

下面仅就函数f（x）为几种特殊形式的函数时，采用待定系数法求非齐次方程（3）的特解．

1）f（x）＝Pm（x）

Pm（x）是m次多项式，此时方程（3）为

如果1－a≠0，即1不是特征方程的根，则方程变为

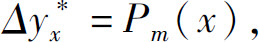
综上所述，有如下结论：

如果f（x）＝Pm（x），则一阶常系数线性非齐次差分方程（3）具有形如

的特解．其中Qm（x）是与Pm（x）同次的待定多项式，k按1不是特征方程根或是特征方程根依次取为0或1．

例5　求差分方程yx＋1－3yx＝－2的通解．

解　特征方程为

λ－3＝0，

解得λ＝3，故对应齐次方程的通解为

b－3b＝－2即b＝1，

yx＝1＋C·3x．

例6　求差分方程yx＋1－yx＝3x2的通解．

解　对应齐次方程

yx＋1－yx＝0

的通解为Yx＝C．由于1是特征方程的根，于是令

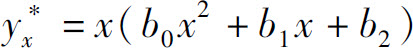
代入原方程，得

比较两边同次幂的系数，得

所以原方程的通解为

2）f（x）＝ρxPm（x）

这里ρ≠0为常数．当ρ＝1时，即为f（x）＝Pm（x）的情形，因此只需讨论ρ≠1的情形．

作变换yx＝ρxzx，代入方程（3），得

消去ρx，得

由前面的讨论知，可设它的特解

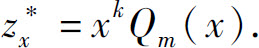
因此，有如下结论：

如果f（x）＝ρxPm（x），则一阶常系数线性非齐次差分方程（3）具有形如

的特解．其中Qm（x）是与Pm（x）同次的待定多项式，k按ρ不是特征方程的根或是特征方程的根依次取为0或1．

注：上述结论同样适用于ρ＝1，即f（x）＝Pm（x）的情形．

例7　求差分方程yx＋1－3yx＝7·2x的通解．

解　对应其齐次方程的通解为

Yx＝C·3x．

从而得b＝－7．因此，原方程的通解为

1．求下列函数的一阶和二阶差分：

（1）yx＝x（x－1）（x－2）…（x－n）；

（2）yx＝32x．

2．求下列一阶常系数线性齐次差分方程的通解或特解：

（1）2yx＋1－3y0＝0；

（2）yx＋yx－1＝0；

（3）yx＋1＋5yx＝0，且y0＝3．

3．求下列一阶常系数线性差分方程的通解或特解：

（1）Δyx－4yx＝3；

（2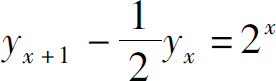），且y0＝2；

（3）yt＋1＋4yt＝2t2＋t－1．