黄金分割数

分已知线段为两部分，使其中一部分是全线段与另一部分的比例中项，这就是在中学几何课本中提到的黄金分割问题。若C为线段AB的满足条件的分点，则可求得0.618AB。这个分割在课本上被称作黄金分割，我们有时也可说是将线段分成中末比、中外比或外内比。若记，则φ（≈0.618）被称为黄金比或黄金分割数。黄金分割、黄金分割数都被冠以“黄金”二字，说明了它们的重要性与应用上的广泛性，同时也为它们平添了几分神秘的色彩。下面先让我们寻踪探迹说说它的名称由来。

最早对中末比有所了解的大约是毕达哥拉斯学派。他们对某一个几何图形怀有一种特殊的敬意，这个图形不仅具有很高的审美价值而且从磨砺智力的角度来看也是非常有意思的。这个图形他们称之为五星图，是在正五边形的基础上作成的。这个图形有着许多奥秘。比如，这个图形中的每一条线段，都跟比它稍短的那条线段形成黄金分割比。对该学派而言，五星图是一个神圣的符号，他们曾把“五角星”作为他们的徽章与联络标记，称之为“健康”。由于正五边形、正十边形和五角星形的作图与中末比是密切联系的。所以，如果相信毕达哥拉斯学派熟知正五边形与五角星的作图，那么可以推知他们已掌握了黄金比。如果这种推测成立，那么可以说黄金数和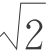一样，很早就被人们发现了。根据一些数学史家的看法，黄金数是最早发现的无理数。他们认为毕达哥拉斯学派可能用一种几何方法证明了：五星图的边和对角线是不可公度的，即黄金分割比值不是一个有理数。不过，即便黄金数放弃这一优先权，它还是获得了比更大的名气。

古希腊著名的数学家欧多克索斯对中末比做过系统的研究，他在深入探究五角星性质时，曾惊叹道：“中末比到底在这儿出现了！”对中末比的严格论述最早记载在欧几里得的《几何原本》中，在该书第四卷记述了用黄金分割作正五边形、正十边形的问题。到中世纪以后，中末比被披上更神秘的外衣，渐渐笼上了一层神秘的色彩。

文艺复兴时期，中末比问题引起了人们广泛的注意。1509年，帕乔里出版《神圣的比例》一书。书中系统介绍了古希腊中外比，并称其为神圣比例。他认为世间一切事物都须服从这一神圣比例的法则。达芬奇也认为“美感完全建立在各部分之间神圣的比例关系上。”开普勒写道：“毕达哥拉斯定理和中末比是几何中的双宝，前者好比黄金，后者堪称珠玉。”他是把黄金之喻给了毕达哥拉斯定理，而用珠玉来形容了中末比。最早正式在书中使用黄金分割这个名称的是欧姆（以欧姆定律闻名的G．S．欧姆之弟）。在1835年出版的第二版《纯粹初等数学》一书中，他首次使用了这一名称。到19世纪以后，这一名称才逐渐通行起来，成为现在人们所熟知的名称。

黄金分割数φ作为一个奇特的数，可以用许多有趣式子来表示。

如：由方程x2＋x－1＝0，可知，对其进行无穷多次迭代，则有：

利用上述方程，还可得到：同样进行无穷多次迭代，则有：

这是一个无限连分数，并且所有的元素都是1，形式极其漂亮。利用前面我们已经提到过的连分数理论，不难求得它的各个渐近分数分别为：

1／1，1／2，2／3，3／5，5／8，8／13，13／21……

我们还可以利用加成法来求一下它的近似分数。取1／2，2／3为母近似分数，利用加成法，可得到其一系列近似分数：

1／2，2／3，3／5，5／8，8／13，13／21……

它们恰巧与用连分数法求得的结果相同。

这一串渐近分数的分子、分母依次都是1，1，2，3，5，8，13，21……这一串数在数学上有一个专门名称，叫做斐波那契数列。因为这一奇妙的数列是由我们在本书中已经多次提到过的斐波那契这位中世纪著名学者，在他的《算盘书》一书修订本中提出的一道有趣的“兔子生殖问题”而引出的。这个有趣的问题是这样的：某人有一对兔子饲养在围墙中，如果它们每个月生一对兔子，且新生的兔子在第二个月后也是第个月生一对兔子。问一年后，围墙中共有多少对兔子。斐波那契在书中给出了分析，并提出，每个月的兔子总数可由前两个月的兔子数相加而得。这样，从一对兔子开始，随后几个月内兔子数分别为：

1，2，3，5，8，13，21，34，55，89，144，……

规律恰好是：从第三项开始每一项是前两项之和。这一问题因新颖巧妙，引起人们的广泛兴趣，许多人对此进行了研究。

斐波那契数列具有很多性质，它是如此有名，以致于1963年，美国创刊了一本专门研究它的杂志，被称为《斐波那契季刊》。

实际上，黄金数最引人注目的就是它与斐波那契数列的关系。两者会有什么关系呢？

让我们计算一下斐波那契数列中每前一项与后一项之比，就会发现这个比值竟与黄金分割数φ越来越接近，完全可以作为φ的一阶、二阶……N阶近似。多么奇妙啊！其实可以证明这些比值正是以φ作为它们的极限。

中末比与斐波那契数列的这种内在联系，为它大添光彩，也使它具有了一种特殊的神秘感与迷人的魅力，使后来的许多数学家为之倾倒。由于中末比具有各种独特的性质，随着它的影响越来越大，也就有了越来越多的关于它的传说。这些传说虚虚实实，令人扑朔迷离难辨真伪，但却一直为人们所津津乐道，广为流传。

有人研究得出黄金分割是植物形态的一个结构原则。如花的发育与黄金数有着极为密切的联系。百合花有3朵花瓣，毛莨有5朵花瓣，金盏花有13朵，翠菊有21朵，大多数雏菊有34朵、55朵或89朵花瓣。这些数字都是斐波那契数列中的数，因而也就与黄金数联在了一块。事实上，植物中出现的数字，不仅是花瓣的数字，包括植物的所有主要特征，即叶、花瓣、萼片、小花或其他诸如此类的生成都与黄金数有关。对于植物的生长是如何产生斐波那契数的，已经有许多人提出了各种不同的答案。

有人认为这一结构原则同样适用于人，即人的身体结构与黄金分割律有着十分密切的关系。对于人体来说，优美的身段可以通过躯干与身高的比体现出来，这个长度与身高的比值愈接近黄金分割数0.618时，就愈会给人一种美的感觉。或者说，人体自身美，即人体最优美的身段遵循着黄金分割比。据说著名的爱神维纳斯与女神雅典纳的雕像下身与全身之比近于φ。据说芭蕾舞艺术的魅力也离不开。芭蕾演员起舞时踮起脚尖，是为了展现符合φ的身段比例的最优美的艺术形象。有人还将女孩子爱穿高跟鞋的奥秘与黄金分割联系在一起。我们可以给出简单的解释：当人的躯干（肚脐到脚底的长度）与身高比为0.618时，能获得最佳美感，但可惜的是一般人的这一比值都低于0.618这个数值，大约只有0.58～0.60，而穿上高跟鞋就可以增加、改善这一比值，使得躯干与身高的比值更接近黄金分割的标准，从而产生美的效应。比如，某女孩的身高为160cm，她的原本躯干与身高比为0.60，那么当这位女孩穿上高度为4cm的高跟鞋时，其躯干与身高的比值将被提高到0.61左右；当其高跟鞋高度为7.5cm时，可以使得这一比值恰好等于0.618，从而获到最佳美感了！如此说来，女孩们相信穿高跟鞋使她们觉得更美倒是有数学根据的了。

世界上许多著名建筑广泛采用这一比例，给人以舒适的美感。如古希腊的巴特农神庙严整的大理石柱廊，就是根据黄金分割律的原则分割整个神庙的。这座建造于公元前5世纪的神殿的宽与高之比恰恰符合中外比，使这座神庙成为人们心目中威力、繁荣和美德的最高象征。

文艺复兴时期，黄金比在绘画、雕塑方面得到了多方面的应用，画家、雕塑家都希望从数学比例上解决最完美的形体，它的各部分的相互关系问题，以此作为科学的艺术理论用来指导艺术创造，来体现理想事物的完美结构。著名画家达芬奇在《论绘画》一书中就相信：“美感完全建立在各部分之间神圣的比例关系上，各特征必须同时作用，才能产生使观众如醉如痴的和谐比例。”达芬奇广泛研究过人类身体的各种比例。他对人体详细研究，在为帕乔里的《神圣的比例》一书所作的图解中，标明了黄金分割的应用。它还出现在未完成的作品《圣徒杰罗姆》中。此画约作于公元1483年，在作品中，圣徒杰罗姆的像完全位于画上附加的黄金矩形内，人们认为这应当不是偶然的巧合，而是他有目的地使画像与黄金分割相一致，因为在他的著作和思路中，处处表现出对数学应用的强烈兴趣。在这一时期，艺术家们自觉地被黄金分割的魅力所诱惑而使数学研究与艺术创作紧密地结合起来，并对后来形式美学与实验美学产生了巨大影响。

此外，我们知道现在包括我国在内的约40个国家的国旗上都有耐人寻味的五角星图案。为什么是五角而不是其他数目的角？据说就是因为五角星中蕴含着黄金比：正五角形的每条边恰好被与之相交的另外两边黄金分割。正是由于五角星多处暗含了φ这个美的密码，从而使这个图形赏心悦目。什么形状的矩形最美呢？建筑学家很早就研究过这个问题。因为盖房子要开窗口，窗子多数是矩形的，经过调查研究，大家认为，如果一个矩形，把它切掉一个正方形后，剩下的小矩形和原来的相似，看起来才是最美的，可以证明符合这一条件的最美的矩形的宽与长之比就是著名的黄金数，建筑师们常常把它作为门窗的比例。在中世纪欧洲就流行着依黄金分割法做的窗子最好看的说法，即黄金矩形（即两边的比等于φ的矩形）比用任何其他比值作边的矩形都要美观的说法。心理学家费希纳在1876年作过大规模的试验，他请300位生活背景、所受教育、职业、年龄都不同的人对面积相同，但长、宽不同的许多矩形，评选自认为是“最美”的。绝大多数人评选的最美矩形的宽与长之比在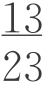～之间，有35%的人评选出比为的矩形，没有人选正方形。结果表明喜欢黄金矩形的人数占全体的三分之一，在各种矩形中得票最多。

诸如此类的说法还有很多。一句话：哪里有φ，哪里就有了美。黄金分割数成了宇宙的美神！黄金比除了具有美学的价值外，还在实际生活中有着极其广泛而又非常简单的应用。最广为人知的例子是它在优选法中的应用。

什么是优选法呢？在日常生产、生活和工程设计中，常常会面临这样一个问题：如何用最少的时间和步骤得出最佳的方案。比如说，要配制一种化学药剂，需要在其中加入10～50克的酒精，那么应该加多少呢，如果从加1克开始，然后是2克、3克……不断重复试验直到找到最佳克数，那么无疑是费时费力费料。优选法就是为了减少步骤而得到相同结果的迅捷方法。美国人基弗于1953年首先提出了优选学中的黄金分割法，使以黄金比为核心的0.618法成为人们所称道的一种很好的方法。这种方法在70年代曾被数学家华罗庚在全国大力宣传和推广，产生了巨大的经济效益。

还是举一个例子来说明其步骤：假若配制一种药剂需要加入1000～2000克的酒精，应该如何尝试求出最佳值呢？首先可以找一张大纸条，上面均匀地标好从1000～2000的数值，然后取其黄金分割点1618，划上一条线，再把纸条从正中央对折，在1618的线的正下方对应的点1382上也划一条竖线，相当于求出另外一个方向上的黄金分割点，然后取这两个值进行比较，看哪个更接近所需要结果，倘若1618的结果比较好，就把纸条从1382处剪去，剩下的点1618仍是黄金分割点，然后再对折，再划线，再比较，再剪去不需要的线段，这样很快就可以把范围缩得很小，而得到最佳值。

优选法中还有一种实质上与0.618法完全相同的方法叫分数法。这一方法是利用G的一串渐近分数，通过有限次数的试验，得到要求的结果，在实际中同样有着广泛应用。例如某种试验由于条件限制，只能做两次，这时可以把试验范围三等分，第一次试验取2／3处所代表的数值，然后仍旧利用“后一点”公式，得到第二次试验点。如果要求做三次试验就得出结果，那么可以把试验范围五等分，第一次试验取在3／5处。要求做四次试验，可以把试验范围八等分，第一次试验取在5／8处……

黄金分割在优选法中的运用又一次体现出数学发展的一个规律。它表明研究和发展数学理论是十分重要的。纯理论的发展对实践的作用也许不是直接的，但它所提示的自然规律必将指导人们的社会实践。斐波那契当年提出兔子问题，绝不会想到它有那么大的用处，而欧多克索斯研究中末比，更不可能知道他为优选法开辟了道路。数学理论往往是“前人种树，后人乘凉”，仅仅因为某种数学理论在应用上不能“立竿见影”，就轻率地加以否定，是缺乏远见的。