从贾宪三角到正负开方术

我们在上一节着重介绍了《九章算术》中的开平方和开立方的程序，并简单提到了刘徽、祖冲之、王孝通的工作。在这些工作之后，要在方程数值求解方面取得新进展需要面对两方面大的挑战。其一，开平方与开立方的方法都具有几何意义，而当方程的次数达到四次或四次以上时，依赖于几何的道路被堵塞了。其二，如何处理负系数。

在中国古代打开通道，把开方术推广到三次以上方程及负系数的突破都是在宋代完成的。这一工作由贾宪开创，刘益做出重要补充，并在秦九韶手中得以完成。在本节中，我们将简要介绍一下这三位数学家对此的贡献。

贾宪（约11世纪），北宋数学家。生平籍贯不详，活动在11世纪上半叶。他是数学家、天文学家楚衍的弟子，曾在朝廷里任“左班殿直”的低级武职小官。撰有《黄帝九章算经细草》9卷（约1050年）、《算法斅古集》2卷。两书都已失传。幸运的是，《黄帝九章算经细草》一书因被200多年后南宋数学家杨辉摘录进《详解九章算法》（1261），其大部分内容（约三分之二）得以保存至今。正是在这幸存的部分著作中，后人得以了解贾宪在高次方程数值求解方面作出的重要贡献。

在贾宪的数学成果中最著名的是“贾宪三角”和解高次方程的“增乘开方法”。所谓贾宪三角是如下所示由数字排列成的一个三角形图表。

用现在我们所熟悉的方式理解这张图表，它实际上给出的是指数n=0，1，2，3，4，5，6时，（a+b）n展开式各项系数的排列表。比如，第三行表示（a+b）2=a2+2ab+b2中的系数；最后一行“五乘”表示（a+b）6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6中的系数。这样的图表在西方最早可上溯到13世纪。再往后，我们第一章介绍过的塔塔里亚也曾发现这一数表。1527年，德国一本数学书的封面上又给出了这一数字三角。不过，这些都未能广泛流传。1654年，法国著名数学家帕斯卡（1623～1662）在所著的书中再次给出这一数表，并第一个正式指出这个数字三角是二项展开式的系数表，自此这一数表被流传开来。因此西方数学史上把这张数表称为“帕斯卡三角”。在国内，这一图表因为记载于杨辉的著作中，因此曾被称为“杨辉三角”，但杨辉在引用了这幅图后特意说明：“开方作法本源，出《释锁算书》，贾宪用此术。”因此，过去我国数学界把这幅图称为“杨辉三角”，实际上是不妥的，更恰当的称呼应是“贾宪三角”。可以看到，在时间上，贾宪比国外更早地提出了这一数表，因此我们完全有理由把这项由中国人最先发现的数学成果称为“贾宪三角”而载入史册。近年来，国外也逐渐承认这项成果属于中国，有些数学史书上开始称它为“中国三角”（Chinese triangle）了。

对贾宪本人来说，这张表不仅仅是（甚至也许在他的本意中没有打算）给出二项式系数，真正重要的是，它提供了解决开方问题的纲。为理解这一点，我们需要先对上图中出现的数字之外的文字做些说明。

贾宪将左右斜线上的数字1分别称为“积数”和“隅算”，将这两行斜线数字中藏的数字称为“廉”，开几次方，就用相应行的廉；第三行为“二”是开平方的廉；第四行“三、三”是开三次方的廉；第五行“四、六、四”是开四次方的廉，等等。“积”、“隅”、“廉”都是沿用中国古代开方术语。

“左袤乃积数”指左边由上而下的那一行数字“一、一……”是二项展开式中常数项系数；“右袤乃隅算”指右边由上而下的“一、一……”是展开式中最高次项系数；“中藏者皆廉”：中间那些数是对应各次项的系数；“以廉乘商方，命实而除之”：开方或解方程时用所得的商去乘各次项系数，再从实中减去（指开方各个步骤）。

我们举几个简单的例子体会一下如何用这种方法开方：求x3=1728的正根。

解：由1728为四位数，可知所求x必为二位数，设x=ab=10a+b，则有

（10a+b）3=1728，根据贾宪三角给出的二项式系数，有

（10a）3+3（10a）2b+3（10a）b2+b3=1728

估第一位商，由103<（10a）3<203，易知应取a=1。于是有

估第二位商，易知应取b=2，728-（300×2+30×22+23）=0

因为恰好余数为0，因此所求的x=12。

再看一个更复杂的例子（来自《九章算术》少广章第19题）：求x3=1860867的正根。

解：首先由1860867为七位数，可知所求x必为三位数，设x=abc=100a+10b+c，则有（100a+10b+c）3=1860867，根据贾宪三角给出的二项式系数，

（100a）3+3·100a（10b+c）2+3·（100a）2（10b+c）+（10b+c）3=1860867

估第一位商，由1003<1860867<（200）3，易知应取a=1。于是有

300（10b+c）2+3·104（10b+c）+（10b+c）3=1860867-1000000=860867，

由3·105·2<860867<3·105·3，可估第二位商b=2，于是所求x=[12c]，x3=（120+c）3=1860867，按二项式展开并整理可以得到

由43200·3<132867<43200·4，可估第三位商c=3，于是有

132867-（43200·3+360·32+33）=0

因为恰好余数为0，因此所求的x=123。

贾宪提出的释锁开方法显然可以应用到更高次方。我们举一个来自杨辉《详解九章算法》的例子：求x4=1336336的正根。

解：由1336336为7位数，可知所求x必为二位数，设x=ab=10a+b，则有

（10a+b）4=1336336，根据贾宪三角给出的二项式系数，有

（10a）4+4（10a）3b+6（10a）2b2+4（10a）b3+b4=1336336

由34·104<1336336<44·104，可估第一位商a=3。于是有

4（30）3b+6（30）2b2+4（30）b3+b4=1336336-（30）4=526336

由4（30）3·4<526336<4（30）3·5，可估第二位商b=4，于是有

526336-4（30）3·4-6（30）2·42-4（30）·43-44=0

因为恰好余数为0，因此所求的x=34。

显然，这样的思路可以推广到开五次、六次方。又因为贾宪的图表还蕴含着图中数字的产生规律。这种规律，用我们熟悉的方式可以表述为：两条斜边上都是数字1，其他的数都等于它肩上的两个数相加。但贾宪发现的规律略有不同，对此我们在下面将做介绍。不管如何，我们清楚的是，只要找到造表的规律，贾宪三角形可以写到任意层，换句话说，按照这个图表可以得到任意正整数次幂的二项展开式。于是，我们看到，只要借助贾宪三角形——解决开方问题的纲——就可以得到二项式展开的系数，进而我们就可以求解任意形如xn=A的高次方程。这种利用贾宪三角中的数字进行开方的方法被贾宪本人称为“立成释锁法”。其中释锁形象地比喻开方像打开一把锁；“立成”是指唐代以后天文学为计算各种天文数据立出的表格，此处喻“立等可取”。因此，立成释锁法就是指借助“贾宪三角”这一数表进行开方的方法。也正是由于这种用途，所以贾宪三角被称为“开方作法本源图”。因此，贾宪三角的提出，表明贾宪已经把开方问题推广到高次方。

在贾宪之前，从汉代一直到唐代的1000多年时间里，中国古代数学家只能进行正数的开平方和开立方运算，对于四次方以上的高次幂开方没有什么好的方法。贾宪“开方作法本源图”的出现，标志着中国古代实现了四次以至于更高次的开方，这在认识上是一个飞跃，在中国最早实现这个重大突破与飞跃的正是贾宪。

除此外，贾宪还以释锁开方为过渡和基础，进而创造了一种更为简捷的开高次方根的方法：增乘开方法。

为了理解贾宪的增乘开方法，我们首先来看一看他是怎样获得“开方作法本源图”中的各廉数的。他在“增乘方求廉法草”中给出的求贾宪三角第七行各数的方法相当于如下程序：将隅算1自下而上增入前位，直到首位为止，得第一位数字（上廉）；求其他各位数字，自下而上重复刚才的程序，每次低一位为止。

这是一种随乘随加的过程，所以叫“增乘法”。这种求廉的方法也就称为“增乘方求廉法”，显然，利用这种构造方法，可以把数表继续往下造。更重要的是，贾宪进而发现，这种增乘法不仅可以用来求“开方作法本源图”中的各廉，而且可以被推广用来直接开方，由此他创造了一种崭新的开方算法：增乘开方法。下面我们以求解x3=39304的正根为例，说明一下这种方法。为了与上面求“开方作法本源图”中各廉的过程相对照，我们采用一种比较易理解的方式做介绍。

贾宪的算法的第一步仍然是做缩根变换，由于39304为5位数，其开三次方后结果应为2位数，因此可令x=10x1，于是得变换后的方程为，议得首商为3。第二步是做减变换，令x1=3+x2。设方程变换为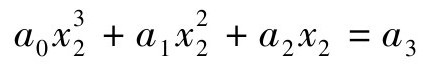：，其中系数a0，a1，a2，a3（分别对应于下法、下廉、上廉、实）由下列增乘程序来确定：

即得到减根变换后的方程为：

第三步仍然是做扩根变换，令x2=10-1x3，可得到变换后的方程为：

议得次商为4，再做减根变换，重复以上增乘程序

由于常数项恰好被减尽，整个计算至此为止。我们得到原开方式的正根为34。显然，求解过程中的缩根、扩根、估根与以前的做法基本一致。最大的变化在于如何确定减根变换后所得方程的系数。正是这一关键而复杂的一步，贾宪最初是用立成释锁法完成的，而这里则使用了随乘随加的增乘开方法。两者异曲同工，但后者比前者更简便、整齐，且更具程序化。

比如说，在开四次方根时，若运用二项展开式（a+b）4=a4+4a3b+6a2b2+4ab3+b4，在估得第一位数a后，为了继续求得第二位数，要计算a4，4a3，6a2，4a，然后通过（a+b）4-a4=4a3b+6a2b2+4ab3+b4=（4a3+6a2b+4ab2+b3）b来估b的值。这一步骤所需要的运算量不小。而增乘开方法的优点在于，a4，4a3，6a2，4a都通过随乘随加的方法得到，这就减免了一些重复性的计算。需要开方的次数越高，商的位数越多，增乘开方法的这种优越性就越明显。

增乘开方法另一优越之处在于：以前的算法在估计b值时对如何获得b讲得不够明确，算法也欠规范。增乘开方法则提供了一个累乘累加（减）的机械化算法，漂亮地解决了确定除数b的问题。由于增乘开方法在这种开方法中所起的关键作用，人们通常又把上面结合估算，通过不断缩、减、扩根三道手续，及求减根方程的完整开方程序称为增乘开方法。

贾宪本人发明的增乘开方法有两种：增乘开平方和增乘开立方。由此他处理了xn=B（其中n≤4，B为正数）的特殊形式的方程。但这种崭新的非常有效和高度机械化的算法，显然可适用于开任意高次方，即求xn=B的正根。

于是到11世纪中期，随着贾宪工作的问世，《九章算术》中的开方法不仅被推广到开任意高次方，而且一下子有了利用“开方作法本源”的立成释锁法与“增乘开方法”两种实现这一点的方法。它们的问世，标志着中国开方术发展到了一个新的阶段。更重要的是，贾宪的这两项成就对整个宋元数学产生了重大的影响，他也因此成为宋元数学高潮的“启动者”。特别是被看做是他最重大数学创造与最重大贡献的增乘开方法，不久后即先经刘益后被南宋数学家秦九韶推广，发展出在中国数学史上大放光彩的任意高次方程的数值解法。

下面我们就先来简单看一下刘益的工作。

刘益，中山（今河北定县）人，身世不可考，大约生活于12世纪中叶。曾撰《议古根源》。原书已失传，幸亏南宋数学家杨辉在自己《田亩比类乘除捷法》一书中摘引了这书的部分内容，后人得以了解刘益的数学贡献。具体说就是，刘益通过自己创造的益积开方术与减从开方术成功求解了x2-12x=864，-x2+60x=864，-8x2+312x=6912等方程的正根。

在刘益之前，不论开带从平方法、开带从立方法，或增乘开方法，都要求首项系数为1，而刘益所解决的问题则突破了这一限制。更重要的一方面，在刘益之前，都要求方程的系数为正。在负系数方面，只有祖冲之可能做过一些研究，但其方法先是因为深奥未被理解，后来则失传了。所以在其后长时期内，对方程的研究仍停留于正系数的情形。直到刘益才重新突破了开方式系数皆为正数的限制，通过引入并解决负系数方程，把数值解方程从正系数推广到负系数。

以现代人的眼光看，能求解这些方程似乎没有什么。但在当时，刘益的结果却具有重大的创新。杨辉誉之“引用带纵开方、正负、损益之法，前古所未闻也。”“撰《议古根源》二百问，带从益隅开方，实冠前古”。

这之后，在高次方程的解法方面，南宋数学家秦九韶（后面会对他做更详细的介绍）集前人数值解方程知识之大成，特别是在贾宪和刘益研究基础之上，进一步发展出一套完整的利用增乘开方法解高次方程的程序，称为正负开方术，现又称秦九韶法，最终彻底解决了任意次实系数多项式方程正根数值解问题。

秦九韶求高次方程正根数值解的一般方法记录在其名著《数书九章》中，我们以此书卷5中的“尖田求积”问题为例，说明其解法的运算步骤。

“尖田求积”是一个实际问题，最后可化为求解一个四次方程，用现在的符号可表示为：-x4+763200x2-40642560000=0。

秦九韶当时使用的仍是算筹。于是上面的方程用算筹布置可得到如下左图。最下一行“隅”表示最高项的系数，此处即x4的系数，“益”表示此系数为负。“下廉”表示次高项的系数，此处指x3的系数，“虚”表示该项系数为零。“上廉”表示x2系数，“从”表示此项为正。“方”表示一次项x的系数，“虚”表示此项系数为0。“实”表示常数项。在秦九韶的规定中，“常为负”，即“实”总规定为负数。“商”即所求方程的根，九韶规定“商常为正”，即根永远是正的。

更一般地，我们现在所熟悉的形如的高次方程在筹算中可布置算筹如下右图所示。其中最高项系数称为“隅”，一次项系数称为“方”，常数项称为“实”，其余各项称“廉”。按次数由低到高的顺序依次为上廉、二廉、……下廉。

在布置好算筹后，秦九韶又用了20个图式详细记录了自己的演算过程。为简洁起见，我们下面把他的图式合并为7个图，并附以说明。

在图（1）中，首先对各系数做了移位：其中“虚方”向左移了二位；“上廉”向左移四位，下廉向左移了六位，隅向左移了八位。从方程变换角度而言，这一步相当于对原方程做了x=100x1的扩根变换，得到。在做了这一步后，就可以先估得“商”的首位数字（在本例中是百位数字）为8。

在图（2）中，用商8乘益隅得负下廉-800000000；用8乘负下廉，并与原有的上廉相加，得上廉1232000000；用8乘上廉得方9856000000；用8乘方得“正积”78848000000，并与原来的负实相加，得正实38205440000。

图（1）

图（2）

在图（3）中，用8乘益隅，并与原来的下廉相加得下廉-1600000000；用8乘此下廉，并与原有的上廉相加得上廉-11568000000；用8乘上廉并与原有的方相加，得方-82688000000。

在图（4）中，用8乘益隅，并与原来的下廉相加得下廉-2400000000；用8乘此下廉，并与原上廉相加，得上廉-30768000000；用8乘上廉并与原有的方相加，得方-82688000000。

图（3）

图（4）

在图（5）中，用8乘益隅，并与原下廉相加得下廉-3200000000。

图（5）

由图（2）到图（5），是在求得了第一位得数8之后，为了继续求第二位得数所做的准备工作。从方程变换的角度而言，就是做了减根变换x2=x1-8，并得到了新方程：

当然，这一结果我们也可以通过直接把x1=x2+8代入

，然后借助于二项式展开得到。但不难想象其运算量之大。而秦九韶如上所使用的“增乘开方法”却按照自下而上随乘随加的方式，大大简化了计算。这正是增乘开方法的优越性之所在。

下面在此基础上确定第二位得数。

在图（6）中，先对各系数做了移位：其中“方”退一位即向右移了一位；“上廉”向右移了二位，下廉向右移了三位，隅向右移了四位。从方程变换角度而言，这一步相当于对原方程做了x3=10x2的扩根变换，得到

在做了这一步后，就可以议得（对此秦九韶提出可以用方除实的试除法）“商”的第二位数字（在本例中是十位数字）即次商为4。

在图（7）中，用次商4乘益隅，并与原来的下廉相加得-3240000；用4乘此下廉，并与原来的上廉相加得上廉-320640000；用4乘此上廉，与原来的方相加得-9551360000；用4乘方，并与原来的正实相加。此时恰好结果为0。于是操作结束，并得到840为方程的一个正根。从方程变换的角度而言，由于最后求得了x3=4，于是

图（6）

图（7）

总结秦九韶关于一般高次多项式方程的数值求解方法，我们看到其基本步骤是：首先缩根，使新方程的根的整数部分[x]是个位数，然后估计这个[x]；再做x-[x]减根变换，得到一个新方程；然后再次扩根（10倍），使这一新方程的整数部分是个位数，然后估出这个数，再减根……如此反复运算，直到余数为0。当所求根是无理数时，秦九韶使用刘徽求“微数”思想，用十进小数作无理根的近似值，并通过将同样程序一直进行下去的方式，求得所需精度的根的近似值。这在世界数学史上也是最早的。

事实上，这些基本步骤，正如我们上面已经介绍过的，在秦九韶之前大都已经存在，有的甚至可以远溯至《九章算术》。但就方程的次数而言，自《九章算术》至宋初，都局限在二次或三次。直到贾宪引入“贾宪三角”及“增乘开方法”之后，才突破了这一局限。但贾宪利用自己的方法只探讨了如x2=N, x3=N之类的方程，即纯开方问题，并没有进一步探讨含更多项的方程。就方程的系数而言，到贾宪为止都要求为正数。直到刘益才取消了以前对方程系数只允许为正的限制，也不再要求首项系数为1。

秦九韶正是在博采众家之所长的基础上把数值解方程的理论和技术又进一步发展，将增乘开方法推广到高次方程的一般情形，使自己的研究成为自秦汉以来中算开方术的集大成之作。

在其《数书九章》一书81个问题中，用方程来解的有21个，共列出了26个方程，其中二次方程20个，三次方程1个，四次方程4个，另外还有1个高达十次的方程如下：x10+15x8+72x6-864x4-11664x2-34992=0。而这些方程的系数既有正的，也有负的；既有整数，也有小数，在有理数范围内没有限制。

秦九韶用自己的“正负开方术”圆满地解决了这些方程的求解问题。在具体求解过程中，有些步骤他固守了中算的传统，如每次只求出根的一位数。为此不得不做缩根、扩根变换。但在关键的减根变换中，他吸收了贾宪的增乘开方法并将之应用于更广泛的情况以计算减根变换后新方程的系数，从而使自己的方法可以求解任何数字方程的正根。秦九韶本人对此有深入的认识。事实上，他书中特意构造的十次方程就是为了说明自己方法的普遍性。

另一点值得指出的是，秦九韶方法中“实常为正”的规定。显然，这一规定并不影响所研究方程的任意性。而之所以附加这一要求，是为了在增乘开方法的计算程序中彻底实现机械化的随乘随加。如果没有这一要求，在以试商由下而上累乘累加的过程中，要将所得结果从常数项中减去；而秦的程序由于规定了“实常为负”，整个运算便统一为加法。不久后，金朝数学家李冶就在《测圆海镜》（1248）中取消了常数项为正的限制。

秦九韶的工作，标志着中国传统数学开方术（从简单的开平方到以增乘开方法为主体的高次方程数值解法）已发展到十分完备的程度。这是中世纪数学的一项杰出成果，在世界数学史上亦占有崇高的地位。为了做比较，在详细介绍了秦九韶法后，我们再简单介绍一下现代数学中使用的霍纳法。

霍纳法借助的是现在所称的综合除法。我们从一个较简单的情况出发说明一下。

考虑x-b除a0x3+a1x2+a2x+a3所得的商和余式。直接做长除法或用待定系数法都可解决这一问题。我们这里不再做具体演算，只是把结果列出来。最后可求得

商的各项的系数和余式依次是：，。

仔细观察一下，会发现其中的规律：第一个系数是被除式中的首项的系数；第二个系数是被除式的第二个系数加上商的第一个系数与b的积；第三个系数是被除式的第三个系数加上商的第二个系数与b的积……

这一规则，我们可以借助于下面的式子来实现。

具体说就是：先把a0、a1、a2、……等系数摆放成一行。a 0直接落下；然后用a0乘以b，置于a1下面，两者求和得到a1+a0b；用a1+a0b乘以b，置于a 2下面，两者求和得到a2+（a1+a0b）b……

这种便捷的方法不仅适用于上面所举的情况，事实上，它可以用来方便地求出任意次多项式除以二项式的商及余式。这种方法就被称为综合除法。举一个例子。

求x3-4x2+6x+7除以x-1的商式及余式。

利用综合除法有：

于是，商式为x2-3x+3，余式为10。

下面，我们继续考虑这样的问题：

若x3-4x2+6x+7=A（x-1）3+B（x-1）2+C（x-1）+D，如何确定出系数A, B，C, D。显然，D就是x3-4x2+6x+7除以x-1所得的余式10，因此D=10。进而可以看到，（x3-4x2+6x+7）-D除以x-1所得的余式即为C，而（x3-4x2+6x+7）-D除以x-1恰好就是我们已经求得的x2-3x+3，即x2-3x+3=A（x-1）2+B（x-1）+C。因此为了确定C，只需x2-3x+3除以x-1求余式即可，而这同样可以通过综合除法完成。

因此，C=1。同样的道理，这里得到的商式x-2除以x-1所得的余式即为B。

用综合除法有：

于是B=-1，而A=1。

在做了这些铺垫性介绍后，我们可以考虑与我们的主题直接相关的问题了：若方程x3-4x2+6x+7=0做减根变换x1=x-1，求变换后的新方程。

一种非常直接的方法是把x=x1+1代入原方程展开化简。但这种方法当方程比较复杂时运算量非常大。我们现在考虑另一种方法。设得到的新方程为，即A（x-1）3+B（x-1）2+C（x-1）+D=0，剩下的只要确定各个系数即可。显然，这一问题等价于由x3-4x2+6x+7=A（x-1）3+B（x-1）2+C（x-1）+D确定系数A, B，C, D。而对此，我们已经提到可以借助于综合除法得到。为了节省篇幅，一般把上面多次运用综合除法的过程合并在一起。即有：

利用上面的结果，我们就有减根变换后的新方程为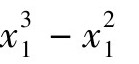：。这种利用综合除法求减根变换后新方程的简捷法正是霍纳法的关键。

于是，对秦九韶上面解决的方程可以用霍纳法解决如下：先估根800，然后对原方程做一个减根变换y=x-800。通过综合除法可求得变换后的新方程为-y4-3200y3-3076800y2-826880000y+38205440000=0。然后再估根40，再做减根变换z=y-40，余数为0。于是所求解为800+40=840。

为了做对照，我们把已介绍过的秦九韶的求解方法转换成如下形式：

两相对照，可以看到秦九韶的方法与霍纳法主要差别只在于，由于中算中所求的每一位商都是有关数位上的数，即每次得到的商都是一位数（在本例中第一位商取8，第二位商取4），所以具体操作要“进位”（相当于缩根）、“退位”（相当于扩根）。而霍纳法，则是在商里体现数位（在本例中第一个商取800，第二个商取40），这样就可以省掉“缩根”、“扩根”的步骤。而之所以有这种差别，主要原因在于中算的演算要借助于算筹。在筹算中，进位、退位操作并不复杂，而每次只得一位数的商却可以降低运算量。因此对使用笔算的现代人来说，霍纳法在操作上可能更显方便些，但对习惯于算筹的古代人来说也许秦九韶法的操作更显便捷。除此差别外，两者几乎完全一致。霍纳法于1819年由霍纳提出，比秦九韶晚572年，比贾宪晚了700多年。这正是中算的这一杰出成果值得书写的原因。

多项式方程数值解法在我国有悠久的历史，首先是在《九章算术》中提出了世界上最早的多位数开方程序，奠定了中国开方术历史的良好基础。其后，开方术经过刘徽、王孝通、贾宪、刘益、秦九韶等的不断改进、发展，最终创造出了求多项式方程数值解的秦九韶法。这一成就遥遥领先于世界各国，并对一些国家的数学发展产生了积极与重大的影响。

17世纪，随着《杨辉算法》（1378，宋代杨辉著）、《算学启蒙》（1299，元代朱世杰著）等中算著作陆续传入日本，日本数学家对中算数值解高次方程的方法有了一定程度的了解。日本著名数学家关孝和（后面将对他做更详细的介绍）在《杨辉算法》的启示下，独立发现了增乘开方法。在此基础上，关孝和又推陈出新，进一步发展了高次方程数值解法。在其专著《开方算法》中，关孝和详述多项式数值解的理论问题。其中许多出色工作令人出节称赏。比如他曾在研究正19边形中得到一个次数高达18次的方程：19R18-285R16+1254R14-2508R12-2717R10-1729R8+665R6-152R4+19R2-1=0。熟练应用正负开方法，关孝和得到精确度非常高的结果：R=3.03776691。考虑到这一方程次数之高、之复杂，以及当时计算工具的落后，就不能不为关孝和求高次方程数值解方面的深厚功底所折服。而且，在具体应用增乘开方法的过程中，关孝和做了一个改进：“先起于一个数，视开方各级而窥其位”。这使得其开方法较之中算家的开方法更具一般性。

在这方面的研究中，关孝和还提出了课商术与穷商术。穷商术，是把秦九韶求微数法与南北朝时期数学家张丘建求近似根的一种方法相结合以获得较高精度的方法，它兼有张、秦算法优点，同时可以获得根的好几位有效数字。课商术更是一种新创。课商中的“课”有试测的意思。课商是指，在应用增乘开方法时，从方程常数项的大小变化来调整所试测的商是太大还是太小。比如解方程2x3-11x2+24x-18=0。如下所示，先减根1，发现常数项由-18变为-3，没有变号。于是继续减根。在再次减根1之后，常数由-3变为2，变号了。于是加根。在加根0.5后，常数项恰为0，因此所求方程的根为1+1-0.5=1.5。中算中只有减根，关孝和推广为加根，填补了中算减根之不足，可谓青出于蓝。

在方程理论方面，关孝和也有许多创见。如他不仅承认负根，而且还对虚根有所认识。他把只有负根的方程称为“负商式”，把只有虚根的方程称之为“无商式”，他还研究了方程正、负根的个数问题，提出了方程的判别式并研究了正负根存在的条件。

在阿拉伯，15世纪伊斯兰著名数学家卡西（？～1436）的《算术之钥》（1427）是中世纪伊斯兰民族有关这方面数学文献中最完整之作。书中除介绍开平方、开立方外，还系统介绍了开任意次高次方程的方法，其方法从划分小节（即“超×等步之”）起，到求出根的各位数值之后进行减根变换，一直到对开方不尽的处理方式，与我国增乘开方法几乎完全相同。数学史家认为卡西的这些工作受到了中国数学的显著影响。

在欧洲，关于高次方程数值解法的探讨最早出现在13世纪。当时意大利数学家斐波那契在一次神圣罗马帝国宫廷应试中，给出了三次方程x3+2x2+10x=20的一个数值解x=1.3688081075，精确到小数点后9位数字。时人神乎其技，但因为他没有公开自己的解法，人们对他是如何求得这一结果的大惑不解。许多数学史家推测斐波那契使用的就是增乘开方法。如两卷本《数学史》的作者史密斯在卷2中说：“没有人知道这个结果是怎样获得的，但是这类数值方程的解法当时在中国已解决，并且那时东西方已有交往。从这些事实中，人们相信斐波那契是在旅游中学到的解法。”而比利时学者李倍始也认为，“如果斐波那契知道增乘开方法的话，那么非常可能他是从伊斯兰国家数学工作者那里学来的，而后者师承于先行者——中国学者。”

到19世纪，欧洲又重新独立得到了这一数值求解方法。先是在1804年，意大利数学家鲁菲尼（1765～1822）发现了一种逐步逼近法解数字系数高次方程。不久，英国中学老师霍纳（1786～1837）于1819年发表论文“连续近似解任何次数值方程的新方法”，并在伦敦皇家学会宣读。在论文中他举了六个例子，前面五例都是多项式方程。如问题一是求48228544的立方根；问题二是解x3-2x=5。霍纳在文章中对自己的方法做了一个详尽得近乎烦琐的分析，而且还强调其应用不仅限于代数方程，也可及于其他方程。霍纳提出的这一方法随后被广泛流传，西方数学史上称之为“霍纳法”（也称鲁菲尼—霍纳法）。数学家德·摩根曾对这一研究做出评价说“必使发明人因为发现了被前人忽略了的简单而普遍合适的算法而置身于重要发明家之列。”

正如我们已经介绍的，霍纳的方法与增乘开方法两者在原理上是完全相同的，只是霍纳法没有缩根、倍根变换。最早指出霍纳法与增乘开方法两者在原理上完全相同的是英国传教士伟烈亚力（1815～1887）。他于1847年来到中国。后经勤奋学习，很快掌握了汉语，并深入了解了中国的传统文化。1852年，他与中国数学家李善兰合作翻译了欧几里得《原本》后九卷。更令人惊异的是，在西学东传的同时，他还做了中学西播的反向传导。自1852年8月起，他陆续在《北华捷报》发表他研究中国传统数学的心得体会，题名“中国科学札记”。由于兼通中西数学，伟烈亚力得以对中西数学的相同与差异做出对比研究。在对秦九韶《数书九章》研读后，他把秦九韶的方法介绍到西方，并做出恰当评论：“此法在中土为古法，在西土为新法。”伟烈亚力还以秦九韶书中-x4+1534464x2-526727677600=0一题为例，详尽地阐述了秦九韶原著中的算法。然后他指出：“在这一运算过程中，读者立即觉察到了霍纳先生最初发表于1819年的‘解所有次方程的’著名定理……应该对霍纳的发明权提出质疑，对于欧洲朋友来说，发现来自天朝帝国的、有着十分合理机会获得优先权的竞争者，或许会是一件意想不到的事……”。作为比较，伟烈亚力还给出了同一方程的霍纳解法。

1910年，日本著名数学史家三上义夫（1875～1950）出版《中国和日本数学发展》，全面介绍了秦九韶的《数书九章》，其中包括以尖田求积题为例，用现代数学语言深入讲解了秦九韶的正负开方术。之后，英国科技史家李约瑟在《中国科学技术史》第三卷中，何丙郁在《科学家传记辞典》中又都对秦九韶包括正负开方术在内的工作做了介绍与评述。

1973年，比利时数学教授李倍始出版英文著作《13世纪中国数学》，这书是关于《数书九章》的研究专著。全书广征博引，详尽地介绍了秦九韶的全部工作。其中，他以很大篇幅全面论述了从贾宪、刘益、杨辉到秦九韶在数值解方程方面的成绩。从此再没有西方学者对秦九韶高次方程解法发表质疑。中国传统数学的这一杰出研究成果获得了世界公认。

在成书于1世纪下半叶的经典著作《九章算术》“少广章”中最早记载了开平方术和开立方术。用现代记号表述，开平方术相当于解方程x2=A，开立方术相当于解方程x3=A。在《九章算术》的开平方术中，实际上还包含了二次方程x2+bx=c的数值求解程序，被称为“开带从平方”。到唐代时，数学家王孝通在《缉古算经》中研究了“开带从立方”，书中他给出28个形如x3+px2+qx=c的正系数方程，并得出其正有理根。这表明，王孝通已掌握了求三次方程正根的数值解法。这些方法在宋元时代发展为一般高次方程的数值求解。先是在11世纪，宋代数学家贾宪创造出一种新的开方法——增乘开方法，通过随乘随加导出减根方程，逐步求出高次方程的正根。其后，12世纪北宋数学家刘益第一次突破方程系数为正的限制。在前人工作的基础上，南宋数学家秦九韶（1202～1261）总其大成，提出一套完整的逐步求出高次方程正根的程序“正负开方术”，用这种方法可以简便有效地求出形如的高次方程的正根。这种求高次方程正根的一般方法现被称为秦九韶法，它与英国数学家霍纳1819年创立的霍纳法基本上一致。秦九韶法的提出，表明中国古代数学已经能解决任意次方程的数值求正根问题。

从《九章算术》的开方术，中经刘徽、王孝通、贾宪、刘益，最后到秦九韶提出正负开方术，古代中国终于发展出十分完备的求高次方程正根的方法。而关于高次方程正根的研究又促进了古中国设未知数列方程的方法的诞生。

设未知数列方程，对具备初等数学知识的现代人来说可谓是轻车熟路，然而在古代完成这件事却困难得多。在中国直到宋代以前，数学家要列出一个方程，往往需要复杂的数学推导技巧和大量的文字说明。由于没有符号，只好借助于用文字叙述的形式来表达代数关系；由于没有代数方法，只能使用几何方法，方程的各项系数也因此要有相应的几何解释……这些都给列方程带来许多麻烦。对于较复杂的问题，列方程需要高度技巧，不是普通人能掌握的。

唐初王孝通的《缉古算经》被认为是深奥难懂的著作，主要原因就在于书中是通过复杂的文字叙述和烦琐的几何方法导出三次方程的。“昔唐王孝通撰《缉古算经》，于表中夸诩甚至，诚以创术之难也。”三次方程尚且如此，对于更高次的方程，其推导过程的困难就可想而知了。而且，高于三次的方程也难于找到几何解释。这使得列方程问题在王孝通之后直到宋之前漫长的时间里没有进展。

北宋数学家刘益最先迈出了一步。他熟练运用了一种推导方程的几何方法，称为演段术。演，推演之意，段指方程各项的图解，因为常用一段一段的面积表示，故简称段，也称片断或条段。演段实际上是用面积方法建立方程的过程。刘益用演段术解决了一些问题，但他还不懂得设未知数。后经蒋周等人的工作，演段术日趋完善。但这种方法的局限性是明显的，如它受限于几何解释，而且建立方程时没有固定程序等。随着高次方程数值解法的完善，创造一种简捷的列方程的方法成为迫切需要。

在这种背景下，大约在13世纪前后，一种关于设立未知数布列方程的一般方法——天元术在金元时期的北方应运而生了。最初的关于天元术的著作已经失传，创作者和年代难以详考。但诞生之初的天元术还不成熟，就像一棵小树一样。使之成长为一棵枝叶繁茂的大树的是金朝数学家李冶。

李冶（1192～1279）出生在金国统治下的大兴（今北京郊外）。他年轻时便对文史、数学均十分感兴趣，29岁考中金朝进士，被赞为“经为通儒，文为名家”。他曾在河南任知事。后蒙古人控制华北，李冶避难到山西，后隐居于河北元氏县，专门研究学问。他一生著作很多，但他最看重的是《测圆海镜》（1248）。他在弥留之际对儿子说：“吾平生著述，死后可尽燔去。独《测圆海镜》一书，虽九九小数，吾常精思致力焉，后世必有知者。庶可布广垂永乎？”李冶的遗愿得偿。作为现存最早的一部系统研究天元术的著作，也是天元术的代表作，《测圆海镜》的成书标志着天元术的成熟，并因此对后世产生了很大影响。元代大数学家朱世杰说：“以天元演之、明源活法，省功数倍。”清代阮元（1764～1849）说：“立天元者，自古算家之秘术，而《海镜》者，中土数学之宝书也。”它现在已被公认为中国数学史上颇有特色的名著之一。李冶数学方面的著作还有《益古演段》（1259），这是一本深入浅出介绍、普及天元术的杰作。《测圆海镜》《益古演段》两书的先后出版，大大促进了天元术的应用和发展。

所谓“天元术”，就是设未知数布列方程的一般方法。首先是“立天元一为某某”，相当于现在“设x为某某”。其中“天元一”就表示未知数（相当于现在的x），这个未知数具有纯代数意义，二次方不必代表面积，三次方也不必代表体积，常数项也可正可负。然后，根据问题给出的条件寻找两个相等的多项式；最后，再通过把这两个多项式相减，得到一个标准形式，即一端为零的一元高次方程。显然，用天元术列方程的方法，与现代代数中的列方程法已非常类似。在欧洲，直到16世纪才开始做到这一点。

“天元术”的出现，为数学家们列方程指出了一条简明易行的普遍方法和便于操作的具体程序，从而使中国古代的代数学又上了一个新的台阶。李冶之后不久，又先后出现了二元术、三元术，被最终在元代杰出数学家朱世杰手中发展出了宋元时期又一辉煌成就：四元术。

朱世杰（约1260～1320），元代数学家。字汉卿，号松庭，是燕山（今北京附近）人。作为一位平民数学家和数学教育家，他“以数学名家周游湖海二十余年矣，四方之来学者日众”，“周游四方，复游广陵，踵门而学者云集”。

由于出生在北方，他继承和发展了北方的数学成就。又因为曾长期游学，他又得以吸收当时南方的数学成果。由此，朱世杰成为中国宋元时期数学发展的总结性人物，他的工作成为中国以筹算为主要计算工具的古代数学发展的顶峰。

朱世杰的代表著作有《算学启蒙》（1299）和《四元玉鉴》（1303）。前者由浅入深，从整数的四则运算直至开高次方、天元术等，包括了当时已有的数学各方面内容，形成了一个较完备的体系，值得指出的是，书中在中国数学史上首次记述了正负数的乘除运算法则。作为一部较好的启蒙数学书，它曾流传海外，影响了朝鲜特别是日本数学的发展。与《算学启蒙》的通俗性相比，《四元玉鉴》则是朱世杰多年研究成果的结晶。它的问世成为中国宋元数学高峰的又一个标志，其中记录了朱世杰的众多数学成就，最突出的有“招差术”（即高次内插法）、“垛积术”（高阶等差数列求和）以及“四元术”（多元高次联立方程组与消元解法）等。

四元术是在天元术基础上逐渐发展而成的，它“寓方程（指线性方程组）于天元一术”，是中国古老的“方程术”与新产生的天元术的结合。作为天元术的发展与推广，四元术首先是指四元高次方程组列方程的方法。在四元术开头处总要有“立天元一为××，地元一为〇〇，人元一为△△，物元一为**”，相当于现代的“设x, y，z, u为××，〇〇，△△，**”。然后在此基础上建立方程组。进而，朱世杰还得到了多元（最多四元）高次方程组的求解方法。在这方面，朱世杰创造了一套完整的消未知数方法，可以将多元高次方程组依次消元，最后化成一元高次方程，对此可用增乘开方法求解，由此即可解决整个方程组的求解问题。四元消元法是四元术的核心，这种方法在世界上长期处于领先地位。在西方，直到1779年法国数学家贝祖（1730～1783）提出一般的高次方程组解法，才超过朱世杰。可以说，四元术不但是中国古代筹算代数学的最高成就，而且在13～14世纪之际的全世界也是最高的成就。

天元术与四元术的先后问世，还意味着中国传统数学发展到宋元时期时所出现的一个深刻的动向，即由“文词代数”阶段向代数符号化阶段的转变。早期的中国古代数学处于“文词代数”阶段，这在《九章算术》中有非常典型的体现。在这本中国传统数学经典著作中，所有的内容——问题、解以及求解方法——都只用文字和数，而不用数学符号表示，其中没有“等号”，没有表示未知量的x，也没有现在学习代数学时使用的任何其他的符号工具。但在天元术与四元术中，开始出现了用特定的汉字作为未知数符号并进而建立方程的系统努力。它们可看做是一种半符号代数，当然，这还只是一种很不完备的符号代数。事实上，正如我们已介绍的，直到16世纪，在法国数学家韦达等人较系统地引入了字母表示数及常用的数学符号后，完善的符号代数才逐渐建立起来。

古典代数学的中心课题是方程论，通过本章的介绍我们可以看到，我国古代在列方程和解方程方面都取得了杰出的成就。可以说，列方程和解方程的过程，曾形成了中国多项式方程发展史上两条齐头并进的涓涓之流。这两股泉流的渊源则是《九章算术》中展示的开方法。而至宋元时期，随着正负开方术、四元术的出现，标志着中国数学家已在立任意次多项式方程并求解方面达到了精熟的程度。这些中国数学最具代表性的贡献在世界数学史上也有着其独特的地位。