非均匀介质中的光线理论

13.3.1　非均匀介质中的光线理论——程函方程与光线微分方程

1）程函方程

运用光线理论研究光在折射率是位置函数（n（r）=n（x，y，z））的非均匀介质中的传播规律时，可以采用从亥姆霍兹方程导出的一种近似波动方程——程函方程来表示光线的轨迹。

根据电场矢量的亥姆霍兹方程▽²E+k²E=0，可以导出标量形式的亥姆霍兹方程▽2V+k²V=0，并在几何光学近似条件下（λ₀→0），导出如下的表征非均匀介质中光线轨迹的程函方程：

［▽φ（r）］²=n²（r）　　　　　　　　　　（13.38）

或将等式两端作开方变换得到

|▽φ（r）|=n（r）　　　　　　　　　　　　　　（13.39）

式中：r=r（x，y，z）——位置的矢量；

　　　φ（r）=φ（x，y，z）=nr——位相函数，也是光程函数，它是位置的实标量函数。

上述程函方程（13.39）的物理意义表示：非均匀介质中各点位相函数的梯度（即最大位相变化）▽φ（r）与该点的折射率n（r）成正比。换言之，介质中折射率的分布情况决定了各点位相函数的梯度。介质中的等位相面由φ（r）=φ（x，y，z）=ct的面决定，程函方程中▽φ的方向是与等位相面垂直的，它代表了光波传播即光射线的方向。由于各向同性渐变折射率介质中，等位相的波阵面是弯曲的，因而光线的轨迹也是弯曲的；作为特例，若为各向同性均匀折射率介质，则等位相波阵面为平面，因而光线轨迹为直线。

总之，程函方程定性地给出了非均匀介质中光传播轨迹为曲线的明确物理概念。

2）矢量形式的近轴光线微分方程

为了得到光线传播的具体轨迹，需要建立并求解光线微分方程。

根据位置矢量r和光程函数的概念，利用程函方程，可以导出如下以n（r）和r所表示的光线轨迹方程，即矢量形式的光线微分方程：

上式是一个以r为变量的二阶微分方程，其特点是以位置矢量r=r（s）（即r（s）矢量端点的轨迹）来描述光线轨迹（见图13.15）。上式的严格求解困难，为此需导出近轴条件下近似的近轴光线微分方程。

当光线轨迹相对于光纤轴线z轴的夹角很小时，即在近轴条件下，可取ds≈dz，且式（13.40）左端可取n（r）≈n₁（n₁为光纤轴线上的折射率），则代入式（13.40）可以得到

上式即为近轴光线微分方程，又称“近轴光线方程”。上式表明，只要给定了渐变折射率光纤中的具体折射率分布函数n（r），代入上式即可求出r=r（s）的光线轨迹。

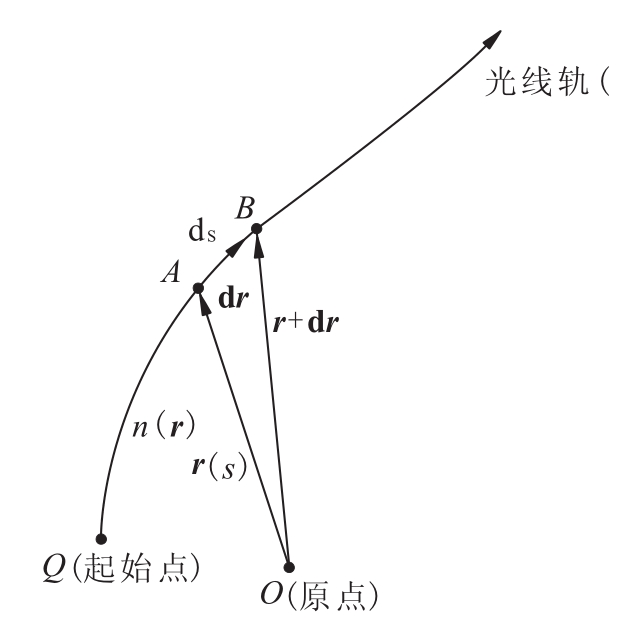
图13.15　非均匀介质中由位置矢量r=r（s）端点所描述的光线轨迹

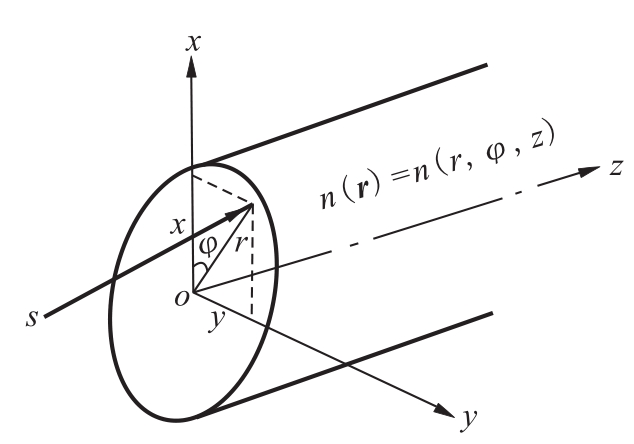
图13.16　圆柱坐标系表示形式

对非均匀介质，折射率是位置的函数，若以直角坐标系表示，应为n（r）=n（x，y，z）；但对轴对称圆柱介质光纤而言，则采用圆柱坐标系表示更为方便适用，即可表为n（r）=n（r，φ，z），如图13.16所示。式中r为光纤中半径变化参量，φ为相对于子午面的方位角参量，z为光纤轴向参量。然而介质折射率分布是（r，φ，z）三个参量的函数太复杂了，并不符合光纤介质中折射率分布的实际情况。实际上，人工可实现的渐变折射率光纤介质的折射率分布只是r的函数，即只随r而变化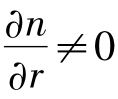；而与φ及z参量无关：在过光轴的任意子午面内其折射率分布规律均相同，因而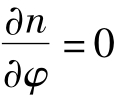；且在垂直于光纤轴线的任意截面内其折射率分布规率亦均一致，因而。

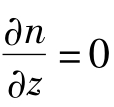这样，即可将研究空间光线的近轴矢量形式光线微分方程式（13.41）转化为研究子午面内的标量形式光线微分方程。即有

这样，若给定渐变折射率光纤的折射率随光纤半径的变化规律n（r），则可求解出光纤中光线运行的轨迹。