最近邻模型

20.4.1 最近邻模型

最近邻模型的关键思想在于一个特定输入点x的特性与x的邻居点是相似的。例如，如果我们要进行密度估计——也就是，对在x处的未知概率密度进行估计——那么我们可以简单地测量散布在x邻近区域内的点的密度。这听起来简单，直到我们意识到还需要确定“邻域”的确切含义。如果邻域范围过小，则有可能不包含任何数据点；如果过大，则可能会包含所有的数据点，造成各处的密度估计都相同。一种解决方案是定义邻域范围让它刚好包含k个点，其中k足够大，能保证进行一次有意义的估计。对于固定的k值，邻域范围的大小会发生变化——在数据稀疏的地方，邻域范围大，而在数据密集的地方，邻域范围小。图 20.12（a）显示了一个数据在两维平面上散布的例子。图 20.13 显示了对于这些数据的k-最近邻密度估计的结果，k分别取3，10和40。对于k = 3的情况，在任意点的密度估计仅仅基于3个邻居点，这种情况下可变程度是很高的。对于k = 10，这个估计提供了对真实密度的一个很好的重构，如图20.12（b）所示。对于k = 40，邻域范围过大，数据的结构几乎一起消失了。在实际应用中，对于大部分低维的数据集，使用一个介于5到10之间的k值会得到不错的结果。一个合适的k值也可以通过使用交叉验证进行选取。

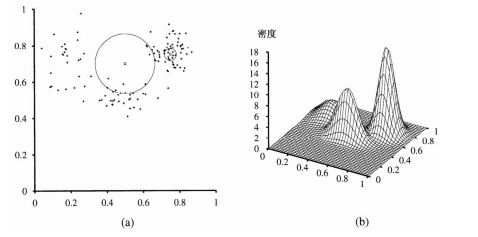
图20.12 （a）对图20.8（a）所示数据的一个128点的子样本，以及两个查询点和它们的10个最近邻。（b）一个生成这些数据的混合高斯分布的三维图示

为了确定一个查询点的最近邻，我们需要一个距离度量D(x1, x2)。图20.12中的二维例子使用了欧氏距离。当空间的每个维度度量的对象不同时，这种距离是不合适的——例如，高度和宽度——这是因为如果改变了某一维的尺度的话，最近邻集合就会随之改变。一种解决方法是对每一维的尺度进行标准化。为此，我们在整个数据集上度量每个特征的标准差，并将特征的值表示为对应特征的标准差的倍数。（这是马氏距离的一个特例，马氏距离还同时考虑了特征的协方差。）最后，对于离散的特征我们可以使用海明距离，它把D(x1, x2)定义为x1和x2之间不同特征的数目。

图 20.13 所示的密度估计定义了在输入空间上的联合分布。然而，和贝叶斯网络不同，一个基于实例的表示无法包含隐变量，这意味着我们不能像处理混合高斯模型时那样进行无监督聚类。倘若训练数据包含了目标特征值，在给定输入特征值x的情况下，我们还可以通过计算P(y|x) = P(y, x) / P(x)使用密度估计来预测目标值y。

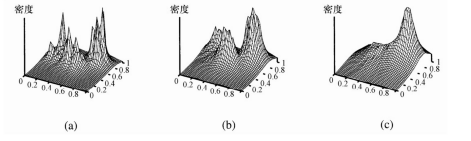
图20.13 使用k-最近邻的密度估计对图20.12（a）中的数据进行处理，k分别取3，10和40

将最近邻的思想用于直接的有监督学习也是可能的。给定一个测试样本的输入 x，输出 y = h(x)根据x的k最近邻的y值取得。在离散的情况下，我们可以通过简单多数投票得到一个简单的预测。在连续的情况下，我们可以求k个值的平均，或者进行局部的线性回归，用一个超平面拟合k个点，然后根据超平面预测x处的值。

k-最近邻学习算法很容易实现，几乎不需要调节，并且通常有很好的效果。对于一个新的学习问题这种算法应该是值得首先尝试的。然而，对于大数据集，我们需要一个有效的机制找到查询点x的最近邻——简单计算到每个点的距离会花太长的时间。人们提出了各种精巧的变形方法，通过对训练数据进行预处理而使得这个步骤更有效。不幸的是，大多数这类方法都无法随着空间的维数（即特征的数目）很好地进行扩展。

高维空间还摆出另外一个问题，也就是说这样的空间中最近邻通常会相距很远！考虑在d维单位超立方体中一个大小为N的数据集，假定超立方邻域的边长为b，体积为bd。（对于超球可以应用同样的参数，不过体积的计算公式要更复杂。）为了获得k个点，平均邻域范围必须覆盖整个体积（大小为1）的k / N部分。因此，bd= k / N，或b = (k / N)1/d。到目前为止一切顺利。现在令特征的数目d为100，k为10，而N为1 000 000。则我们有b≈0.89——也就是说，邻域范围几乎延伸到整个输入空间！这表明对于高维数据的情况，最近邻方法是不可信的。在低维空间中没有问题：当 d = 2时，我们得到b = 0.003。