最简单的数学模型

在数学中，再也没有比自然数更原始的对象了. 人类最早对自然数的理性认识，应是毕达哥拉斯学派. 毕达哥拉斯(Pythagoras，公元前572—前500)是古希腊著名的哲学家和数学家，以他为首建立了一个集政治、宗教、学术于一体的一个团体，后人称为毕达哥拉斯学派. 这个学派没有给后人留下什么著作，但据有关记载，这个学派的数学修养很高. 毕达哥拉斯学派认为，数学是创造和维持这个世界的神圣主宰者，认为万物包含数，数是万物的元质. 在这样的哲学思想下，他们对自然数作了多方面的、系统的和深入的考察. 具体说来有以下几项代表性的成果.

(1)发现了完全数和亲和数

他们把1视为正整数n的因数，但n却不是n的因数，并把一个整数的各个因数之和大于、小于或等于这个整数时，分别称为这个整数为过剩数、不足数和完全数. 如6=1+2+3，28=1+2+4+7+14就是两个完全数.

欧几里得给出了偶完全数的公式: N=2n-1(2n-1)，其中n＞1，且使2n-1为素数. 现在称2n-1形的素数为梅森素数(17世纪上半叶，一个叫梅森的法国人宣称，当n为素数，2n-1亦为素数，人们笃信无疑)，简记为Mn. 这个命题为后来者提供了研究空间，2000年来，研究者络绎不绝. 1903年，哥伦比亚数学家科尔(F.N.Cole)发现267-1不是素数，而是合数，第一个否定了M67为素数的断言，因为M67=193707721×761838257287. 人们才明白，Mn当n是合数时，Mn是合数，而当n是素数时，Mn却不一定是素数。但是数学界中寻找Mn的兴趣依然不减. 电子计算机出现以后，给人们验算和寻找梅森数带来了方便. 手算笔录时代仅找到12个梅森数，花了2000年的时间，它们是M1， M3，M5，M7，M13，M17，M19，M31，M61，M89，M107，M127. 从1952年到2004年短短50余年寻找到了29个梅森素数. 时至今日，人们已经发现了41个梅森素数.

2004年5月15日，美国国家海洋大气局顾问、数学爱好者乔希劳德利用一台装有2.4GHz奔腾处理器的个人计算机，找到了第41个梅森素数M24036583(即224036583-1)，它有7235733位数，是目前知道的最大素数.若普通书写每字占cm，这个数的长度可达三万六千多米(即相当36公里).

研究梅森素数有着十分重要的理论意义和实用价值: 它是发现已知最大素数的最有效途径; 它能促进数论的研究，也能促进计算数学、程序设计技术、网络计算技术及密码技术的发展; 还可用来测试计算机硬件运算是否正确. 科学家们认为，对于梅森素数的研究能力如何，在某种意义上标志着一个国家的科技水平.

毕达哥拉斯学派还发现了亲和数. 两个数是亲和的，如果每一个数是另一个数真因子之和，即如果a，b是两个整数，a的因数之和等于b，而b的因素之和等于a，则称a与b是一对亲和数. 例如220=1×22×5×11，其因数为1，2，5，11，4，10，20， 22，44，55，110等，其和为284. 而284=1×22×71，其因数为1，2，4，71，142等，其和恰为220. 因此，220与284即为亲和数. 它是毕达哥拉斯发现的第一对亲和数.

自此，寻找亲和数的工作持续不断地进行着. 1750年，瑞士著名数学家欧拉(L.Euler，1707—1783)一次就公布了60对亲和数. 数学家惊呼: “欧拉把一切亲和数都找完了.”可惜欧拉遗漏了稍大于(220，284)的一对亲和数: (1184，1210). 而这一对亲和数是意大利一位年仅16岁的青年巴格尼于1866年找到的.

阿拉伯数学家考拉(T.B.Korrah)给出了一个求亲和数的公式: x＞1，x∈N，a=3×2x-1，b=3×2x-1-1，c=9×22x-1时，若a，b，c皆为素数，则2xab与2xc是一对亲和数，显然，当x=2时，有220与284，就是第一对亲和数.

现在人们已经知道，10万以内的正整数有13对亲和数，而110万以内的正整数，总共有42对亲和数. 在数学家和数学爱好者的努力下，目前找到的亲和数已超过了1000对. 但是，亲和数是否有无穷多对? 它们分布有什么规律性? 尚无确定的答案，仍然是一个亟待探索的问题.

对于梅森素数的分布，中国数学家及语言学家周海中教授经过多年的研究，1992年给出了一个精确的表达式，被国际数学界命名为“周氏猜测”，是对梅森素数研究的重大突破.

(2)数与形的第一次结合

毕达哥拉斯学派在研究数时候，并不把数和几何上的点区分开来，他们按照点(或石子)的排列，研究“形数”，包括三角形数、正方形数、五边形数等等.

图1.1(a)所示称为“三角形数”，第n个三角形点的总数为

图1.1(b)所示称为“四角形数”，又称“四方数”，第n个四方形点的总数为

N4=1+3+5+…+(2n-1)=n2

图1.1(c)所示称为“五角形数”或“五边形数”，第n个五边形点的总数为

图1.1

继之为“六边形数”. 第n个六边形点的总数为

N6=1+5+9+…+(4n-3) =n(2n-1)

k角形点的总数为

以上这些结果显然是简单级数的求和. 我国数学从一开始，就对级数有浓厚的兴趣，例如古代一些数学名著《周髀算法》、《九章算术》、《孙子算经》、《张邱建算经》等就有等差、等比级数方面的问题和解法. 中世纪数学家如沈括、杨辉、朱世杰等，对级数的研究取得相当大的成就. 最为著名的有沈括的“隙积”和朱世杰的“垛积”.

宋代沈括讨论了累坛、层坛及酒家积罂等问题，对一个堆酒坛的问题作了深入的研究: 酒店里把酒坛层层堆积，底层排成一个矩形，以后每上一层，长和宽两边的坛子各少一个，这样堆成一个长方台形，问酒坛的总数是多少?

设底层长方台的相邻两边各放a和b个坛子，若一共堆了n层，则酒坛总数为

当a=b=n时，则所堆成的“垛”称为“正方垛”，这时酒坛总数是

元代朱世杰以先进的水平对高阶级数进行了研究，在他的《算学启蒙》和《四元玉鉴》两书中都占有一定的比例，创立了各种形式的计算公式，如“三角垛”、“撒星形垛”、“三角撒星形垛”、“三角撒星更落一形垛”等等. 以三角撒星形垛为例，其和是

由于微积分学的创立，级数研究和应用大大地扩展开来，在求级数和的某些方法上甚至成了18世纪数学思想的特征，并成为近代数学的一部分.

(3)毕达哥拉斯数组

数学史家曾在古巴比伦的泥板文书中发现了一张毕达哥拉斯约化三元数组表[2]，因此，毕达哥拉斯定理，实际上在毕达哥拉斯前1500年就发现了.

与“形数”的研究方法相同，毕达哥拉斯及其门人，所关心的是形成直角三角形三边的三元数组，他们发现2m，m2-1，m2+1，能代表一个直角三角形的三条边的长，称{2m，m2-1，m2+1}为勾股数(其中m是自然数)，但这组数并不能给出所有的勾股数组，如{7，24，25}.

欧几里得(Euclid of Alexandrio，约公元前300—前275)给出了一个公式: 若x，y是正整数，则有(x2+y2)2=(x2-y2)2+(2xy)2，且表达式a=x2-y2，b=2xy，c=x2+y2，将生成所有约化毕达哥拉斯三元数组. 可见，当时的巴比伦人已经知道上述公式的某种形式.

毕达哥拉斯学派在研究直角三角形时，发现了“直角三角形两直角边的平方和等于斜边的平方”这样一个定理. 在欢喜之余，宰牛百头，广设延宴，以示庆贺. 其实我国古代在周朝(前1100年)初年时，就发现了勾股定理.《周髀算经》有言“勾股各自乘而开方除之得弦”. 它并不囿于“勾三、股四、弦五”的特殊情形.

关于勾股定理的证明，现在世界上能找出400多种方法，对于勾股定理的研究，至今仍长盛不衰.

由勾股定理引出的猜想有很多，下面仅举几例.

(ⅰ)对称猜想

由a+b＞c和a2+b2=c2，根据对称性猜想a3+b3＜c3，成立吗?

(ⅱ)类比猜想

把边换成矩形或长方体，构成图1.2——面直角三角形和图1.3——体直角三角形.“面直角三角形”就是由矩形作成“直角边”和“斜边”，且两“直角边”的“夹角”是一个直二面角构成的空间图形; 而“体直角三角形”的各“边”是由长方体构成. 对于图1.2，记矩形ABCD的面积为S1，矩形BCEF的面积为S2，斜面矩形ADEF的面积为S; 对于图1.3，两“直角体”和“斜体”的体积分别记作V1、V2和V. 我们猜想，下面两组各三式是否正确?请你尝试证明或推翻.

对于长方体，若把长、宽、高以a、b、c记之，对角线记为d，我们知道有

a+b+c＞d，a2+b2+c2=d2

那么可否有 a3+b3+c3＜d2(1.7)呢?

图1.2

图1.3

如图1.4所示，直角四棱锥OABC中，OA⊥OB，OB⊥OC，OC⊥OA，三个侧面OAB，OBC，OCA的面积分别为S1，S2，S3，底面ABC的面积为S，类比于直角三角形勾股定理，是否有

图1.4

S1+S2+S3＞S(1.8)

呢? 如何判断.

还可进一步类比.

如果在直角三角形中，有c3＞a3+b3，c4＞a4+b4，推而广之，可否有

cn＞an+bn(n＞2，n∈N) (1.11)

同样，在“面直角三角形”和“体直角三角形”中，下述不等式

是否成立?类似地，在长方体和直角四棱锥中是否有

更一般地，我们猜想:

对于xi＞0，y＞0，y2=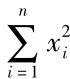，n≥2，m≥2，m，n∈N，

则

再进一步，我们猜想，对于xi＞0，y＞0，yp=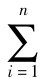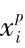，p＞2，n＞2， l ＜p ＜q，p、q∈N，则

上述猜想，都是正确的. 有兴趣的读者可参阅汪文贤著的《数学思维论》(浙江摄影出版社，2007年).

对于毕达哥拉斯数组，也可引发如下思索:

(1)任何一组毕达哥拉斯数，必有偶数(可用反证法证明).

(2)任一组毕达哥拉斯数，必有3的倍数，4的倍数或5的倍数.

由法国数学家费尔马(P. Fernat，1601—1665)源于毕达哥拉斯数组，提出的猜想是最有名的费尔马猜想，经过数学家们300多年的奋斗，1994年最终由英国数学家维尔斯(A.Wiles)证明.由费尔马猜想变成了费尔马大定理，这是20世纪数学上的伟大成就，是人类思维力量的一曲高歌.

(4)发现了无理数

毕达哥拉斯学派信奉宇宙间的一切现象，都能归结为整数或整数之比. 约公元前470年，学派成员希帕苏斯考虑边长为1的正方形的对角线长度. 根据勾股定理，对角线长度应满足l2=2.但什么样的数，它的平方是2呢?12=1，22=4，而12+12=2，显然l不是整数，它也不是分数，故l不是有理数. 后来亚里士多德(Aristotle，公元前384—前322，古希腊哲学家、思想家)证明:

若l=q/p，q/p是既约分数，则l2=(q/p)2=2，2p2=q2，于是q不是奇数. 设q=2k，k是自然数，进而4k2=2p2，2k2=p2，于是p不是奇数.设p=2r，r是自然数，从而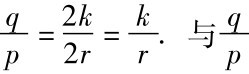是既约分数矛盾，所以l不是整数与分数.

毕达哥拉斯所谓“万物皆数”的数只是整数与分数，按照这个认识，单位正方形对角线的长就不是数! 毕达哥拉斯的绝对权威受到了严重的挑战. 传说当时学派全体成员正在爱琴海上泛舟集会，听希帕苏斯(Hisppasus)叙述有关发现，大伙不禁唏嘘，而毕达哥拉斯又不肯承认自己的观点有问题，当即决议禁止把此事张扬出去，泄密者死! 后来，希帕苏斯又把它透露出去了，按照教规，把他投入了大海. 希帕苏斯为自己的发明做出了牺牲.

事实上，这一发现是早期希腊人的重大数学成就之一，也是数学史上的一个里程碑. 然而，在当时却引起了一片哗然，因为希帕苏斯打破了毕氏学派的“信条”，而陷入了极大的矛盾之中.这就是数学史上“第一次数学危机”. 希帕苏斯关于无理数的发现，使得古希腊数学家完全否认运用算术和代数方法研究几何学的合法性，并无可奈何地接受了无理数的存在，而最终取得了合法的地位. 但关于它的理论，直到19世纪才被德国数学家戴德金(Dedekind Jnlins Wilheln Richard，1831—1916)严格地建立起来.

毕达哥拉斯学派研究“形数”，发现了数与几何图形的和谐性，并能作出五种正多面体的图形; 还研究了黄金分割、比例中项等，并利用简单整数比，创立了一套音乐和声理论，发现了数与音乐的关系. 总之，毕达哥拉斯学派凭心智来研讨数学问题，并把数学看成一门高尚的学术，自主地迈入了纯粹数学的门槛，并给予数学以演绎的特性.