随机挽回率下模型的扩展

三、随机挽回率下JLT模型的扩展

这一部分考虑模型在随机挽回率下的扩展,除非特别说明,市场结构与假设仍然同前面所述。假设信用等级状态集为:C={1,2,…,K,K+1,…,K+L}。其中S={1,2,…,K}为没有违约状态集,B=C-S为违约状态集,B中的每一信用等级与不同的挽回率一一对应,考虑一定义于B中的非负函数δ,对于i∈B,δ_i表示违约状态为i时的挽回率,通过假设S中的δ_i=1扩展到整个状态空间。假设δ_K+1≥δ_K+2≥…≥δ_K+L≥0,即δ_K+1表示最高的违约挽回率,δ_K+L表示最低的违约挽回率。因此违约时间可定义如下:

τ=inf{0≤t≤T|η(t)∈B}

这里,τ为关于信息集{F_t}的停时。

假设:

(1)如果公司在状态违约i∈B,债权人接受面值挽回率为δ_i,面值为1的有违约风险零息债券的到期支付为D(t,t)=1_{τ>t}+δ_η(τ)1_{τ≤t}。

(2)随机过程(η(t))_0≤t≤T为状态空间C中P概率测度下的稳定(时齐)(F_t)马尔可夫链,B中的每一信用等级为吸引的;且在风险中性概率测度Q下(η(t))_0≤t≤T为(F_t)马尔可夫链。

(3)在风险中性概率测度下,(r(t))_0≤t≤T和(η(t))_0≤t≤T相互独立。

类似于第二节,单期转移矩阵P=(p_i,j)_i,j∈C可表示为:

O为所有元素均为零的单期转移矩阵L×K矩阵,1为L维单位矩阵,矩阵R为违约状态,即p_i,j,i∈S,j∈B表示由状态i转移到违约状态j的概率。

同样假设市场为无完全套利,即存在与测度P等价的风险中性概率测度Q,在该风险中性概率Q下的转移矩阵表示为:

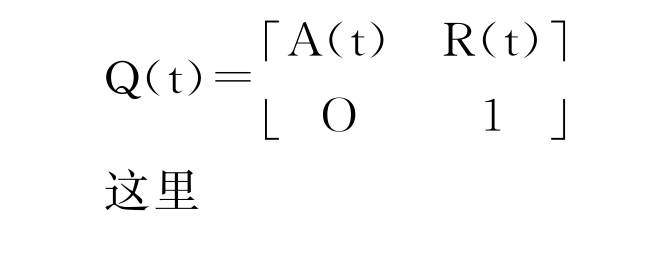
给定单期转移矩阵,通过下式计算从s时刻到t时刻(0≤s≤t≤T)的转移矩阵Q(s,t)=(q_i,j(s,t))_i,j∈C:

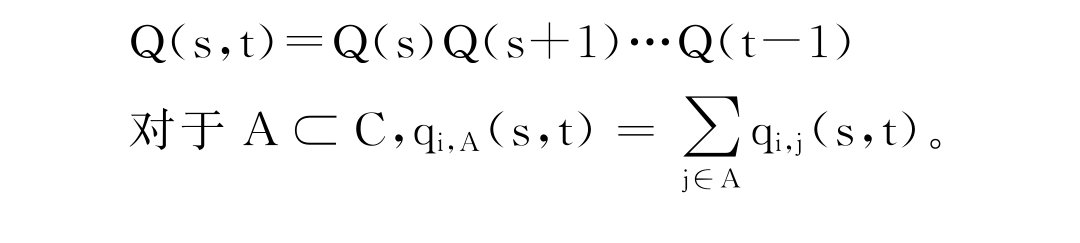
(一)有违约风险债券的价格

在风险中性概率测度下有违约风险债券的价格为:

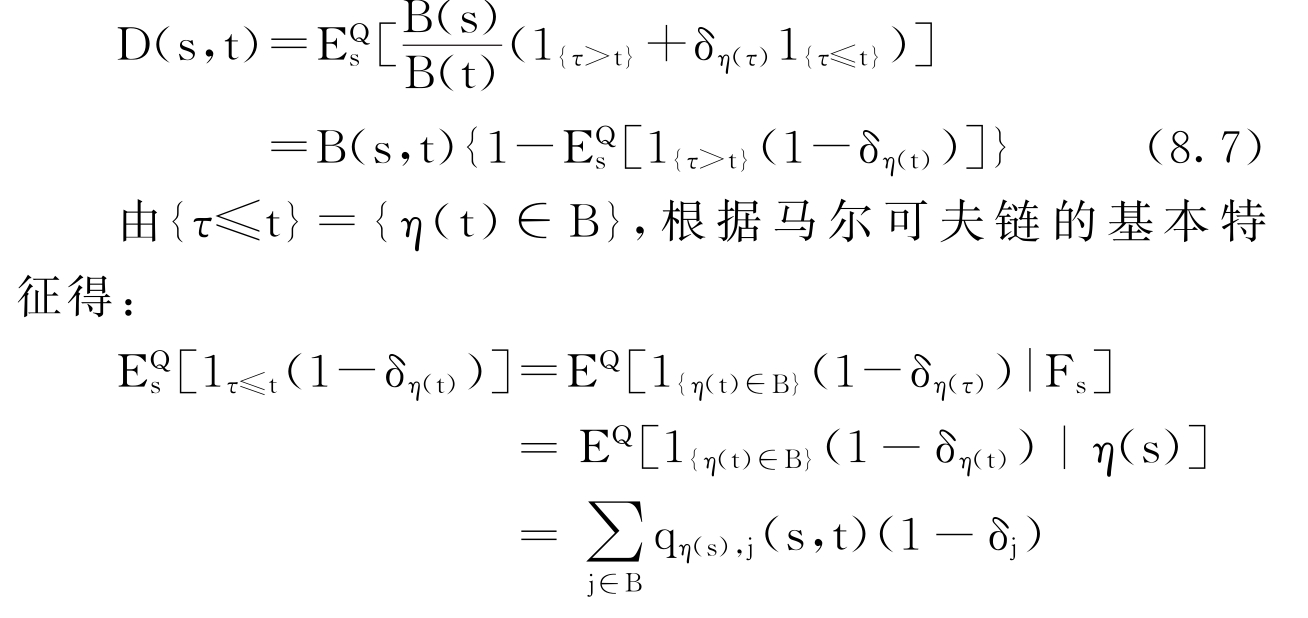
特别是,在违约状态j∈B有D_j(s,t)=δ_jB(s,t),如果q_i,B(s,t)>0,(8.9)式可写为:

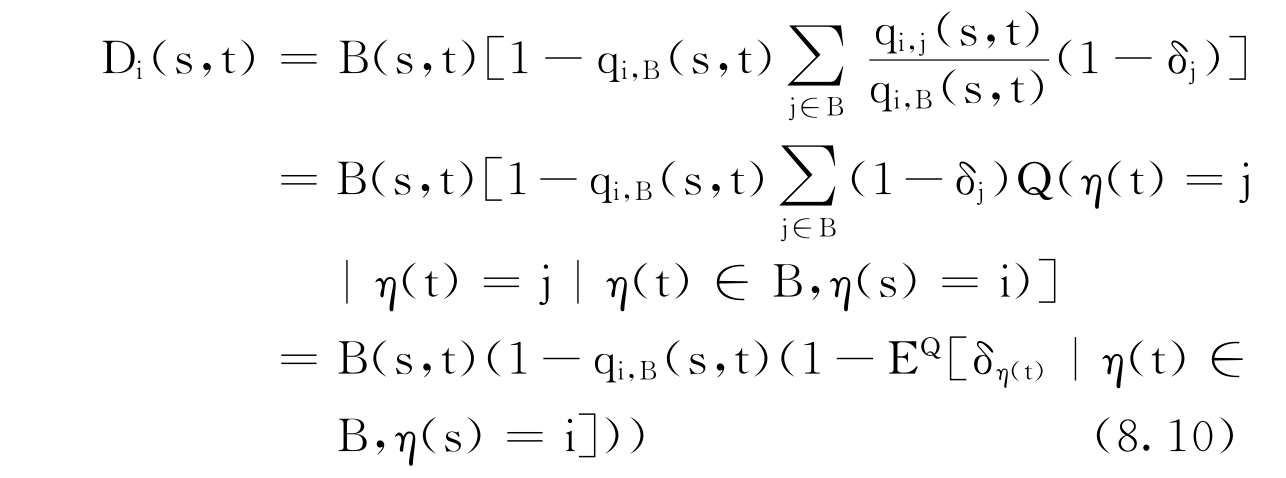
因此,有违约风险债券的价格等于无风险零息债券价值减去违约损失的现值。

(二)信用差价计算

信用等级为i∈C的贴现债券s时计算的t时(0≤s≤t≤T-1)远期利率为:

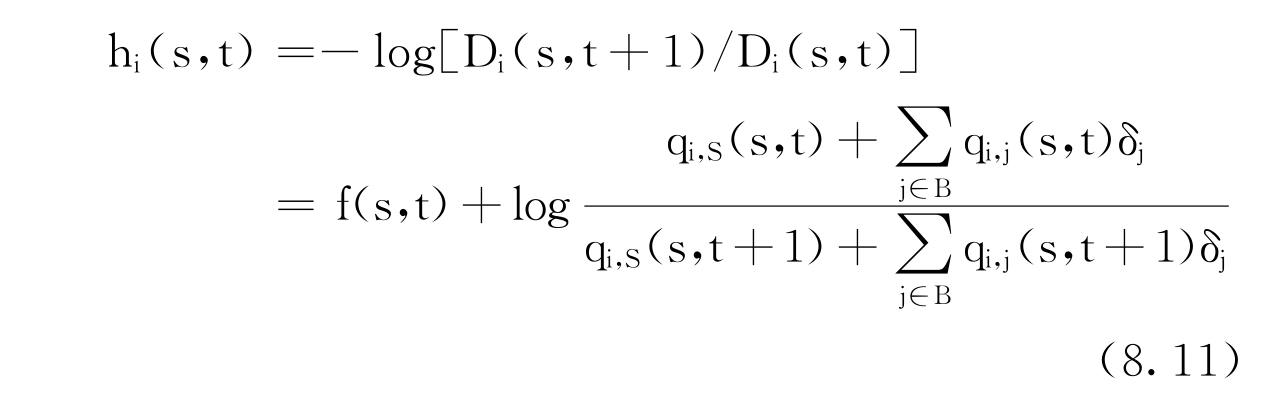
取s=t,信用等级为i∈S的贴现债券的远期利率为:

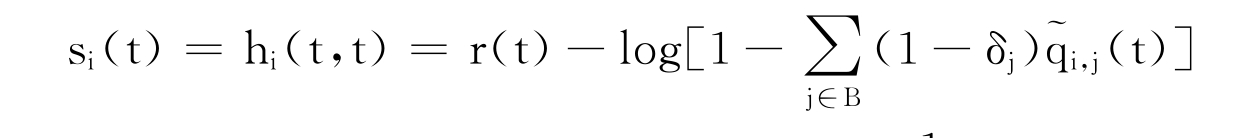
根据无风险债券到期收益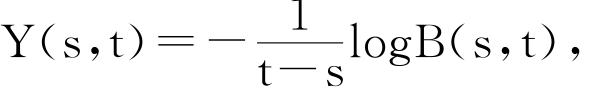0≤s≤t≤T,信用等级为i∈C的贴现债券的到期收益为:

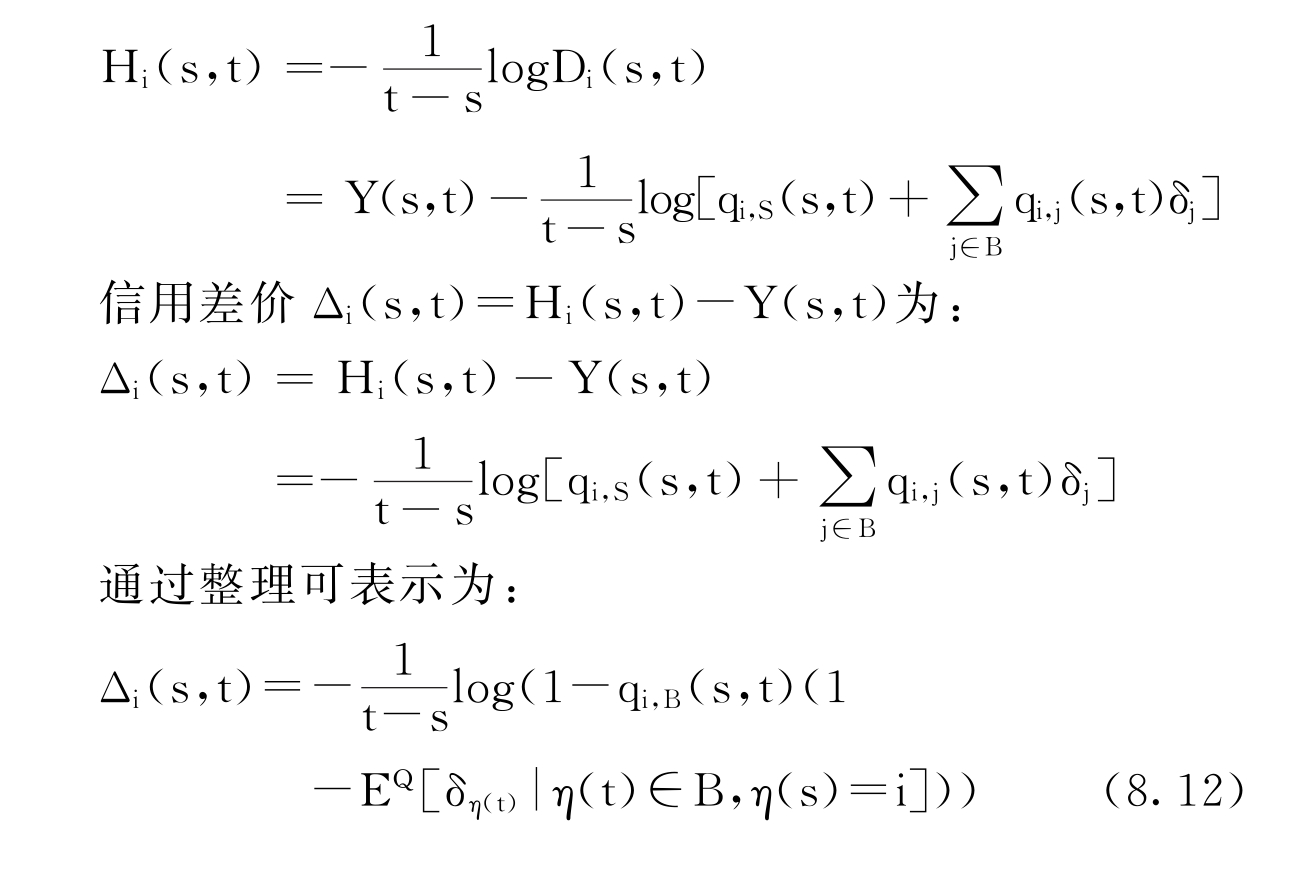
(三)风险中性转移概率的计算

为了进一步扩展Jarrow,Lando and Turnbul(1997)(JLT)模型和Kijima和Komoribayashi(1998)(KK)模型,进一步假设如下:

(1)观察到初始时刻无风险零息债券的期限结构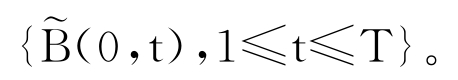

(2)观察到初始时刻任何信用等级i∈B有违约风险零息债券的期限结构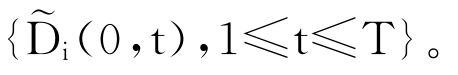

(3)不同信用等级的违约挽回率δ_i,i∈B。

(4)单期历史信用转移矩阵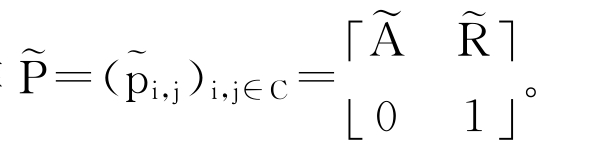

因此,对于i∈S,j∈B,通过下式计算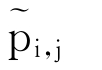

为了得到风险中性转移概率矩阵Q(t)(0≤t≤T),通过观察到的市场价格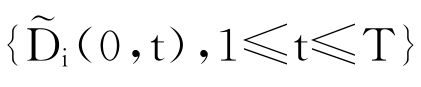倒算,有下列的关系式:

由于测度P和测度Q的等价性,下式总是成立:

q_i,j(t)=π_i,j(t)p_i,j,对于所有i,j∈C和0≤t≤T-1

π_i,j(t)为风险贴水调整,可表示为:

π_i,j(t)=π_i(t),对于所有i∈S,j∉k(i)和0≤t≤T-1(8.14)

在风险中性概率测度Q下,从0时到t+1时的转移矩阵为:

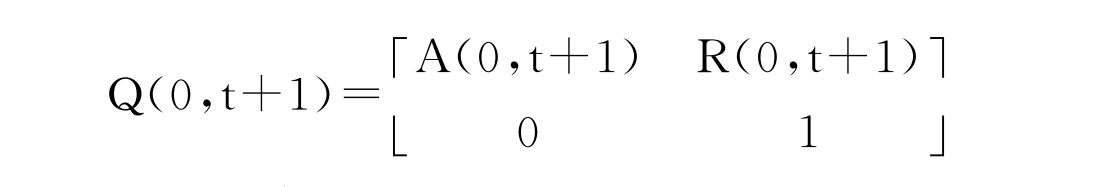
这里矩阵A(0,t+1)和R(0,t+1)可由A(s)和R(s)(0≤s≤t)来表示,由Q(0,t+1)=Q(0,t)Q(t)有A(0,t+1)=A(0,t)A(t)和R(0,t+1)=A(0,t)R(t)+R(0,t),而且,对于i∈S,(8.12)式可表示为:

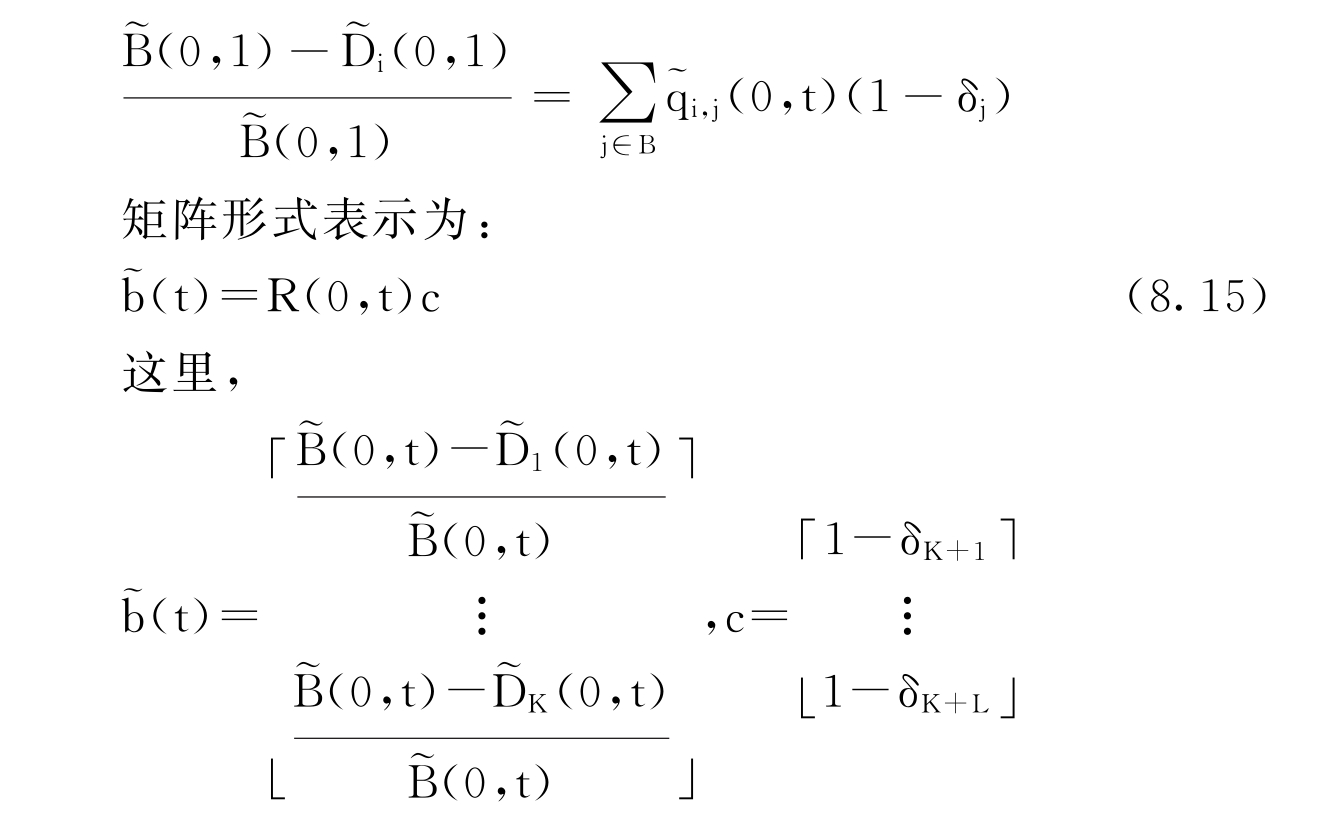
矩阵形式为:

R(0,t+1)=A(0,t)R(t)+R(0,t)

两边乘以c并根据(8.15)式,有:

以下扩展KK模型的风险中性转移概率,假设任意i∈S,i,j∈C和0≤t≤T-1,不同测度下注意概率的关系

将(8.17)式写成矩阵的形式为:

这里∏(t)=diag(π₁(t),…,π_K(t)),Γ(t)= diag(γ₁(t),…,γ_K(t)),由于Q(t)为随机矩阵,且满足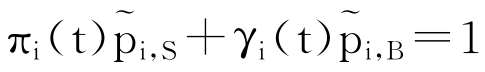,因此,有下列关系式:

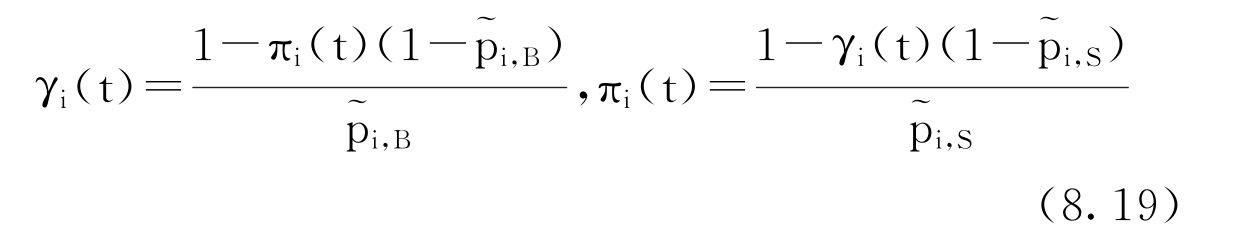
由于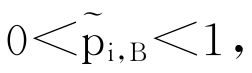上式矩阵形式为:

这里e_K、e_L分别为K、L维单位向量,由于测度P和Q等价性定义,下式必须满足:

即对于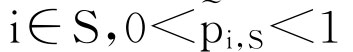必须满足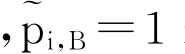表示对所有信用等级债券,下一时期违约均会发生。因此,在估计风险贴水调整时,必须检查(8.21)式是否满足。

由(8.13)式和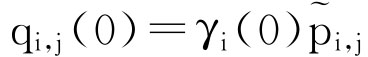,有:

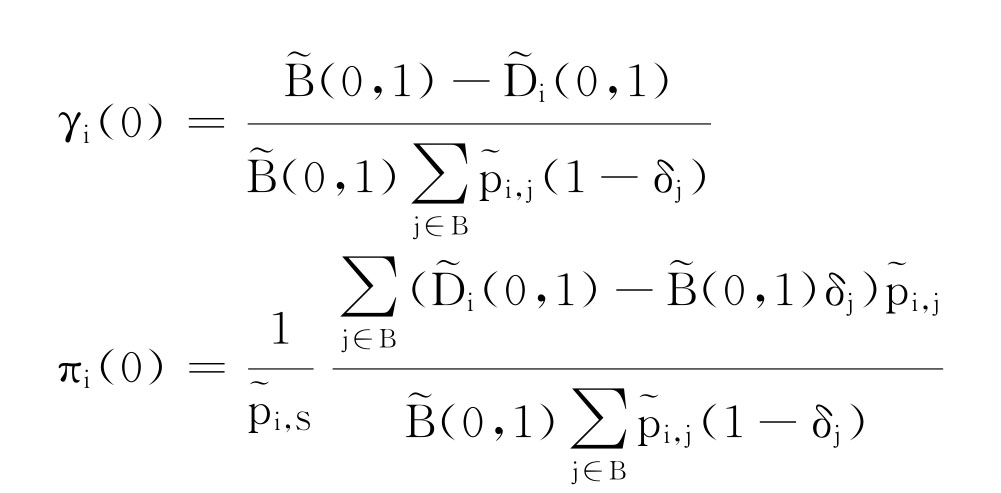
根据(8.17)式,可以得到Q(0)。假设已知Q(0),…, Q(u-1),可以计算Q(u)。由(8.16)式和(8.18)式,得下式:

因此,如果矩阵A(0,u)是可逆的,有:

w_i,j(0,u)为A-1(0,u)的每一项,上式可表示为: