随机波动率模型

三、随机波动率模型

(一)平方根均值回复模型

这里考虑平方根波动率V_t和均值回复的基础资产动态过程,在风险中性概率Q下,均值回复基础资产动态过程如下:

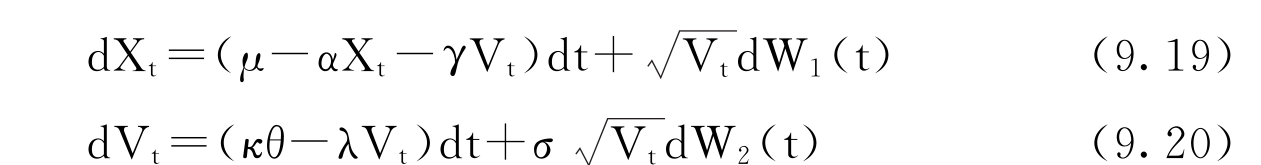
这里,d<W₁,W₂>t=ρdt,假设不变的无风险利率为r,特征函数可表示为:

当α=0时,即上式变为Zhu(2000)的方程。根据Feynman-Kac定理计算(9.20)式的期望值部分,定义函数F(t,V)为

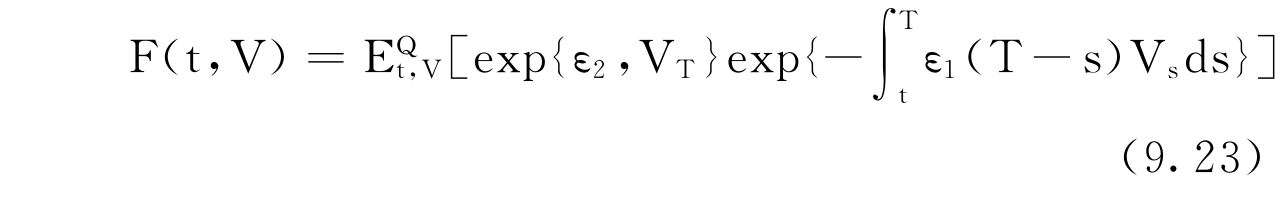
F(t,V)满足以下偏微分方程:

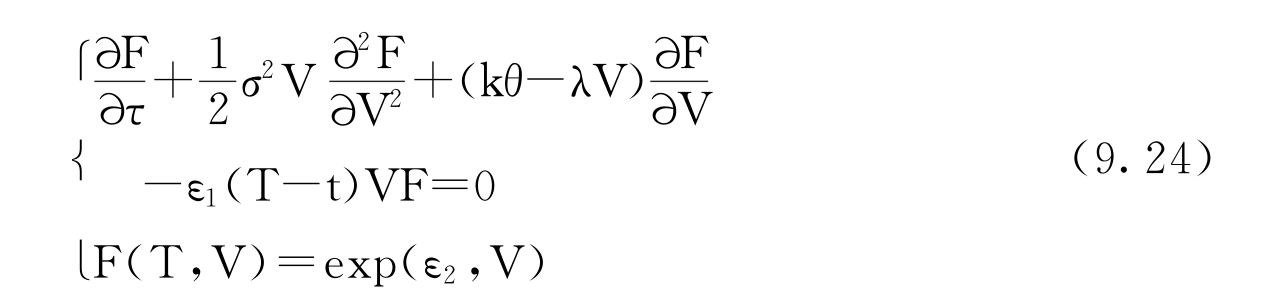
假设F(t,V)关于(τ,V)对数线性,而且可表示为

F(t,V)=exp[D(τ)V+C(τ)],τ=T-t(9.25)那么,D(τ)和C(τ)满足以下常微分方程

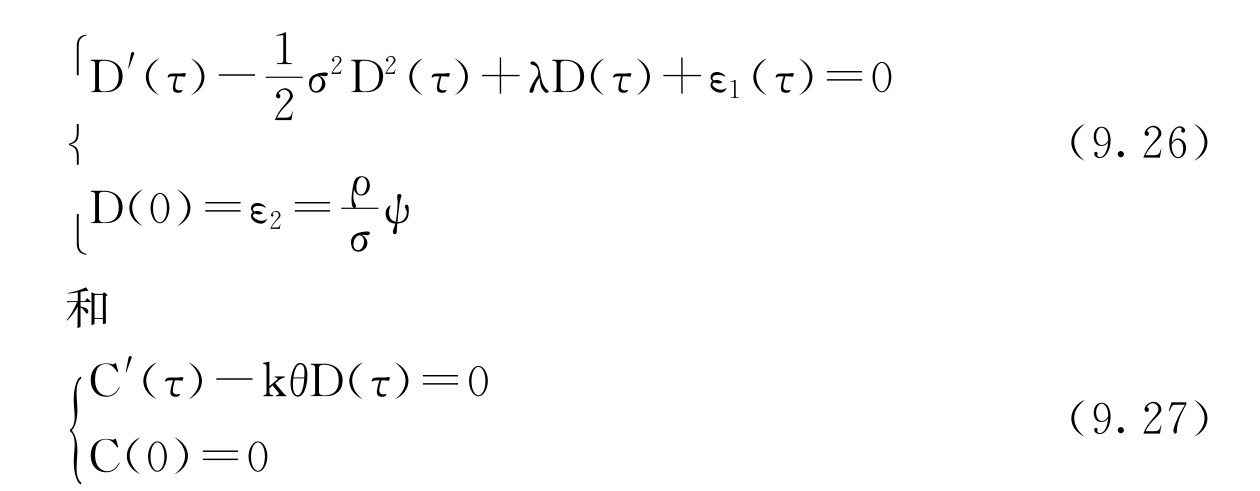
平方根均值回复模型的实际特征函数f(ψ)为:

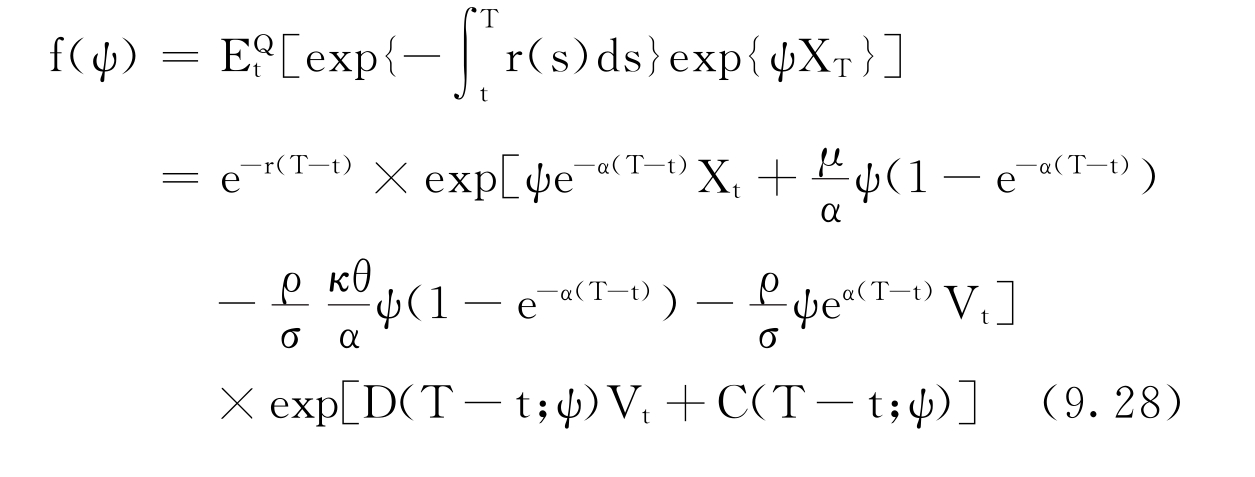
(二)Ornstein-Uhlenbeck均值回复模型

1.基础资产的风险贴水与波动率的平方σ²_t成比率

考虑在风险中性概率Q下,假设风险贴水与波动率平方σ²_t成正比,Ornstein-Uhlenbeck波动率过程和均值回复基础资产过程如下:

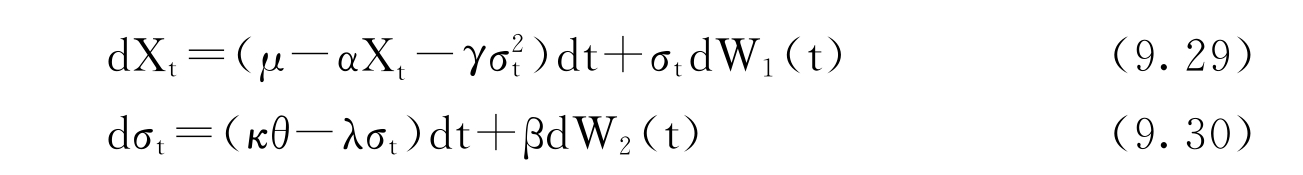
这里d<W1,W2>t=ρdt,特征函数可表示如下:

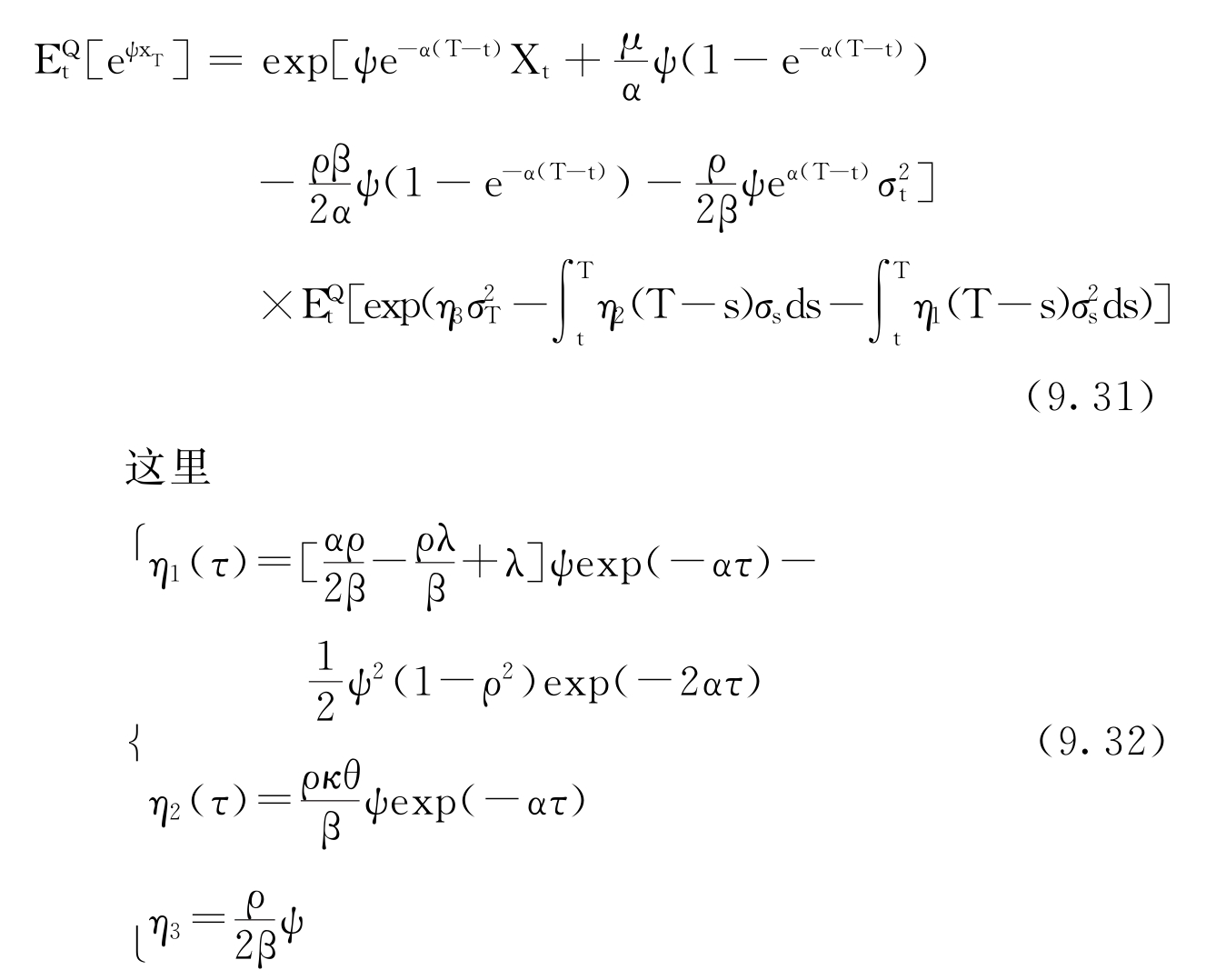
当α=0时,即上式变为前面所提Zhu(2000)的方程。定义函数G(t,σ)为

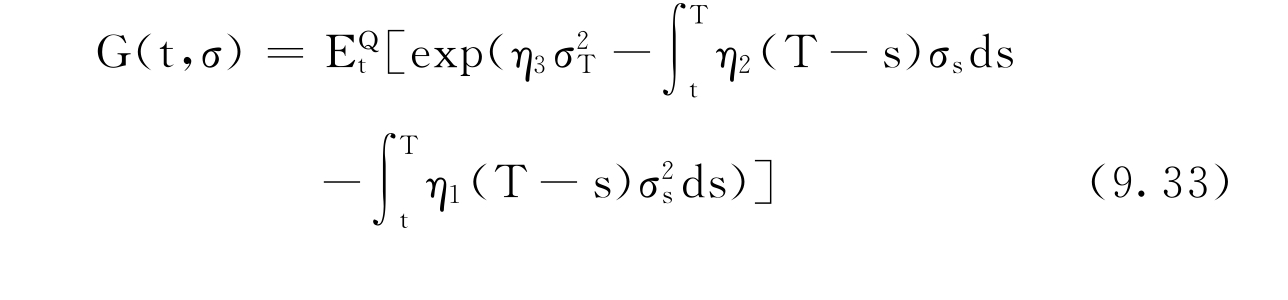
应用Feynman-Kac定理,G(t,σ)满足以下偏微分方程

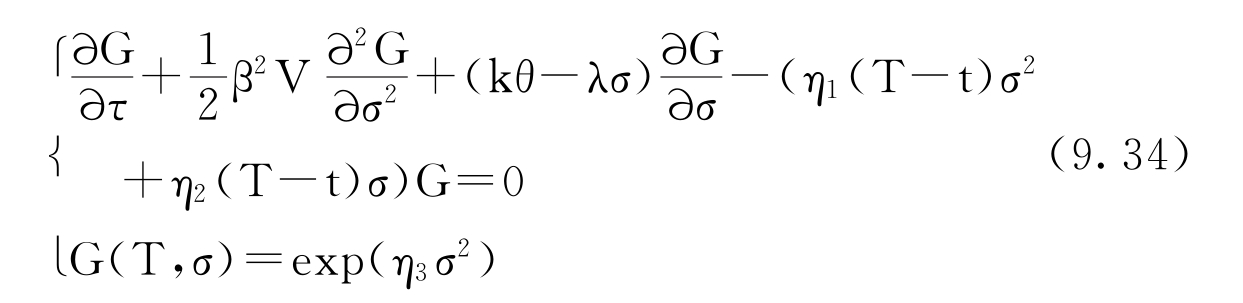
假设G(t,σ)关于(t,σ)对数线性,而且可以表示为

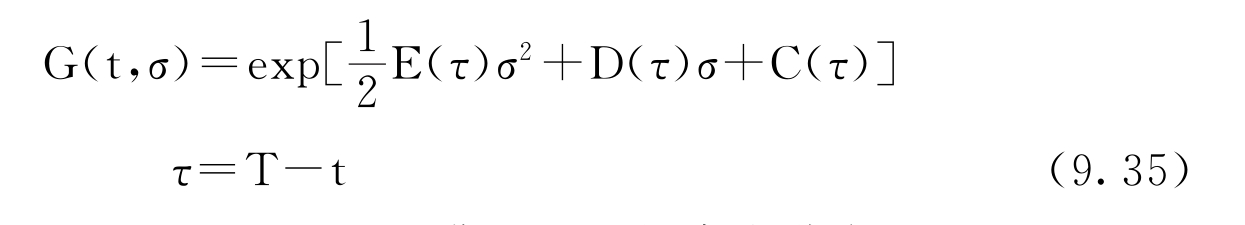
那么D(τ)和C(τ)满足以下的常微分方程

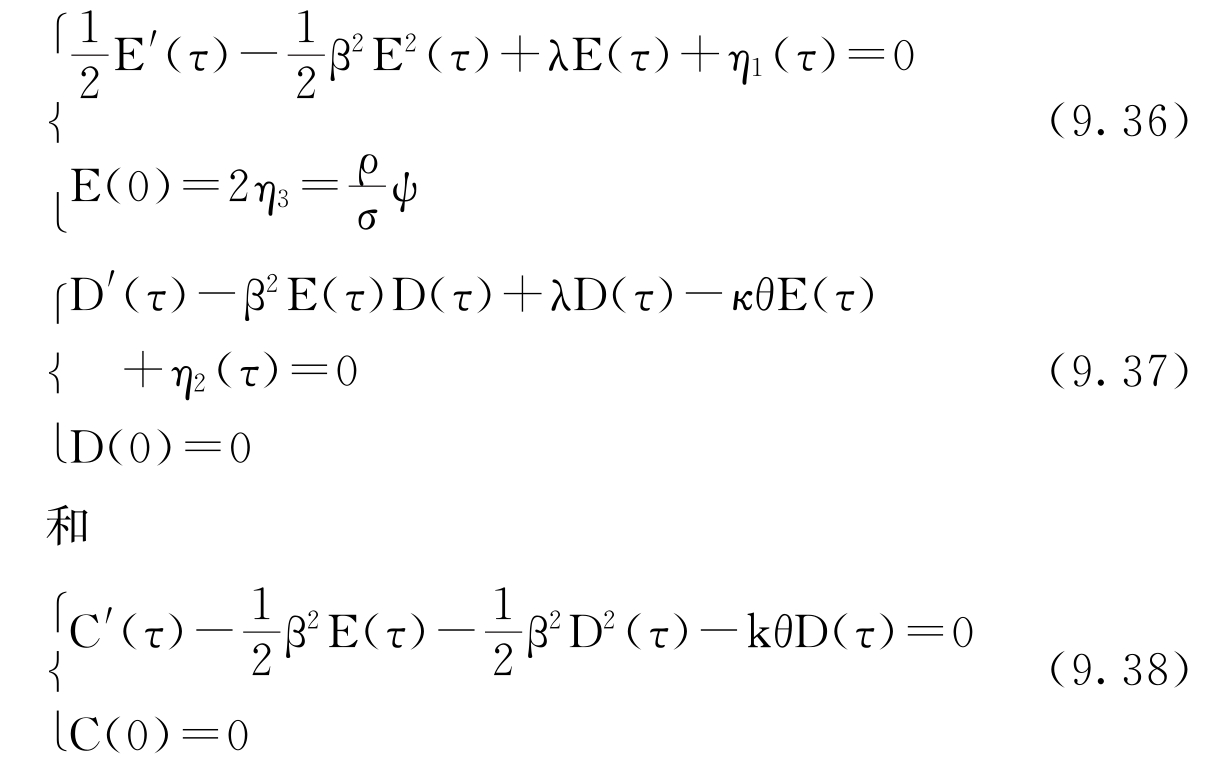
虽然李嘉图形式的方程(9.36)有解析解,但是方程(9.37)和(9.38)没有解析解,必须通过数值方法求解,实际特征函数f(ψ)为

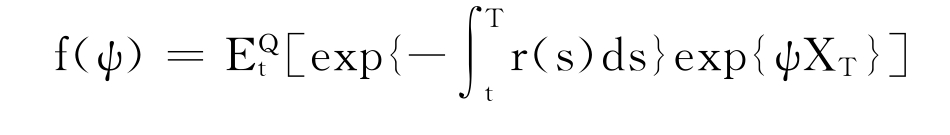
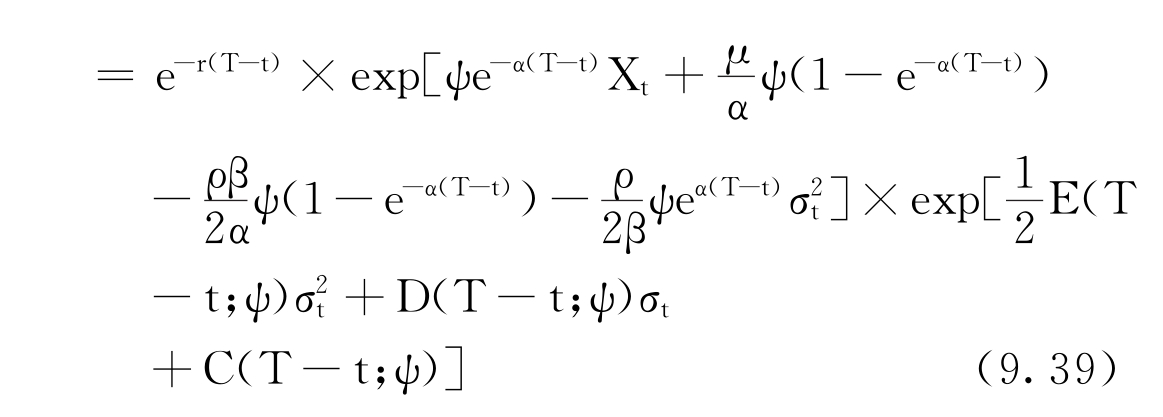
2.基础资产的风险贴水与波动率σ_t成比率

如果基础资产X_t的风险贴水与波动率σ_t成比率,上述模型的方程变为:

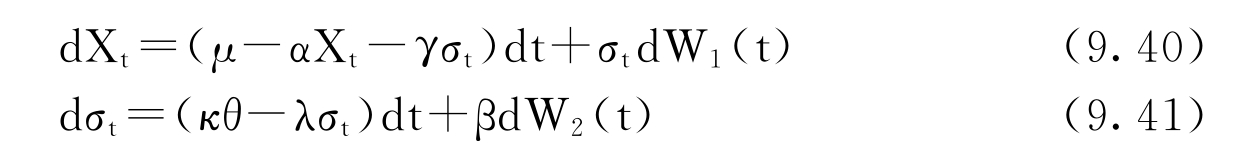
特征函数可表示如下:

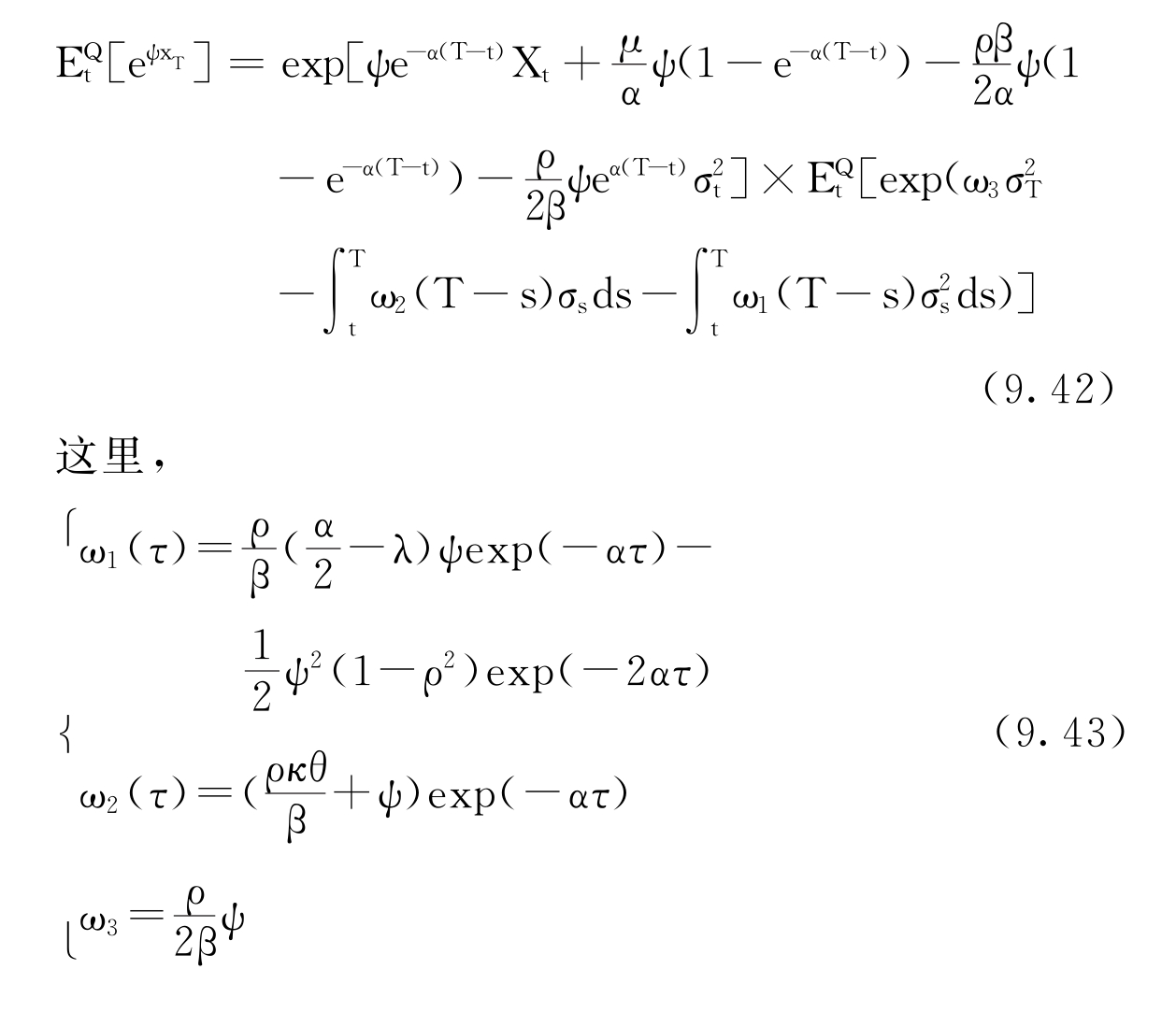
应用Feynman-Kac定理,实际特征函数f(ψ)为:

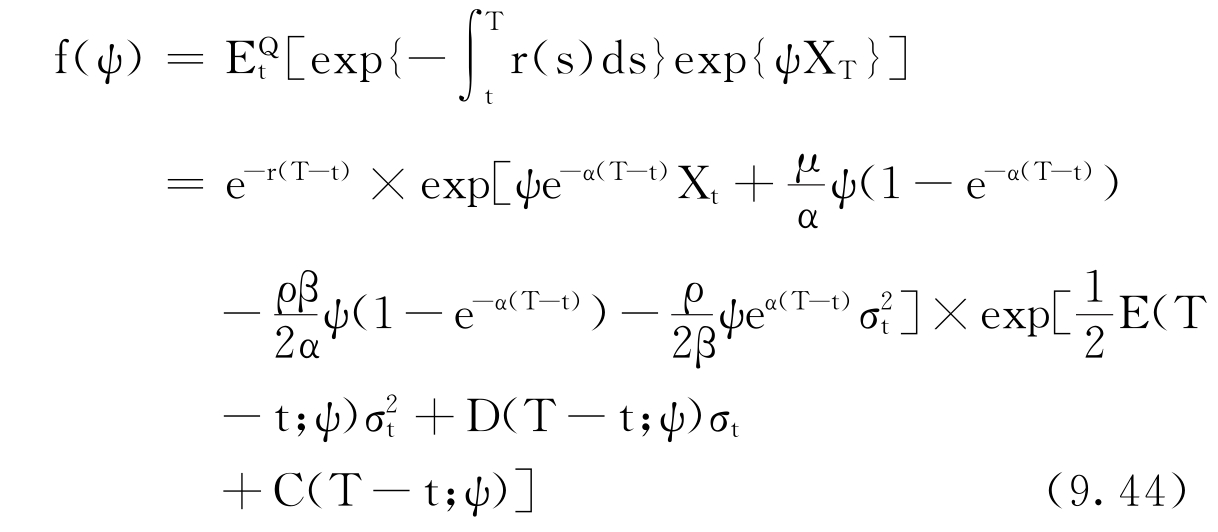
这里的E(τ)、D(τ)、C(τ)与式(9.36～9.38)相同,只是η1、η2、η3分别由ω₁、ω₂、ω₃代替。