1.二层圆均匀光波导的一般概念
二层圆均匀光波导只有芯层和包层,是一种阶跃光波导,如图4.4.1所示,其折射率分布为

其中,a为芯层半径,n1>n2。这虽然是一种最简单的光波导,但却是最重要、最有实际意义的光波导。在工程技术中广泛使用的单模光纤通常都是这种阶跃光波导,通常,其芯层直径2a为4~10μm,包层直径为125μm。虽然包层直径实际上总是有限大的,但由于介质分界面外(即包层内)的光场已迅速衰减,理论上可将包层直径看成无限大。因此,单模光纤理论上属于二层圆均匀光波导。
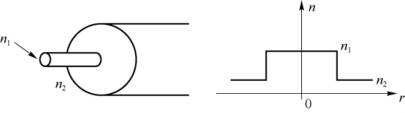
图4.4.1 折射率为阶跃型分布的二层圆均匀光波导
作为一种简单的圆均匀光波导,二层圆均匀光波导的模式场具有圆对称性。用不同的坐标分解法分解,可以得到不同的矢量模和线偏振模,其中,矢量模的求解归结为求解方程组(4.3.5)中前两个关于纵向分量的方程:
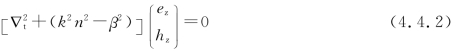
求出纵向分量ez,hz后,利用横向分量和纵向分量的关系式(4.3.9)求出横向分量。标量模的求解归结为求解方程式(4.3.19)
![]()
或
![]()
求出横向分量ey(或ex)后,利用方程组(4.3.20)求出其他分量。
在极坐标系中
![]()
于是,可将式(4.4.2)~式(4.4.4)一并写为
![]()
下面来讨论二层圆均匀光波导的矢量模解,主要讨论电磁波解(场分布)、特征方程、截止条件和色散曲线。
2.矢量模的电磁波解
式(4.4.5)可以用分离变量法求解。设上式的解可写为
![]()
其中,R(r)是波导半径r的函数,Φ(φ)是截面圆心角的函数,指数e-iβz表示这个解是沿z轴的行波。将上式代入方程(4.4.5),两边同乘以r2/(RΦ),得
![]()
其中,左边只是r的函数,右边只是φ的函数,r与φ是相互独立的变量,因此,上式成立的条件是两边同等于一个常数,设此常数为m2。于是,由上式右边得
![]()
上式的解是
![]()
为保证Φ(φ)是周期为2π的单值解,m应为正整数m=0,1,2,…由方程(4.4.7)左边得
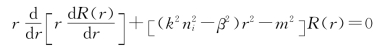
做变换x=![]() 上式变为
上式变为
![]()
当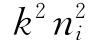 -β2>0时,上式是标准的m阶贝塞尔方程;当
-β2>0时,上式是标准的m阶贝塞尔方程;当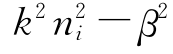 <0时,上式是变型(虚宗量)m阶贝塞尔方程。
<0时,上式是变型(虚宗量)m阶贝塞尔方程。
在芯层中,折射率较n1大,设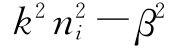 >0,方程(4.4.10)的解是
>0,方程(4.4.10)的解是
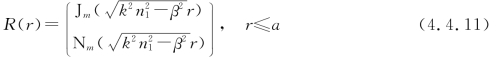
其中,Jm,Nm分别是第一、第二类(Neumann)贝塞尔函数。当x足够大时,其大宗量渐进式为
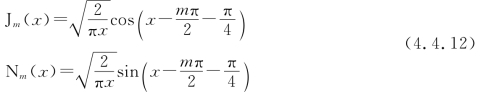
当x足够小时,其小宗量渐进式为
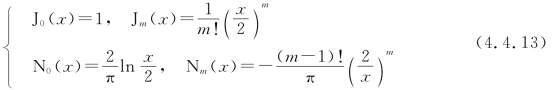
函数曲线如图4.3.3(a)和(b)所示。由图可见![]() 在芯层中(0≤r≤a)总是有限值,而
在芯层中(0≤r≤a)总是有限值,而![]() 当r→0是发散的。因此,应取
当r→0是发散的。因此,应取
![]()
将上式和式(4.4.9)代入式(4.4.6),得芯层中的纵向分量
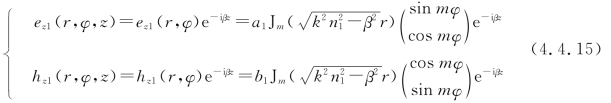
其中,ez取因子sin mφ时,hz取因子cos mφ;ez取因子cos mφ时,hz取因子sin mφ,以保证在芯层和包层的分界面上ez和hz满足介质边界条件(具体讨论见后)。
在包层中,折射率n2较小,设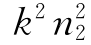 -β2<0,方程(4.4.10)的解是
-β2<0,方程(4.4.10)的解是
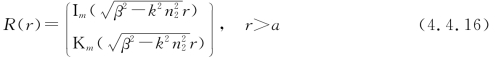
其中,Im,Km分别是第一、第二类(Neumann)变型贝塞尔函数。当x足够大时,其大宗量渐进式为
![]()
当x足够小时,其小宗量渐进式为
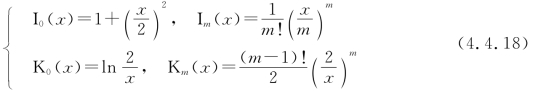
函数曲线如图4.3.3(c)和(d)所示。由图可见,当r→∞时,Im![]() 在包层中发散,而Km
在包层中发散,而Km![]() 按指数趋于零,因此,应取
按指数趋于零,因此,应取
![]()
将式(4.4.19)和式(4.4.9)代入式(4.4.6),得包层中的纵向分量
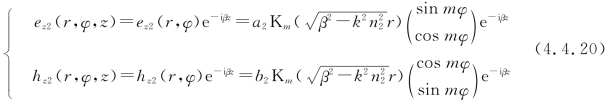
因子sin mφ和cos mφ的选取规则与式(4.4.15)相同。为明确起见,在式(4.4.15)和式(4.4.20)中选取因子sin mφ和cos mφ分别作为ez和hz的因子,并利用横向参数的定义式(4.2.14),将芯层和包层中的纵向分量写成
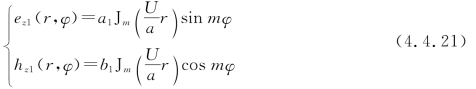
和
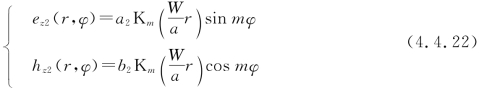
芯层和包层中的电磁波解必须满足介质边值条件,即电场和磁场的切线分量在界面上连续。因此,r=a时,应有ez1=ez2,hz1=hz2,也就是
![]()
为便于运算,令
![]()
于是有
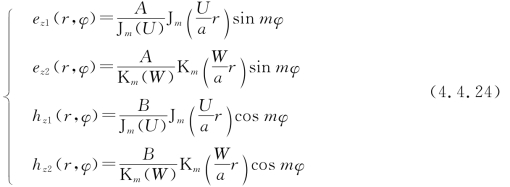
将这四个式子代入式(4.3.9),得芯层中模式场的其余分量
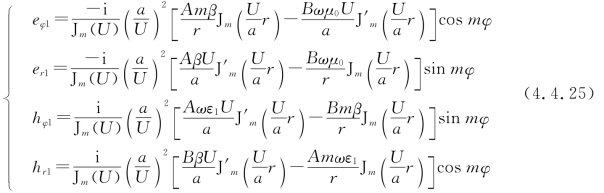
和包层中模式场的其余分量
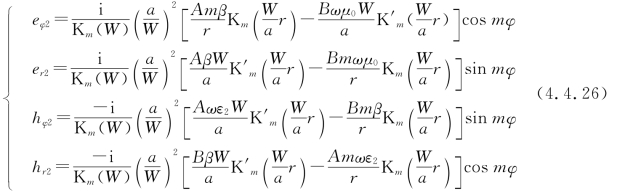
因为电场和磁场的切线分量在界面上连续,即当r=a时,
![]()
有
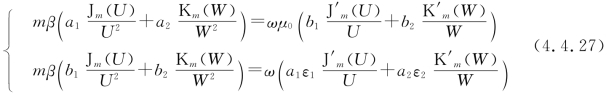
显而易见,在波导结构常数a,ε1,ε2,μ0和激励条件ω,β给定时,即当特征参数U,W给定时,第m个模式的4个待定常数a1,a2,b1,b2由式(4.4.23)和式(4.4.27)的4个方程确定。
3.特征方程
为得到矢量模特征方程,我们把r=a时的边值关系eφ1=eφ2,hφ1=hφ2写成
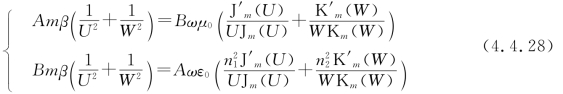
其中,用到了关系式ε=n2ε0。将这两式相乘,消去常数A,B,得
![]()
利用特征参数的定义式(4.2.14)可以消去上式中的传输常数β,得
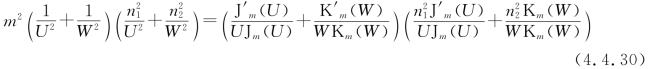
以上两式确定特征参数U,W,称为矢量模的特征方程。注意到式(4.2.15)
![]()
在已知波导结构常数和波长时,可由式(4.4.30)解出特征参数U,W。
以上是未做任何近似的精确结论。若包层折射率n2只是略小于芯层折射率n1,这种光纤称为弱导光纤,实际通讯中使用的光纤都是弱导光纤。弱导条件可写成n1/n2≈1,于是,式(4.4.30)化为
![]()
其中,m=0,1,2,…这就是弱导条件下的特征方程,是分析弱导光纤传输特性的基础。
对于TE模,ez=0,即式(4.4.24)中的常数A=0。因此,由边值关系(4.4.28)第二式
得
![]()
显然,β≠0![]() ≠0,而B也不能等于零,因为B若再等于零,就没有电磁场了。故只能是m=0。这与4.3节的结论一致。令m=0,由式(4.4.28)第一式或式(4.4.31)得
≠0,而B也不能等于零,因为B若再等于零,就没有电磁场了。故只能是m=0。这与4.3节的结论一致。令m=0,由式(4.4.28)第一式或式(4.4.31)得
![]()
这就是TE模的特征方程。利用贝塞尔函数的递推公式
![]()
可将TE模的特征方程写成下面常见的形式:
![]()
对于TM模,hz=0,即式(4.4.24)中的常数B=0,由边值关系式(4.4.28)第一式得m=0。令m=0,由(4.4.28)第二式得
![]()
这就是TM模的特征方程。在弱导条件下n1/n2≈1,式(4.4.34)与式(4.4.33)一致,或者说,式(4.4.33)是弱导条件下TE模和TM模共同的特征方程。m=0意味着电磁波的场量与角度φ无关,即场量在波导横截面内是轴对称分布。
若m≠0,则由边值关系式(4.4.28)可知A≠0,B≠0,即ez≠0,hz≠0。与式(4.4.31)中的“+”号对应着的一组解称为EH模,与“-”号对应着的一组解称为HE模,它们的特征方程是
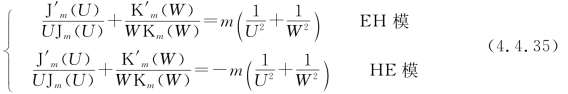
利用贝塞尔函数递推公式
![]()
![]()
可将式(4.4.35)化为

在式(4.4.36)中,若令m=0,利用递推公式
![]()
可将式(4.4.36)的两个式子都写成
![]()
这就是弱导条件下TE模和TM模共同的特征方程(4.4.33)。所以,TE模和TM模是EH模和HE在弱导条件下的特例。如前所说,TE模和TM模都是偏振方向相互垂直的线偏振波,而EH模和HE模是偏振方向不相互垂直[见式(4.2.3)]的椭圆偏振波。可以证明,HE模偏振旋转方向与波行进方向一致,符合右手法则;EH模偏振旋转方向与波行进方向相反。从场强关系看,EH模中电场较磁场强,HE模中磁场较电场强。从相位关系看,EH模中hz分量超前于ez分量90°,HE模中hz分量落后于ez分量90°。从光线理论的意义上说,电场垂直于子午面的子午光线对应于TE模,如图4.4.2(a)所示;磁场垂直于子午面的子午光线对应于TM模,如图4.4.2(b)所示;偏斜光线只能对应于混合模。
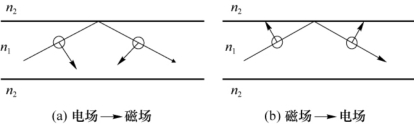
图4.4.2 电场(或磁场)垂直于子午面的子午光线对应于TE模(或TM模)的示意图
4.截止条件
如前所说,一个模式的纵向传播特性由纵向传播常数β描述,横向传播特性由参数m,U,W描述,其中m描述场量沿角度φ的分布,U描述芯层内场量沿半径方向的分布,而W描述包层内场量沿半径方向的分布。β,U,W之间的关系由定义式(4.2.14)给出。只要由特征方程求出这三个参数中的一个,其他两个就可由式(4.2.14)得到。
如果忽略波导中材料的吸收损耗,模式沿纵向传播无衰减,则U和W都应是正实数。W是正实数时,如前所说,包层内场量沿半径方向按指数快速衰减,W越大,衰减越快,电磁场能量就越集中在芯层内。反之,W越小,就有越多的电磁场能量传播到包层内。如果W是虚数(W2<0),包层内的场量用汉克尔函数Im描述,模式成为沿径向辐射的辐射模。所以,W=0是一个模式是导波模还是辐射模的临界点。将W=0时的径向相位常数U记作Uc,归一化频率V记作Vc,Uc和Vc就是导波的截止参数。于是,W=0时有Uc=Vc。
(1)TE模和TM模
如前所说,弱导条件下TE模和TM模共同的特征方程是式(4.4.33):
![]()
由式(4.4.18)有
![]()
于是得
![]()
注意到J1(U)总为有限值,则TE模和TM模在截止状态的特征方程是
![]()
由式(4.4.13)可知,J0(U)=1,J1=![]() ,因此,若U=0,则c
,因此,若U=0,则c
![]()
这与式(4.4.37)矛盾,所以,只能是
![]()
这说明截止状态时的归一化频率Vc和径向传播常数Uc是零阶贝塞尔函数的零点(或根)μ0n,即
![]()
前几个零点值是μ0n=2.405,5.520,8.654,…每一个零点值对应着一个TE模和TM模,记作TE0n模和TM0n模,其归一化截止频率Vc=μ0n。
电磁波在结构参数a,n1,n2给定的波导中传播时,若波长λ给定,则其截止归一化频率![]() 也是确定的。若对某个模式,V>Vc,必有W2>0,该模式是导波模。反之,若V<Vc,必有W2<0,该模式是辐射模。也就是说,模式在波导中传播的条件是
也是确定的。若对某个模式,V>Vc,必有W2>0,该模式是导波模。反之,若V<Vc,必有W2<0,该模式是辐射模。也就是说,模式在波导中传播的条件是
![]()
其中,λc称为该模式的截止波长。
序号n相同的TE0n模和TM0n模有相同的截止参数,称为一对简并模。在所有的TE0n模和TM0n模中,TE01模和TM01模的截止归一化频率最小,等于2.405,对应截止波长λc最大,其值是
![]()
例如,某光纤的半径a=4.0μm,Δ≈0.003,纤芯折射率n1=1.48,则截止波长λc≈1.20μm。所以,若光纤中传播的光的波长λ=1.31μm,则其模式必不是TE01模和TM01模。
(2)EH模
弱导条件下EH模的特征方程是式(4.4.36)中的第一式:
![]()
利用式(4.4.18)的最后一个式子,得
![]()
于是,EH模在截止状态的特征方程是
![]()
由式(4.4.13)可知![]() 若U→0,则有c
若U→0,则有c
![]()
这与式(4.4.42)矛盾,所以,只能是
![]()
这说明截止状态时的归一化频率Vc和径向传播常数Uc是m阶贝塞尔函数的零点μmn,即
![]()
m阶贝塞尔函数第n个零点对应的EH模记作EHmn模。
表4.4.1中列出了贝塞尔函数的前几个零点。从表中可以看出,n≠0时,最小的零点值是μ11=3.832,也就是说,在EHmn模序列中,EH11模的归一化截止频率最小:Vc=Uc=3.832,而其截止波长最长:
![]()
对于前面所说的例子,a=4.0μm,Δ≈0.003,n1=1.48,则截止波长λc=0.75μm。所以,波长为1.31μm和0.85μm的光都不能以EH11模在光纤中传播。
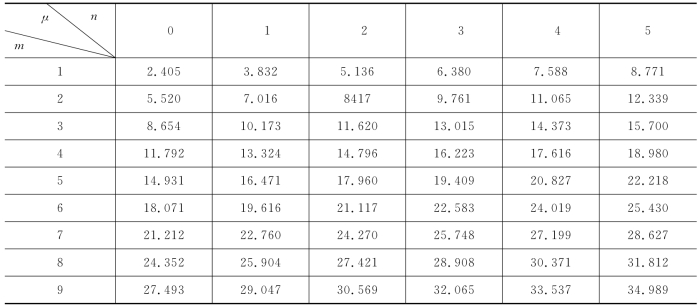
表4.4.1 Jn(x)(n=0,1,2,3,4,5)的前9个正零点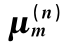 的近似值
的近似值
(3)HE模
弱导条件下HE模的特征方程是(4.4.36)中的第二式:
![]()
当m=1时,利用式(4.4.18)的后两式得
![]()
于是,m=1时HE模在截止状态的特征方程是
![]()
由式(4.4.13)可知:
![]()
所以,Uc=0和Uc=μ1n都是方程(4.4.46)的解。以Vc=0和Vc=μ1n为归一化截止频率的HE模记作HE1n。为了将Vc=0的模作为HE1n序列模的第一模,而将其归一化截止频率记作
![]()
比较式(4.4.47)和式(4.4.44),可知HE1,n+1模和EH1n模的归一化截止频率相同,即HE1,n+1模和EH1n模是简并模。
注意HE11模的归一化截止频率Vc=0,截止波长λc=∞。这表明HE11模不会截止,可以任意低的频率在光纤中传播,称为光纤中的主模(或基模)。不过,如果频率过低(即波长过长),HE11模的能量将大量传向包层中,损耗加大,实际上是难以有效传输的。
当m≥2时,利用式(4.4.18)的最后一式,由式(4.4.45)得
![]()
即
![]()
由贝塞尔函数的递推公式2mJm(U)=UJm-1(U)+UJm+1(U)得
![]()
即
![]()
由上式和式(4.4.48)得
![]()
由于Jm-2(Uc)与Jm(Uc)线性无关,上式只有在Jm-2(Uc)与Jm(Uc)都等于零时才成立,故得
![]()
这表明,对于m≥2的HE模,归一化截止频率是
![]()
其中,m=2,3,…,n=1,2,…
以上两式还表明,m=2时,HE2n模与TE0n模、TM0n模有相同的归一化截止频率,它们是简并模。m=3时,HE3n模与EH1n模、HE1,n+1模有相同的归一化截止频率,它们是简并模。m≥4时,HEmn模与EHm-2,n模的归一化截止频率相同,它们也是简并模。总之,若将所有截止频率相同的模式归为一组,按照截止频率从低到高排列,前34个模式如表4.4.2所示。每组中的模式数的计算方法是,TE0n模和TM0n模是轴对称模式,每个TE0n模和TM0n模只是一个模式;所有的混合模EHmn模和HEmn模在横截面上可以取因子cos mφ和sin mφ,故每个混合模是二重简并的。
(4)单模条件
如前所说,HE11模的归一化截止频率Vc=0,截止波长λc=∞,它是光纤中的主模。
表4.4.2 模式组及其归一化截止频率
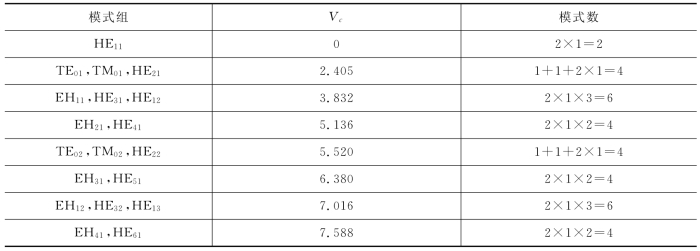
从表4.4.2可以看出,次最低阶模是TE01模、TM01模和HE21模,它们的归一化截止频率为2.405。如果适当设计光纤并选择工作波长λ,使归一化工作频率满足条件
![]()
或
![]()
则TE01模、TM01模和HE21模及所有的高阶模都截止,只有HE11模可以传输。式(4.4.53)称为光纤单模条件。
光纤通信的工作波长总是选1.31μm和1.55μm这两个低损耗波长。若以1.31μm为工作波长,并取Δ≈0.003,n1=1.46,则光纤的纤芯半径应满足条件
![]()
因此,光纤的纤芯直径通常在8~9μm。
5.远离截止状态时导模的性质
如果归一化频率V远大于截止频率Vc,则导波模的能量几乎全部集中在芯层中,这种状态称为远离截止状态。多模光纤的归一化频率V很大,其中的低阶模可看作处于远离截止状态,并表示为V→∞。由于V=![]() ,V→∞相当于
,V→∞相当于![]() →∞,这时,电磁波近似于在无界介质中传播的平面波,其横向传播常数γ很小,纵向传播常数β趋于kn1。因此,W2=a2(β2-k2n22)→k2a2(n21-n22)=V2,也就是说,V→∞时W→∞,导波模的能量几乎全部集中在芯层中。W→∞时,第二类变型贝塞尔函数的渐进表示式是式(4.4.17):
→∞,这时,电磁波近似于在无界介质中传播的平面波,其横向传播常数γ很小,纵向传播常数β趋于kn1。因此,W2=a2(β2-k2n22)→k2a2(n21-n22)=V2,也就是说,V→∞时W→∞,导波模的能量几乎全部集中在芯层中。W→∞时,第二类变型贝塞尔函数的渐进表示式是式(4.4.17):
![]()
这个表示式适用于所有的m。
(1)TE0n模和TM0n模
将式(4.4.55)代入TE模和TM模的特征方程式(4.4.33),得
![]()
即
![]()
这表示远离截止状态时,TE0n模和TM0n模的径向传播常数是一阶贝塞尔函数的零点,记作:
![]()
考虑到截止状态,可知TE0n模和TM0n模径向传播常数U的取值范围是μ0n~μ1n。也就是说,接近于截止状态时,U接近于μ0n,远离截止状态时,U接近于μ1n。
(2)EHmn模
将式(4.4.55)代入EH模的特征方程(4.4.36)的第一式,得
![]()
即
![]()
这表示远离截止状态时,EHmn模的径向传播常数是m+1阶贝塞尔函数的零点,记作
![]()
考虑到截止状态,可知EHmn模的U值范围是μmn~μm+1,n。
(3)HEmn模
同理,将式(4.4.55)代入HE模的特征方程(4.4.36)中的第二式,得
![]()
这表示远离截止状态时,HEmn模的径向传播常数是m-1阶贝塞尔函数的零点,记作
![]()
考虑到截止状态,可知HE1n模的径向传播常数U的取值范围是μ1,n-1~μ0,n,也就是说,HE11模的U值范围是0~2.405,HE12模的U值范围是3.832~5.520,等等。m≥2时,HEmn模的U值范围是μm-2,n~μm-1,n。
6.色散曲线
由式(4.2.14)得
![]()
在给定归一化频率V的条件下,将式子V2=U2+W2与所考虑的模式的特征方程联立,即可解得径向传播常数U,然后由式(4.4.59)即可得到β。这样一来,就可做出一个模式的β~V函数曲线。知道了β~V函数,就可得到电磁波的相速度
![]()
和群速度
![]()
也就是得到了导波模的色散特性。故而称β~V函数曲线为波导的色散曲线。如果某模式的β~V函数曲线是直线,则表明该模式无色散,但无色散模在介质波导中是不存在的。实际的导波模,不论是TE模、TM模,还是EH模和HE模,都是有色散的,它们的纵向传播常数β都是参数V的复杂函数。
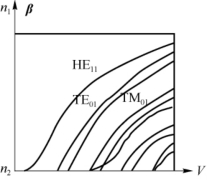
图4.4.3 几个低阶模的色散曲线图
图4.4.3是几个低阶模的色散曲线。图中以归一化频率数V为横轴,以归一化常数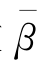 =β/k为纵轴。由图可见,所有模式的归一化常数
=β/k为纵轴。由图可见,所有模式的归一化常数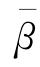 在截止时趋于包层折射率n2,远离截止时趋于芯层折射率n1,也就是说,所有模式的常数β的取值范围是
在截止时趋于包层折射率n2,远离截止时趋于芯层折射率n1,也就是说,所有模式的常数β的取值范围是
![]()
7.导波模的场型图
根据电磁场分量的表示式(4.4.24)和式(4.4.25),若得到了一个模式的参数U,W和β,除了一个待定的振幅常数外,这个模式的各个电磁场分量就确定了。据此,采用矢量合成法,可以画出由电力线和磁感线组成的模式的电磁场分布图,称为场型图。图4.4.4是TE01模和HE11模在波导横截面内的场型图。
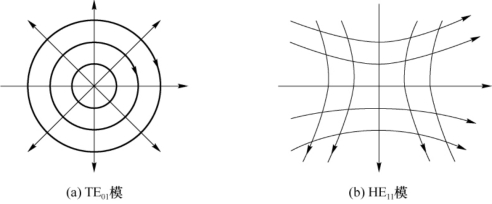
图4.4.4 TE01模和HE11模在波导横截面内的场型图
如前所说,TE01模和TM01模只有三个分量,而且是轴对称的,它们的场型图最简单。TE01模的电力线是环绕芯层中心轴的同心圆,中心处电场为零,沿着半径r向外电场增强,在某处达到极大,再逐渐减弱。减弱的快慢由参数V决定,V越大,减弱越快。将TE01模的电力线和磁感线互换,即得TM01模的场型图。TE01模和TM01模的横向场量沿着半径r有一个极大点,TE02模和TM02模有两个极大点,TE0n模和TM0n模有n个极大点。这些极大点与零点相间分布。一般地说,模序号m和n分别是极大点与零点的个数。注意,场分量沿圆周按cos mφ或sin mφ变化,合成量可能不按cos mφ或sin mφ变化,HE11就是一个例子。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















