图的定义与基本术语

7.1　图的定义与基本术语

7.1.1　图的定义

图是一种比较复杂的非线性结构。在图结构中,数据元素通常称为顶点（vertex）,每个顶点既可以有多个直接前驱结点,也可以有多个直接后继结点,顶点之间是“多对多”的关系,顶点与顶点间的关系用连接两个顶点的边表示。图是由顶点的集合和顶点之间的边的集合组成的,图的二元组表示可定义为以下形式。

G＝（V,R）

其中,V是顶点的非空有穷集合；R是边（弧）的有穷集合。从逻辑上看,图由顶点和边组成,边反映出顶点之间的联系。

若图中所有的边都用有序偶对来表示,即图中的每条边都是有方向的,此时的图称为有向图。有向图的二元组表示可定义为如下形式。

G＝（V,R）

V＝{x｜x∈elemtype}

R＝{〈x,y〉｜x∈V,y∈V}

其中,〈x,y〉表示从x到y的一条有向边,x为初始点,y为终端点。在有向图中,〈A,B〉和〈B,A〉是不一样的。图7－1所示的是一个有向图,图中边的方向是用从起始点指向终点的箭头表示的,该图的顶点集和边集分别如下。

V＝{v₁,v₂,v₃,v₄,v₅,v₆,v₇}

R＝{〈v₁,v₂〉,〈v₁,v₃〉,〈v₂,v₄〉,〈v₂,v₅〉,〈v₃,v₆〉,〈v₃,v₇〉}

图7－1　有向图

图中所有边都用无序偶对来表示,即图中每条边都是没有方向的。此时的图称为无向图。无向图的二元组表示可定义为如下形式。

G＝（V,R）

V＝{x｜x∈elemtype}

R＝{（x,y）｜x∈V,y∈V}

其中,（x,y）表示x和y之间的一条边,图7－2所示的是无向图,其顶点集和边集分别如下。

V＝{v₁,v₂,v₃,v₄,v₅,v₆,v₇}

R＝{（v₁,v₂）,（v₁,v₃）,（v₂,v₄）,（v₂,v₅）,（v₃,v₆）,（v₃,v₇）}

图7－2　无向图

7.1.2　基本术语

1.邻接点、相关边

如果（x,y）是无向图的一条边,则称x和y互为邻接点,称边（x,y）是顶点x和y的相关边。若〈x,y〉是有向图的一条边,则称顶点x邻接到顶点y,顶点y邻接于x,边〈x,y〉是顶点x,y的相关边,称为x的出边,y的入边。

图7－1中,边〈v₂,v₄〉是v₂和v₄的相关边,是v₂的出边,v₄的入边,v₂邻接到v₄,v₄邻接于v₂。

图7－2中,边（v₁,v₂）是v₁和v₂的相关边,v₁和v₂互为邻接点。

2.简单图

若图中不存在顶点到其自身的边,并且同一条边不重复出现,则称这样的图为简单图。

3.完全图

在一个有n个顶点的无向图中,若每个顶点到其他（n－1）个顶点都连有一条边,则图中有n×（n－1）/2条边,这样的图称为无向完全图,如图7－3所示。

在一个有n个顶点的有向图中,每两个顶点之间都存在着方向相反的两条边,则称此图为有向完全图,其边数为n×（n－1）,如图7－4所示。

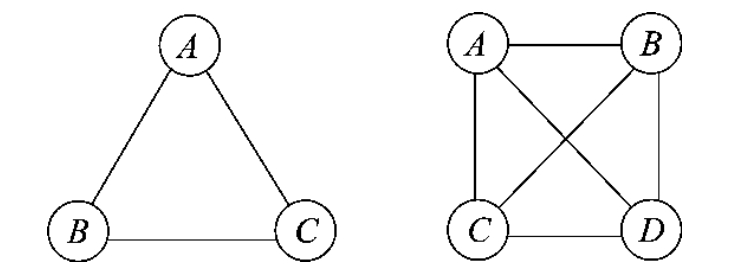
图7－3　无向完全图

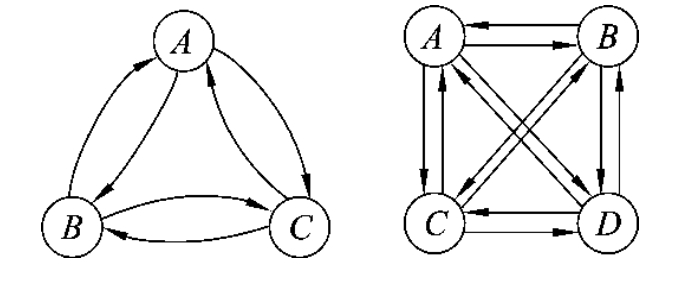
图7－4　有向完全图

4.稠密图、稀疏图

（1）稠密图:当一个图接近完全图时,则称它为稠密图。

（2）稀疏图:当一个图含有较少边数时,则称它为稀疏图。

5.顶点的度、入度、出度

顶点v的度是v的相关边的数目,计为TD（v）。有向图中顶点的度分为入度和出度,顶点v的入边的数目称为v的入度,记为ID（v）；顶点v的出边的数目称为v的出度,记为OD（v）；顶点v的度为TD（v）＝ID（v）＋OD（v）。

在图7－1所示的有向图中,顶点v₃的入度为1,出度为2,度为3。在图7－2所示的无向图中,顶点v₂的度为3。

若一个无向图中有n个顶点和e条边,则满足如下关系

若一个有向图中有n个顶点和e条边,则满足如下关系

6.路径、回路

图中从顶点v到顶点v′的路径是一个顶点序列v＝v₁,v₂,…,v_n＝v′,序列中任意相邻的两个顶点都存在一条边。如果是有向图,则其路径也是有向的。序列中顶点不重复的路径称为简单路径。路径长度是路径上的边的数目。

如果一条路径的第一个顶点和最后一个顶点相同,则该路径称为回路,除了第一个顶点和最后一个顶点,其余顶点不重复的回路,称为简单回路。

图7－5所示的无向图中,（1,2,4,1,3,4）是条路径,（1,2,4）、（1,3,4）、（1,3,4,1）都是简单路径,其中（1,3,4,1）是简单回路。

7.子图

假设有两个图G＝{V,R}和G′＝{V′,R′},如果V′是V的子集,E′是E的子集,则称G′是G的子图。图7－6所示的是无向图G₂的三个子图。

图7－5　无向图

图7－6　无向图G₂的若干个子图

8.连通图和连通分量

在无向图G中,如果从顶点v到顶点v′有路径,则称v和v′是连通的。如果图G中任意两个顶点之间都是连通的,则称G是连通图。若无向图是非连通图,则图中极大连通子图称为连通分量。连通分量具有以下4个特点。

（1）子图:连通分量是原图的子图。

（2）连通:连通分量是连通图。

（3）极大顶点数:连通子图再加入其他顶点就不连通了。

（4）极大边数:连通子图包含依附于这些顶点的所有边。

如图7－7所示,顶点A、B、C、D相互都是连通的,所以它是连通图。

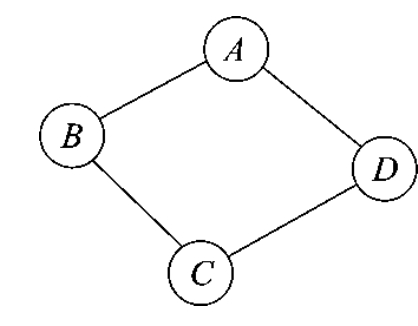
图7－7　连通图

而图7－8所示为非连通图及其连通分量。

9.强连通图和强连通分量

在有向图G中,如果对于每一对顶点v₁和v₂,既有从v₁到v₂,也有从v₂到v₁的路径,则称G是强连通图。有向图中的极大强连通子图也称为有向图G的强连通分量。强连通分量与连通分量的概念是相同的。

图7－9所示为强连通图；而图7－10所示为非强连通图,其强连通分量分别为子图{1,2,3,4},{5}和{6}。

图7－8　非连通图和连通分量

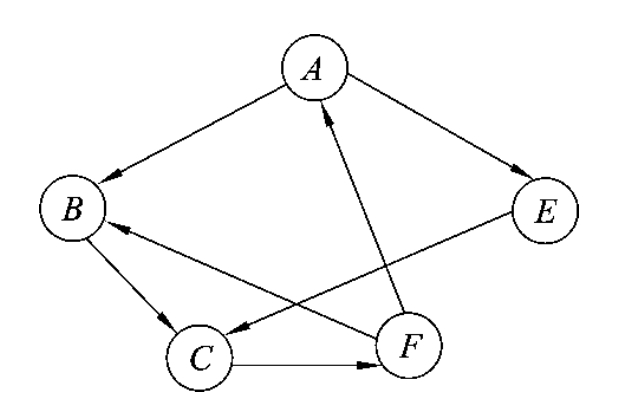
图7－9　强连通图

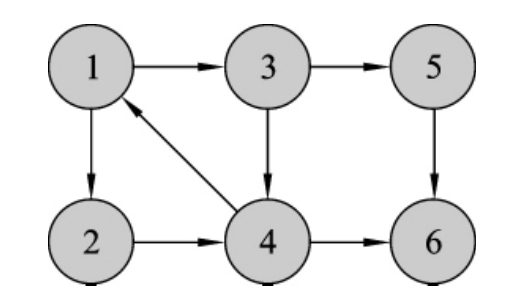
图7－10　非强连通图

10.生成树

一个图的生成树是包含图中所有顶点的极小（强）连通子图。生成树含有图中全部的n个顶点,但只能有n－1条边,顶点间都存在路径,但不存在回路。

图7－11　无向图及生成树

图7－11中,图（b）和图（c）,满足n个顶点n－1条边且连通的条件,它们都是图（a）的生成树。不过有n－1条边并不一定是生成树,如图（d）所示。

11.生成森林

在非连通图中,每个连通分量都对应一棵生成树,所有连通分量的生成树组成了非连通图的生成森林。

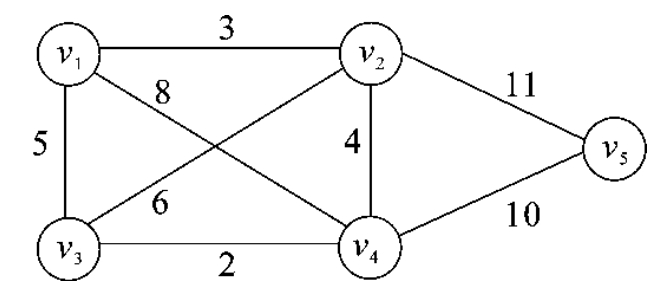
图7－12　无向网

12.权、网

在图的边或弧上,标有与它们相关的数,这种与图的边或弧相关的数称为权（weight）,它表示从一个顶点到另一个顶点的距离或代价。这种带权的图常称为网（network）。图7－12所示为无向网。

7.1.3　图的抽象数据类型描述

图的抽象数据类型的定义如下。

操作结果:从顶点v起深度优先遍历图G。

　　BFSTraverse(G,v,Visit());

操作结果:从顶点v起广度优先遍历图G。}ADTGraph