哈夫曼树及其应用

6.6　哈夫曼树及其应用

哈夫曼（Haffman）树是一种带权路径长度最小的二叉树,也称为最优二叉树,有着极为广泛的应用。

6.6.1　哈夫曼树的引入

1.常用术语

（1）路径长度　从树中的一个结点到另一个结点之间的分支构成两个结点间的路径,路径上的分支数目,称为路径长度。

（2）树的路径长度　从树根到每个结点的路径长度之和称为树的路径长度。

（3）结点的带权路径长度　从该结点到树根之间的路径长度与该结点上权的乘积。

（4）树的带权路径长度　树中所有叶子结点的带权路径长度之和,称为树的带权路径长度。

（5）最优二叉树　带权路径长度最小的二叉树,称为最优二叉树。

2.求树的带权路径长度

设二叉树具有n个带权值的叶结点,那么,从根结点到各个叶结点的路径长度与相应结点权值的乘积之和称为二叉树的带权路径长度（WPL）,记为如下形式。

其中:Wk为第k个叶结点的权值；L_k为第k个叶结点到根结点的路径长度。

【例6－11】　设给定权值分别为2,3,5,9的4个结点,如图6－34所示构造了5个形状不同的二叉树。试分别计算它们的带权路径长度。

图6－34　不同二叉树带权路径长度

图6－34中5棵树的带权路径长度分别如下。

（a）WPL＝2×2＋3×2＋5×2＋9×2＝38

（b）WPL＝2×3＋3×3＋5×2＋9×1＝34

（c）WPL＝2×2＋3×3＋5×3＋9×1＝37

（d）WPL＝9×3＋5×3＋3×2＋2×1＝50

（e）WPL＝2×1＋3×3＋5×3＋9×2＝44

5个图的叶结点具有相同权值,由于其构成的二叉树形态不同,则它们的带权路径长度也各不相同。其中,以图6－34（b）所示的带权路径长度最小,它的特点是权值越大的叶结点越靠近根结点,而权值越小的叶结点则远离根结点,事实上它就是一棵最优二叉树。由于构成最优二叉树的方法是由D.Haffman最早提出的,所以又称为哈夫曼树。

3.哈夫曼树的优点

在分析一些决策判定问题时,利用哈夫曼树可以获得最佳的决策算法。例如,要编制一个将百分制数（n）转换为五级分制的程序。这是一个十分简单的程序,只要用简单的条件选择语句即可完成。具体程序如下。

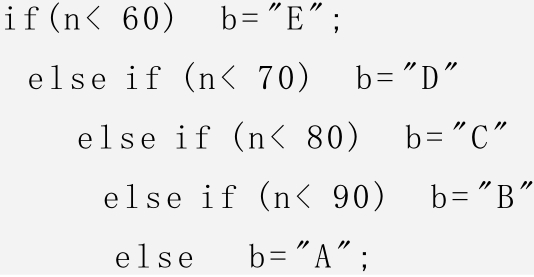
这一判定过程可以用图6－34（a）所示的判定树来表示。在管理信息系统中,判定树也称为决策树,是系统分析和程序设计的重要工具。

若这一程序需要反复使用且输入量又很大,则必须充分考虑程序的质量（即计算所花费的时间）问题。因为在实际考试中,学生的成绩在5个等级上的分布是不均匀的,设成绩分布规律及转换等级如表6－1所示。

表6－1　成绩分布规律及转换等级

对于这一成绩分布规律,如果用上面的程序来进行转换的话,则大部分的数据需进行三次或三次以上的比较才能得出结果。如果以百分比值5、15、40、30、10为权构造一棵由5个叶子结点构成的哈夫曼树,则可得到图6－35（b）所示的判定树,它使大部分数据经过较少的比较次数,就能得到换算结果。但是,由于每个判定框都有两次比较,将这两次比较分开,就可以得到如图6－35（c）所示的判定树,按此判定树编写出相应的程序,将大大减少比较的次数,从而提高运算的速度。

假设有10 000个输入数据,若按图6－35（a）所示的判定过程进行操作,则总共需进行31 500次比较；而若按图6－35（c）的判定过程进行操作,则总共仅需进行22 000次比较。

图6－35　百分制转换为五级分制的判定过程

6.6.2　哈夫曼树的建立

1.哈夫曼树构成的基本思想

（1）由给定的n个权值{W₁,W₂,…,W_n}构造n棵只有一个叶结点的二叉树,从而得到一个二叉树的集合F＝{T₁,T₂,…,T_n}。

（2）在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树,这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和。

（3）在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合F中。

（4）重复（2）（3）两步,直到F中只剩下一棵二叉树时,这棵二叉树便是所要建立的哈夫曼树。

下面以例6－11中的叶结点权值:2、3、5、9为例,介绍哈夫曼树的构造过程。

（1）取出权值最小的2和3,构成一棵二叉树,如图6－36（a）所示,其权值之和为5。

（2）再取出权值最小的5和5,构成一棵二叉树,如图6－36（b）所示,其权值之和为10。

（3）再取出权值最小的9和10,构成一棵二叉树,如图6－36（c）所示,其权值之和为19。

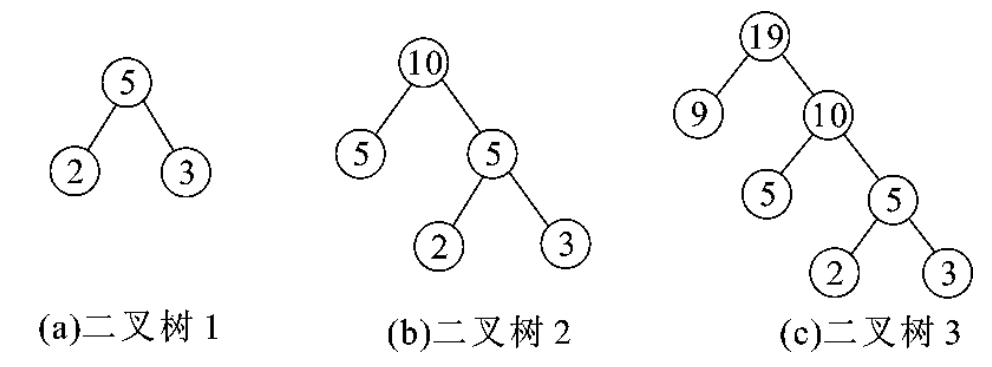
图6－36　哈夫曼树建立过程

图6－36（c）即为哈夫曼树,其带权路径长度为

WPL＝9×1＋5×2＋3×3＋2×3＝34

【例6－12】　设结点的权集W＝{10,12,4,7,5,18,2},建立一棵哈夫曼树,并求出其带权路径长度。

哈夫曼树的建立过程如图6－37所示。

（1）先按权值递增排列:2,4,5,7,10,12,18

取两个最小的权值构成二叉树如图6－37（a）所示。

（2）5,（6）,7, 10, 12, 18

再取5,6构成二叉树如图6－37（b）所示。

（3）7,10,（11）, 12, 18

再取7,10构成二叉树如图6－37（c）所示。

（4）（11）,12,（17）, 18

再取11,12构成二叉树如图6－37（d）所示。

（5）（17）,18,（23）

再取17,18构成二叉树如图6－37（e）所示。

（6）（23）,（35）

取最后两个权值23和35构成二叉树如图6－37（f）所示,即哈夫曼树。其带权路径长度计算如下。

WPL＝（18＋12）×2＋（10＋7＋5）×3＋（4＋2）×4＝150

图6－37　哈夫曼树的建立过程

2.哈夫曼树的构造算法

在构造哈夫曼树时,可以设置一个结构数组HFMT,用于保存哈夫曼树中各结点的信息。由二叉树的性质可知,具有n个叶结点的哈夫曼树共有2n－1个结点,所以2n－1即数组HFMT所需的存储空间,其结构体形式如下。

其中:weight域用于保存结点的权值；lchild和rchild域分别用于保存该结点的左、右孩子结点在数组HFMT中的下标；parent域用于判定一个结点是否已加入到要建立的哈夫曼树中。初始时parent的值为－1,当结点加入到树中时,该结点parent的值为其父结点在数组HFMT中的下标。

构造哈夫曼树时,首先将由n个字符形成的n个叶结点存放到数组HFMT的前n个分量中,然后根据哈夫曼方法的基本思想,不断将两个权值最小的子树合并为一个较大的子树,每次构成的新子树的根结点顺序放到HFMT数组中的前n个分量的后面。

6.6.3　哈夫曼编码

1.哈夫曼编码简介

在数据通信中,经常需要将传送的文字转换成由二进制字符0和1组成的二进制代码,称之为编码。

如果在编码时考虑字符出现的频率,让出现频率高的字符采用尽可能短的编码,出现频率低的字符采用稍长的编码,构造一种不等长编码,则电文的代码就可能更短。哈夫曼编码是一种用于构造使电文的编码总长最短的编码方案。

2.哈夫曼编码的方法

1）构造哈夫曼树

设需要编码的字符集合为{d₁,d₂,…,d_n},它们在电文中出现的次数集合为{w₁,w₂,…,w_n},以d₁,d₂,…,d_n作为叶结点,w₁,w₂,…,w_n作为它们的权值,构造一棵哈夫曼树。

【例6－13】　设有A、B、C、D、E、F六个数据项,其出现的频度分别为6、5、4、3、2、1,试构造一棵哈夫曼树,并确定它们的哈夫曼编码。

假设哈夫曼树按数据频度的权值从小到大,采用顺序存储结构存储。每次找到的权值最小值作为新生结点的左孩子结点,权值次最小值作为新生结点的右孩子结点,则左孩子结点的权值加右孩子结点权值之和为根结点的权值。按构造哈夫曼树的算法继续找权值最小的结点和次小的结点,如果有若干个最小权值相同的结点,则谁存储在前面的结点,谁就是当前找到的最小值。哈夫曼树构造过程如图6－38（a）所示。

图6－38　求哈夫曼编码

2）在哈夫曼树上求叶结点的编码

规定哈夫曼树中的左分支代表0,右分支代表1,则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该叶子结点对应字符的编码,如图6－38（b）所示,得到哈夫曼编码为:A＝10；B＝01；C＝00；D＝110；E＝1 111；F＝1 110。

在哈夫曼编码树中,树的带权路径长度的含义是各个字符的码长与其出现次数的乘积之和,也就是电文的代码总长。采用哈夫曼树构造的编码是一种能使电文代码总长为最短的不等长编码。

求哈夫曼编码的实质就是在已建立的哈夫曼树中,从叶结点开始,沿结点的双亲链域回退到根结点,每回退一步,就走过了哈夫曼树的一个分支,从而得到一位哈夫曼码值。由于一个字符的哈夫曼编码是从根结点到相应叶结点所经过的路径上各分支所组成的0、1序列,因此,先得到的分支代码为所求编码的低位码,后得到的分支代码为所求编码的高位码。

本章小结

1.树是一种以分支关系定义的层次结构,除根结点无直接前驱结点外,其余每个结点有且仅有一个直接前驱结点,但树中所有结点都可以有多个直接后继结点。树是一种具有一对多关系的非线性数据结构。

2.一棵非空的二叉树,每个结点至多只有两棵子树,分别称为左子树和右子树,并且左、右子树的次序不能任意交换。二叉树的左、右子树又分别都是二叉树。二叉树是本章的重点,必须重点掌握。

3.若所有分支结点都存在左子树和右子树,并且所有叶子结点都在同一层上,这样的一棵二叉树就是满二叉树。若除最后一层外,其余各层都是满的,并且最后一层或者为满,或者仅在右边缺少连续的若干个结点,则称此二叉树为完全二叉树。要求熟悉二叉树、满二叉树和完全二叉树之间的一些基本性质。

4.二叉树的遍历是指按某种顺序访问二叉树中的所有结点,使得每个结点都被访问且仅被访问一次。通过一次遍历,使二叉树中结点的非线性排列转为线性排列。要求熟练掌握二叉树的前序遍历、中序遍历、后序遍历及层次遍历的概念和算法。

5.二叉树具有顺序存储和链式存储两种存储结构。使用顺序存储时,必须按完全二叉树格式存储；使用二叉链式存储时,每个结点有两个指针域,具有n个结点的二叉树共有2n个指针,其中指向左、右孩子的指针有n－1个,空指针有n＋1个。

6.利用二叉树n＋1个空指针来指示某种遍历次序下的直接前驱结点和直接后继结点,这就是二叉树的线索化。

7.一般树的存储比较麻烦,但只要将一般树转换为二叉树存储就比较方便了。要求掌握一般树转换为二叉树的方法。

8.用二叉树表示图形数据结构时,如果去掉结点的指针项,则只按结点的中序序列存储,并给出这棵树的前序（或后序）“序表”；图形调入内存时,由中序的结点表及前序（或后序）“序表”来恢复二叉树,这是数据结构中的一种重要应用。

9.将算术表达式用二叉树来表示称为标识符树,也称为二叉表示树。利用标识符树的后序遍历可以得到算术表达式的后缀表达式,是二叉树的一种应用。

10.带权路径长度最小的二叉树称为哈夫曼树,要求能按给出的结点权值的集合,构造哈夫曼树,并求带权路径长度。在程序设计中,对于多分支的判别（各分支出现的频度不同）,利用哈夫曼树可以提高程序执行的效率,必须予以重点掌握。哈夫曼编码在通信中有着广泛的应用,应该有一定的了解。