测试的基础知识

10.1　测试的基础知识

10.1.1　测试

测试专业人员借助专门设备，通过实验方法对被检测的闸门取得数量观念的认识过程，称为测试。

测试结果可能表现为一定的数字、曲线，或某种图形、频率谱等。不论何种形式，其结果总包含一定的数值(大小或符号)以及相应的单位。

在测试过程中，不可避免地存在误差，在表示测试结果时，必须把测试结果的实际误差同时表示出来，以便掌握测试结果的可信赖程度。下面首先介绍误差分析中要用到的一些基础知识。

10.1.2　数理统计的一些基本概念

现将有关的数理统计基础理论与概率解释如下:

1.总体

数理统计把研究对象(为被测数据)的全体称为总体，或称为母体。

2.个体

个体是指总体中的每一个基本单元。

3.样本

从总体中抽取出来的部分个体，称为样本，或称为子样。

总体、个体、样本三者之间的关系就像图10-1所示的方格数那样，方格总数代表总体，以C表示;一个方格代表一个个体，以B表示;若干个方格组成一组代表样本，以A表示。一般情况下，总体包含的个体数目可以很多，甚至趋于无限多。因此，不可能把所有个体都加以研究，为了推断总体的性质，常从总体中抽取一部分个体进行研究，即通过研究样本的性质去推断总体的性质。

样本可分为“有意取样”和“随机取样”。在工程结构可靠度分析中，一般采用随机取样。随机取样又可分为单纯随机取样、系统随机取样以及分段、分层、分块或分群等随机取样，这可根据问题的实际情况而定。工程结构可靠度分析中，通常用单纯(或可能)随机取样，因此，常用抽签法或随机数表，以保证总体中每个个体有同等的被抽取机会。

4.样本的算术平均值

样本的算术平均值定义为:

式中:n——是样本中观测数据X_i的个数，称为样本的大小或子样的容量。

X_i——是样本中第i个试样的观测数据值。

图10-1　总体、个体、样本的关系

显然，样本算术平均值是反映数据的平均性质的。

5.样本方差

样本方差S²定义为:

它是各观测数据X_i与均值X之偏差的平方和除以样本的大小n减去1。因为所有偏差的和为零，即

所以n个偏差中只有(n－1)个是独立的。因此，我们就称它具有(n－1)个“自由度”。

方差S²的正平方根称为数据样本标准差，即

样本大小n越大，则样本的算术平均值X、标准差S就越接近于数据总体均值μ和数据总体标准差σ。在实际工程测试换算时，算术平均值与标准差的有效数字位数应比原测试值多1位。

6.变异系数

变异系数C_V定义为:

式中:S、分别为数据样本的标准差和算术平均值。

变异系数可作为一组样本数据相对分散程度的指标，常用百分数表示。它是无量纲数。

7.概率

概率是“随机事件”中使用的名词。在一定条件下，某事件A可能发生，也可能不发生，则事件A就称为随机事件。于是，我们进行的每一个试验结果都可以看成是一个随机事件。某事件的概率则是在一定条件下该随机事件发生的可能程度的大小。一般地，事件A的概率可记做P(A)。

概率有古典的定义和统计的定义。由于古典定义有很大的局限性，所以本书只介绍概率的统计定义。概率的统计定义是以大量的重复性实验和统计资料为基础的，故它与“频率”有关。

所谓“频率”是设事件A在n次随机试验中发生了m次，则其比值m/n叫做事件A发生的“频率”，记做f(A)=m/n。

当试验次数足够多时，就可以把频率f(A)作为事件A的概率的近似值。这就是概率统计定义的重要思想，如前所述记做P(A)。显然，任何随机事件的概率都是介于0和1之间的，即0≤P(A)≤1。但要强调的是，随机事件的频率与我们已进行的试验次数有关，而随机事件的概率都是完全客观地存在的，它反映了频率的稳定性。

8.样本的正态分布

样本的正态分布是一个极其重要的分布，人们对构件尺寸、疲劳寿命、材料的某些力学性能、测试的误差等数据进行了大量的统计分析。根据这些研究对象所作出的实验频率曲线如图10-2所示，大多具有如下几个特征:

(1) f(x)是单峰，对称的悬钟形曲线，对称轴在x=μ处。

(2)对于所有的x值，f(x)值大于零。

(3)曲线f(x)下方的总面积等于1，即f(x)d x= 1。

(4)x的取值范围是整个x轴，即－∞＜x＜+∞。

(5)在对称轴两边曲线上，各有一个拐点。

图10-2　样本正态分布图

能满足上述几个特征的数字表达式为:

式中:e= 2.78是自然对数的底;μ是总体的算术平均值;σ是总体标准差。

随机变量X具有上述特征的分布称为正态分布。在正态分布中，x≤x₀的概率等于图10-2中阴影部分的面积，即

9.总体参数的置信区间

某个物理量客观存在的量值——真值是不可知的，也是无法测得的。实验所得的测试值只是真值的近似反映，也即用估计值去近似，如数据总体平均值μ的估计就用样本算术平均值X来估计。但是，样本的算术平均值X不一定正好等于总体平均值μ，这就会带来较大的误差，而且误差的范围难以确定。为了弥补上述缺点，为总体参数的估计提供更多的信息，特提出了区间估计。

所谓区间估计，就是估计总体参数以某一概率包含在什么样的一个区间之中。此时，这个区间就称为总体参数的置信区间，而置信区间内包含数据总体参数的概率——置信概率，也称为置信度或置信水平，常以1－α表示，其中α称为显著性水平或显著度。

置信概率可表示为:

式中:(－kσ，kσ)为置信区间，k称为置信因子。

当样本n较大时，可用样本标准差S去近似总体标准差σ。当数据x服从正态分布时，若k= 1，则P(－σ≤σ)= 68.26%;

若k= 2，则P(－2σ≤2σ)= 95.44%;

若k= 3，则P(－3σ≤3σ)= 99.87%。

10.非参数检验

(1)χ²检验

现在来检验假设H:“X的分布函数F(x)为F₀(x)”，F₀(x)为某已知分布函数。

对X进行N次独立的观察得到观察值x₁，x₂，…，x_N，将样本观察值的范围R₁=(－∞，+∞)分成m个子区间(x_i－1，x_i)，其中－∞= x₀＜x₁＜…＜x_m=+∞，以v_i表示x₁，x₂，…，x_N落于(x_i－1，x_i)中的个数，即满足x_k∈(x_i－1，x_i)的k(≤N)个数，显然，= N。

另设H:“F(x)= F₀(x₀)”正确，令p_i= F₀(x_i)－F(x_i－1)＞0。

考虑统计量

η依赖于N及m，以下总固定m。注意如H正确，可由强大数定理→p_i(以概率1收敛)，当N甚大时，v_i≈Np_i。

皮尔逊定理:如H正确，则

是χ²(m－1)分布的密度函数。

由此定理可知，当N充分大时，可以认为η近似服从χ²(m－1)分布，对已给p＞0，可以由χ²分布表求得常数η_p，使

以子样值代入η后，如η＞η_p，则相对信度p/100而言，应否定H。实际中运用该定理时，通常取m为7～14。即子样容量N一般要取20以上，即要取大子样，否则结果不准。

例1以下是某大坝1号表孔弧形闸门各个部位的腐蚀测试数据。如表10-1所示。试根据测试数据来计算闸门的可靠度。

解:(1)支臂腹板厚度测试结果的可靠度

测量结果的可靠度分析方法为:首先画出支臂腹板厚度测试结果的直方图，然后计算其均值与方差，再利用χ²检验测试结果是否服从正态分布，最后确定其可靠度(或置信概率)为95%时支臂腹板厚度的置信区间。

①画出支臂腹板厚度测试结果的直方图

支臂腹板厚度的直方图见图10-3。

图10-3　支臂腹板厚度测试结果的直方图

表10-1　溢洪道1号弧门腐蚀测量表　单位:mm

②计算支臂腹板厚度的均值与标准差

支臂腹板厚度的均值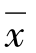与方差S²为

可见，μ== 19.6，σ= S^*= 0.18

③检验测试结果服从什么分布

假设H₀:x服从正态分布，x～N(19.6，0.18)

根据χ²分布检验，概率为

同理:P₂= 0.121 0，P₃= 0.186 4，P₄= 0.220 6，P₅= 0.186 4，P₆= 0.121 0，P₇= 0.056 1，χ²值计算过程如表10-2所示。

表10-2　χ²值计算过程

因此，接受假设H₀，表明支臂腹板厚度测量结果服从正态分布。

④确定其可靠度为95%时支臂腹板厚度的置信区间

当置信概率为95%时，

置信区间为

是标准正态分布关于的上侧分位数，当概率为1－α= 95%时，= 1.96

因此，支臂腹板厚度的可靠度为95%的概率时的置信区间为(19.7，19.5)。

(2)中主梁以下面板测试结果的可靠度

①中主梁以下面板厚度的直方图见图10-4。

图10-4　中主梁以下面板厚度测试结果的直方图

②确定其可靠度为95%时中主梁以下面板厚度的置信区间

当置信概率为95%时，

置信区间为

是标准正态分布关于的上侧分位数。当概率为1－α= 95%时，= 1.96。

因此，中主梁以下面板厚度的可靠度为95%的概率时的置信区间为(11.5，11.7)。(例毕)

(3)K-S检验

柯尔莫哥洛夫-斯米尔洛夫检验简称K-S检验，其基本思想是，用子样分布F_n(x)与总体(原假设)的理论分布F(x)作比较，来建立统计量D_n，进行检验。

设随机变量X的分布函数为F(x)，而且假定F(x)是x的连续函数。对X作几次独立观察得X₁，X₂，…，X_n，根据此子样作经验分布函数F_n(x)，由格里文科定理断定:

该定理表明:随机变量D_n=F_n(x)－F(x)= 1以概率1是无穷小(n→∞时)。下面的定理进一步说明:以概率1D是与

_n同级的无穷小。

柯尔莫哥洛夫定理:如函数是x的连续函数，则

K(y)的值有表可查。采用统计量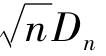后，可以像利用皮尔逊定理一样，利用柯尔莫哥洛夫定理来检验假定H:“X的分布函数为某个已知分布函数F(x)”，注意这里要求F(x)已知为连续函数。为此，只要对已给信度，由K(y)= 1－解出y= y即可;然后由_p上式，当n充分大时，可以认为:

以子样(X₁，X₂，…，X_n)代入D_n后，如果D_n＜y_p，则相对信度而言，可接受H;如D_n≥y_p，则否定H。

柯尔莫哥定理除可用做检验法外，还可用来估计未知发布函数F(x)。实际上，对已给信度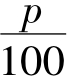，仿上取定y，由上式得知:当n充分_p大时，以近于1－的概率，有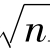D＜y;亦即对一切x∈R，有_np1

这说明，当n充分大时，以1－左右的概率，F(x)的图形，完全被包含在F_n(x)－与F_n(x)+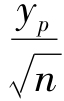所围成的区域内。这区域构成F(x)的置信区域，置信系数约为1－。K-S检验应取大子样，否则结果不够准确。但是在实际问题中，经验分布与理论分布应相当接近，即一般来说，D_n不应太大，因此，检验理论分布为给定的F(x)这一假定的否定域为:D_n＞D_n，p，p为给定的信度，临界值D_n，p由P{D_n＞D_n，p}= p确定。这一检验法称为柯尔莫哥洛夫检验。限于篇幅，这里不再举例说明。