泰森多边形

6.3.3　泰森多边形

泰森多边形(thiessen polygon)的另一个名称是弗若洛依多边形(Voronoi diagram)，是为了纪念荷兰气候学家泰森而命名的。其最早的应用是在降雨量的预测方面。为了从分布在某一地区的气象台站观测到的年降雨强度计算该地区的降雨量，泰森提出根据气象台站的分布来确定其影响大小(亦即权重)的方法，即:先将所有气象台站依据一定原则组成三角形，再作各边的垂直平分线，各平分线相交即构成若干个相邻的多边形(图6-20)，这些多边形的面积作为各台站降雨强度的权，按公式∑a_ip_i/∑a_i即可推算该地区的降雨强度。

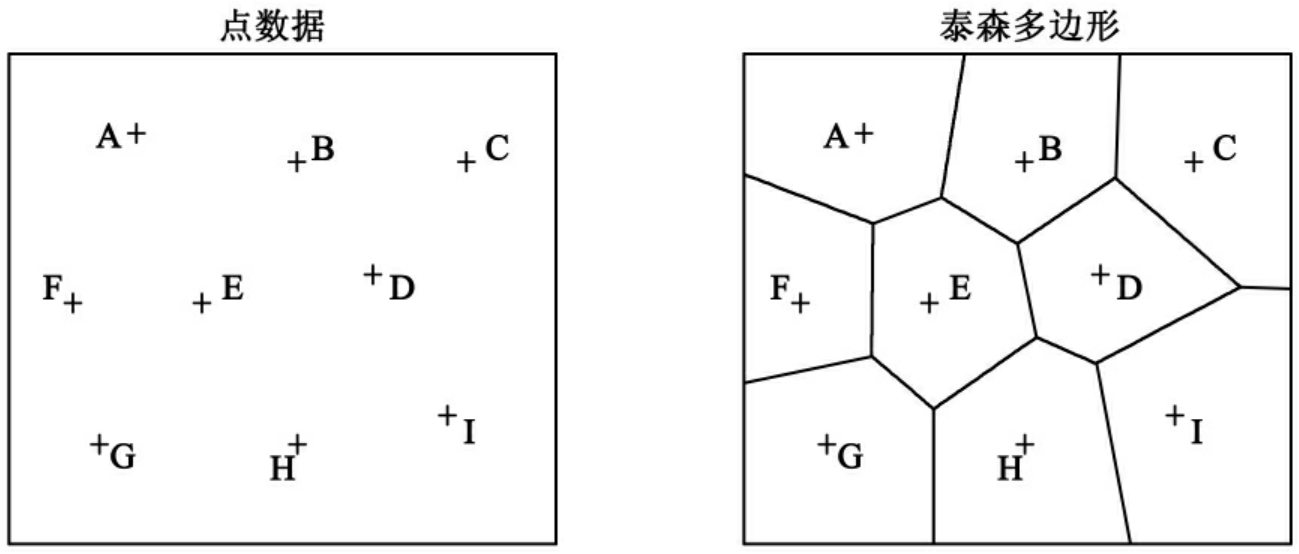
图6-20　泰森多边形的形成

泰森多边形的形成是基于这样一个假定:如果空间中的某一点没有观察值信息，那么最能描述该点状况的是离它最近的已知观察点。从图6-20中可以判断，一个已知观察点的泰森多边形内任何一点离此点的距离最近。从图中还可以看出，各已知点相连形成的是一个三角形网，该三角形网是泰森多边形的对偶图，它被称为笛劳利三角网(delaunay triangulation)。需指出的是，对于同样的一组离散点，构成三角形网的方法是多种多样的，这说明各点的泰森多边形不是唯一解。顺便指出，Delaunay三角网是模拟自然面或人工构成面的理想方法，在数字高程模型(DEM)中，它又被称为不规则三角网(TIN)。人们对Delaunay三角网的构建作了大量的研究，总结出诸多实用的算法，如三角形扩展法、二维点集三角剖分的动态生成与修改法、快速动态法等。

泰森多边形在城市研究中有较大的应用价值，如用于研究现有设施的负荷状况、多设施选址问题等。以下分别作简要介绍。

1.设施负荷分析

学校、医院等公共服务设施一般为其周围的居民服务，这些设施在现在和将来能否满足城市居民的要求是规划人员所关心的问题。评价设施的运转负荷可以用泰森多边形来完成初步的分析。下面以学校为例进行说明。

现假定评价小学的负荷状况，我们需要准确的小学分布图及城市土地利用、人口分布图。

第一步，确定各小学的位置。

第二步，构成小学的泰森多边形。

第三步，统计各泰森多边形内人口状况。理想的方法是能够获取多边形内各栋住房的居民结构，经简单的累加即可得到各区人口的数量及年龄结构。由于目前不可能有如此详细的信息，只能从住房的结构及数量上作简要的估计，得出现在和将来小学生的数量。

第四步，分别将各小学的规划容量与其实际需求作对比，即可获得该学校是否满足要求的定量信息。

其他设施负荷的评定过程与此大致类似，只是数据源的要求有些不同。但需指明，城市中道路、建筑物等的空间分布是不规则的，不能保证各个方向都通畅无阻，因此用泰森多边形来确定的服务范围并不能完全反映客观实际，这也是前面提出的“初步分析”的原因。而如果设施的服务不受空间地物的阻隔所限制，那么泰森多边形的应用将更为人们所接受。传呼台就是这样一类设施，除高大建筑物的阻挡外，由它发射的电磁波基本均匀地覆盖其周围一定范围的区域。所以，将传呼台构成的泰森多边形与其实际功率所覆盖的空间范围进行对比，可以评价城市各地接受到的移动通讯的服务水平。

2.设施选址

设施选址是综合应用定性、定量、定位方法的典型代表，国外学者很早就对这一问题展开了研究。由于新技术(如计算机技术)的应用及认识上的一步步深化，选址问题已有一些比较成熟的算法。早期的研究一般是将用户(或需求)离散化，成为空间上的一系列需求点;而连续二维表面上以用户的分布函数为基础的选址研究尚处于探索阶段。

设施选址可分为单设施选址和多设施选址两类。对于单设施选址，情况较为简单，只要先确定一定的区域范围，如在某一行政街区内建设一所中学，再以已有离散化的用户需求点为依据，求其距离总和最小的点位，该点位就是设施的地点，这种运算需要一个优化的过程，优的算法也比较关键。多设施选址中由于要顾及所有设施，使其总体布局最优化，因而要应用运筹学中的最优算法，比如线性规划法。多设施选址的一般数学模型为:

ABC f(f₁，f₂，…，f_m，u₁，u₂，…，u_n)

其中:函数f为设施点和用户点的费用函数。A、B、C为选址准则，A表示优化的动作(最大或最小);B表示优化的设施对象(最大、最小表示考虑个别设施、总和表示全局考虑);C表示优化的用户对象(它决定了是以全体用户为基础进行优化，还是只以部分用户为基础给予优化)。

以上的数字模型可形成多种选址准则(共18种)，而以下三类是经常遇到的:

第一类准则称为“总和最小化”(minisum)准则。它的直观解释是使所有用户距待定址设施的距离总和达到最小，这样的结果是使用户总的出行量达到最低，从而最大限度地达到方便用户的目的。学校、商场、医院、邮局等类型的公共设施要应用这类准则进行选址。

实际运算时先根据具体情况划分用户区，利用单设施选址算法求得各区内最优设施点;以各区的最优点为基础构成泰森多边形，重新计算各多边形内的距离点乃至整个区域的距离总和;将泰森多边形作为新的用户分区，继续以上求解过程，得出各区新的设施点。直至最终用户区不再变化时，各设施的点位即为最佳位置。

求解的过程比上述的描述要复杂得多，这里只给出该问题的目标函数模型:

设S为二维平面R²上的一个有界封闭区域，该区域确定了空间计算的范围。P={x₁，…，x_m}为该区域内m个设施点。Φ(x)为用户密度函数，可理解为用户分布密度，它是一个连续函数。VD={V₁，…，V_m}是m点集P且以区域S为边界构成的泰森多边形(VD图)。各用户点x到设施点x_i的几何距离记为|x－x_i|，费用函数为f(|x－x_i|)。那么目标函数记为:

优化的数学模型为:

Mini F(x₁，…，x_m)其中，x_i∈S i=1，…，m

第二类准则称为“最大最小化”(minimax)，也就是要使设施点到其服务范围最远处的用户距离达到最小，以便给用户提供及时服务。这类准则可运用于那些非经常性提供紧急服务的公共设施，如公安局、消防站等。

以消防站为例。每个消防站都有其“反应范围”，即某一规定的时间(如10分钟)所能到达的区域，超过这个范围，将不能保证在规定的时间内到达。选址问题是使各消防站都能满足这一要求，或者说，在现实状况中尽量满足这一需求。

运算中以某种方法先形成初始的设施位置，计算各位置形成的泰森多边形内与最远距离用户的距离值，如果所有设施点都满足给定的距离要求，那么可得到设施点的优化布局。

第三类准则称为“最小最大化”(maxmini)，也就是尽量使设施远离用户区。这种准则应用于那些“不受欢迎”的设施类别，如污染工厂、火葬场、传染病医院、煤气站、易燃易爆品仓库、垃圾处理厂等。这些设施对环境有较大的影响，有些则是对周围环境有较大的敏感性。

这一准则主要是看设施点与最近用户间的距离是否大于某一规定的标准。如果研究区域内有这类地区，则可将设施置于该地区内;如果没有符合的地区点位，则意味着需采取必要的隔离措施。不管是否要采取隔离措施，仍然有必要找到较为合理的点位——如果没有最理想点位。

这一问题最终仍归结于寻找一些泰森多边形区域，不同的是此时最佳的选址点已经不再是泰森多边形的中心，而是靠近整个区域边界的某些泰森多边形顶点上。由泰森多边形的性质可知，这些多边形的顶点是距其中心(用户点)最远的点，因而是此类设施的最佳位置。

以上所提供的几类设施选址问题已进行了多年的研究，而其中最优解的算法则处于不断发展之中。泰森多边形的应用也将随着研究的不断深化而得到深化。需再次指出，泰森多边形是解决问题诸多环节上的一环，与相关的方法联合使用能使其发挥最大的效益。

缓冲区、扩展、泰森多边形与接近度并无概念上的隶属关系，这里将它们集中在一起介绍，是由于它们都能实现空间实体间距离关系的量度，体现了接近度的特色。这是一种划分方法，重要的是对这三类功能本身的概念及应用要有十分清晰的了解。