(1/5) 函数项级数的概念
(1)函数项级数定义 如果 是定义在某个区间
是定义在某个区间![]() 上的函数,则称函数
上的函数,则称函数  为区间
为区间![]() 上的函数项无穷级数,简称为函数项级数。 (2)函数项级数与常数项级数关系 对于每个确定的值
上的函数项无穷级数,简称为函数项级数。 (2)函数项级数与常数项级数关系 对于每个确定的值![]() ,函数项级数就变为常数项级数
,函数项级数就变为常数项级数 
 (3)函数项级数和函数 在收敛域上,函数项级数的和是
(3)函数项级数和函数 在收敛域上,函数项级数的和是![]() 的函数
的函数 ,通常称
,通常称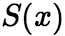 为函数项级数的和函数,这个函数的定义域就是级数的收敛域,并写成
为函数项级数的和函数,这个函数的定义域就是级数的收敛域,并写成  在收敛域上,部分和满足
在收敛域上,部分和满足 。
。
(2/5) 幂函数及其收敛性
1)幂级数定义: 形如
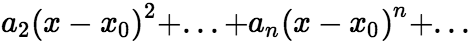 的级数称为
的级数称为 的幂级数,其中
的幂级数,其中 均为常数,称为幂级数的系数。 当
均为常数,称为幂级数的系数。 当 时,级数
时,级数 称为
称为![]() 的幂级数 (2)幂级数收敛性判断: 对于形如
的幂级数 (2)幂级数收敛性判断: 对于形如 的幂级数 若设
的幂级数 若设 ,则
,则 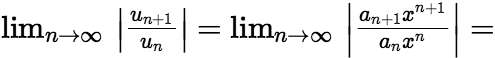
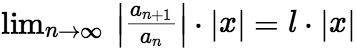 根据任意项级数判别法可知: (i)当
根据任意项级数判别法可知: (i)当 时, 若
时, 若 ,即
,即 ,该幂级数绝对收敛; 若
,该幂级数绝对收敛; 若 ,即
,即 ,该幂级数发散; 若
,该幂级数发散; 若 ,即
,即 ,则比值判别法失效,该幂级数可能收敛也可能发散。 (ii)当
,则比值判别法失效,该幂级数可能收敛也可能发散。 (ii)当 ,由于
,由于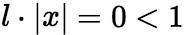 ,该幂级数对任何
,该幂级数对任何![]() 都收敛,此时定义
都收敛,此时定义 . (3)幂级数的收敛半径、收敛区间、收敛域 (i)定义:对任意一个幂级数
. (3)幂级数的收敛半径、收敛区间、收敛域 (i)定义:对任意一个幂级数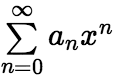 ,都存在一个
,都存在一个![]() ,
,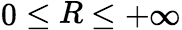 ,使对一切
,使对一切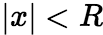 都有级数
都有级数 绝对收敛,而当
绝对收敛,而当 时级数发散。称
时级数发散。称![]() 为该幂级数的收敛半径,
为该幂级数的收敛半径, 为收敛区间。 当幂级数只在
为收敛区间。 当幂级数只在![]() 一点收敛时,
一点收敛时,![]() ;当对一切
;当对一切![]() 幂级数都收敛时
幂级数都收敛时 。 再由幂级数在
。 再由幂级数在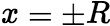 的收敛性就可以决定它的收敛域是
的收敛性就可以决定它的收敛域是


 这四个区间之一。 (ii)收敛半径求法: 对任意一个幂级数
这四个区间之一。 (ii)收敛半径求法: 对任意一个幂级数 ,若
,若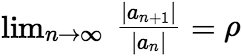 ,则当
,则当![]() 为非零正数时,收敛半径
为非零正数时,收敛半径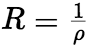 ;当
;当![]() 时,收敛半径
时,收敛半径 ;当
;当 时,收敛半径
时,收敛半径![]() 。
。
(3/5) 阿贝尔定理
如果幂级数 当
当 时收敛,则适合不等式
时收敛,则适合不等式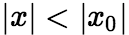 的一切
的一切![]() 使幂级数绝对收敛。反之,如果级数
使幂级数绝对收敛。反之,如果级数 当
当 时发散,则适合不等式
时发散,则适合不等式 的一切
的一切![]() 使这幂级数发散。 推论:如果幂级数
使这幂级数发散。 推论:如果幂级数 不是仅在
不是仅在![]() 一点收敛,也不是在整个数轴上都收敛,则必有一个确定的正数
一点收敛,也不是在整个数轴上都收敛,则必有一个确定的正数![]() 存在,使得 若
存在,使得 若 ,该幂级数绝对收敛; 若
,该幂级数绝对收敛; 若 ,该幂级数发散; 若
,该幂级数发散; 若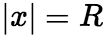 ,该幂级数可能收敛也可能发散。
,该幂级数可能收敛也可能发散。
(4/5) 幂级数的性质
设幂级数 与
与 的收敛半径分别是
的收敛半径分别是 与
与 (
(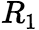 与
与 均不为0),它们的和函数分别为
均不为0),它们的和函数分别为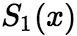 与
与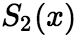 (1)(加法与减法运算)
(1)(加法与减法运算) 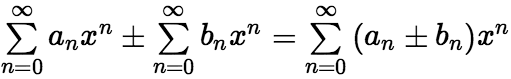
 所得的幂级数
所得的幂级数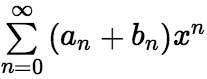 仍收敛,且收敛半径是
仍收敛,且收敛半径是 与
与 中较小的一个。 (2)(乘法运算)
中较小的一个。 (2)(乘法运算) 


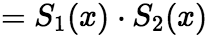 两幂级数相乘所得的幂级数仍收敛,且收敛半径是
两幂级数相乘所得的幂级数仍收敛,且收敛半径是 与
与 中较小的一个。 (3)(微分运算) 若幂级数
中较小的一个。 (3)(微分运算) 若幂级数 的收敛半径
的收敛半径![]() ,则在
,则在 内和函数
内和函数![]() 可导,且有
可导,且有 
 且求导后所得的幂级数的收敛半径仍为R。 (4)(积分运算) 若幂级数
且求导后所得的幂级数的收敛半径仍为R。 (4)(积分运算) 若幂级数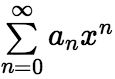 的收敛半径R,则和函数
的收敛半径R,则和函数![]() 在该区间内可积,且有
在该区间内可积,且有 
 且求导后所得的幂级数仍收敛,且收敛半径仍为R。
且求导后所得的幂级数仍收敛,且收敛半径仍为R。
(5/5) 函数展成幂级数
若找到一个幂级数,保证在某区域内收敛,且其和恰好就是给定的函数![]() ,则称函数
,则称函数![]() 在该区间内能够展开成幂级数。 (1)函数展开成泰勒级数或麦克劳林级数
在该区间内能够展开成幂级数。 (1)函数展开成泰勒级数或麦克劳林级数  在点
在点![]() 附近有任意阶导数,称幂级数
附近有任意阶导数,称幂级数 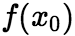 +
+ +
+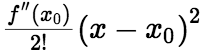 +
+
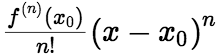
 为
为![]() 在点
在点![]() 处的泰勒级数,并称
处的泰勒级数,并称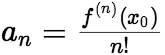 (
( )为
)为![]() 在点
在点![]() 处的泰勒系数,特别地,当
处的泰勒系数,特别地,当 时,称幂级数
时,称幂级数 ![]() +
+![]() +
+![]() +
+

 为
为![]() 的麦克劳林级数,并称
的麦克劳林级数,并称 为
为![]() 的麦克劳林系数。 (2)函数展开成泰勒级数的充分必要条件: 设函数
的麦克劳林系数。 (2)函数展开成泰勒级数的充分必要条件: 设函数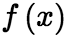 在点
在点![]() 的某一邻域
的某一邻域![]() 内具有各阶导数,则
内具有各阶导数,则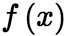 在该邻域内能展开成泰勒级数的充分必要条件是在该邻域内
在该邻域内能展开成泰勒级数的充分必要条件是在该邻域内 的泰勒公式中的余项
的泰勒公式中的余项 当
当 时的极限为零,即
时的极限为零,即  (3)几个常见的麦克劳林展开式
(3)几个常见的麦克劳林展开式 
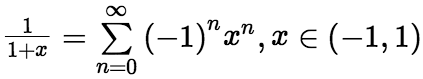





 (4)求函数幂级数展开式的方法: (i)直接展开法 求各阶导数,代入泰勒级数并检查泰勒余项
(4)求函数幂级数展开式的方法: (i)直接展开法 求各阶导数,代入泰勒级数并检查泰勒余项 的区间。 (ii)间接展开法 利用函数与已知幂级数展开式的函数之间关系及其在收敛区间的性质求得。
的区间。 (ii)间接展开法 利用函数与已知幂级数展开式的函数之间关系及其在收敛区间的性质求得。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















