(1/3) 多元复合函数的求导法则
(1)多元函数与一元函数的复合 如果函数 及
及 都在点
都在点 可导,函数
可导,函数 在对应点
在对应点![]() 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数 在点
在点 可导,且有
可导,且有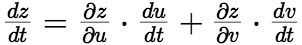 . (2)复合函数的中间变量均为多元函数的情形 如果函数
. (2)复合函数的中间变量均为多元函数的情形 如果函数 都在点
都在点![]() 具有对
具有对![]() 及
及![]() 的偏导数,函数
的偏导数,函数 在对应点
在对应点![]() 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数 在点
在点![]() 的两个偏导数存在,且有
的两个偏导数存在,且有  ,
,  . 推广:设
. 推广:设 则
则  ,
,  . 注:设
. 注:设 ,我们常用
,我们常用 表示
表示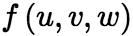 对第一个变量u的偏导数,类似的有
对第一个变量u的偏导数,类似的有 ,
, ,
,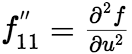 ,
,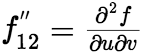 ,
,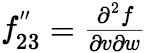 等等。 (3)复合函数的中间变量既有一元函数又有多元函数的情形 如果函数
等等。 (3)复合函数的中间变量既有一元函数又有多元函数的情形 如果函数 在点
在点![]() 具有对
具有对![]() 及对
及对![]() 的偏导数,函数
的偏导数,函数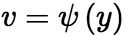 在点
在点![]() 可导,函数
可导,函数 在对应点
在对应点![]() 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数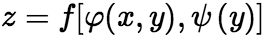 在点
在点![]() 的两个偏导数存在,且有
的两个偏导数存在,且有 ,
, 。
。
(2/3) 全微分的形式不变性
设 具有连续偏导数,则有全微分
具有连续偏导数,则有全微分 . 如果
. 如果 具有连续偏导数,而
具有连续偏导数,而 也具有连续偏导数,则
也具有连续偏导数,则  =
= =
=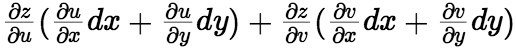 =
= . 由此可见,无论
. 由此可见,无论 是自变量或中间变量
是自变量或中间变量 的函数,函数
的函数,函数 它的全微分形式是一样的.这个性质叫做全微分形式不变性. 注:在求多元隐函数的偏导数或全微分时,一阶全微分形式不变性是重要工具。
它的全微分形式是一样的.这个性质叫做全微分形式不变性. 注:在求多元隐函数的偏导数或全微分时,一阶全微分形式不变性是重要工具。
(3/3) 隐函数的求导法则
(1)由方程式确定的隐函数的求导法 (i)由一个方程式确定的一元隐函数求导法 设函数 在点
在点 的某一邻域内具有连续偏导数,
的某一邻域内具有连续偏导数,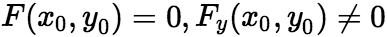 ,则方程
,则方程 在点
在点 的某一邻域内恒能唯一确定一个连续且具有连续导数的函数
的某一邻域内恒能唯一确定一个连续且具有连续导数的函数 ,它满足条件
,它满足条件 ,并有
,并有 . 求导公式证明:将
. 求导公式证明:将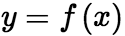 代入
代入 ,得恒等式F(x,f(x))=0, 等式两边对x求导得
,得恒等式F(x,f(x))=0, 等式两边对x求导得 , 由于
, 由于 连续,且
连续,且 ,所以存在
,所以存在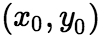 的一个邻域,在这个邻域内
的一个邻域,在这个邻域内 ,于是得
,于是得 ,
, (ii)由一个方程式确定的二元隐函数求导法 设函数
(ii)由一个方程式确定的二元隐函数求导法 设函数 在点
在点 的某一邻域内具有连续的偏导数,且
的某一邻域内具有连续的偏导数,且 ,则方程
,则方程 在点
在点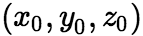 的某一邻域内恒能唯一确定一个连续且具有连续偏导数的函数
的某一邻域内恒能唯一确定一个连续且具有连续偏导数的函数 ,它满足条件
,它满足条件 ,并有
,并有  ,
, . 注:公式的证明:将
. 注:公式的证明:将 代入
代入 ,得
,得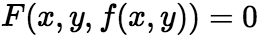 , 将上式两端分别对
, 将上式两端分别对![]() 和
和![]() 求导,得
求导,得 ,
,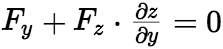 . 因为
. 因为![]() 连续且
连续且 ,所以存在点
,所以存在点 的一个邻域,使
的一个邻域,使 于是得,
于是得, (2)由方程组确定的隐函数的求导法 (i)由方程组确定的一元隐函数求导法 设有3个变量2个方程构成的方程组
(2)由方程组确定的隐函数的求导法 (i)由方程组确定的一元隐函数求导法 设有3个变量2个方程构成的方程组 其中
其中![]() 有连续偏导数,若在区间
有连续偏导数,若在区间![]() 上存在函数组
上存在函数组 满足该方程组,则说该方程组确定了隐函数
满足该方程组,则说该方程组确定了隐函数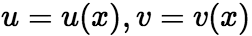 。若它们可导并求
。若它们可导并求 与
与 ,则由
,则由 两边分别对
两边分别对![]() 求导,应用复合函数求导法则可得
求导,应用复合函数求导法则可得  这可看成是以
这可看成是以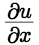 、
、 为未知量的二元一次方程组,可利用克莱姆法则求出
为未知量的二元一次方程组,可利用克莱姆法则求出 与
与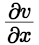 。 (ii)由方程组确定的二元隐函数求导法 设有4个变量2个方程构成的方程组
。 (ii)由方程组确定的二元隐函数求导法 设有4个变量2个方程构成的方程组 确定隐函数
确定隐函数 其中
其中![]() 有连续偏导数,则 偏导数
有连续偏导数,则 偏导数 ,
, 由方程组
由方程组 确定; 偏导数
确定; 偏导数 ,
, 由方程组
由方程组 确定.
确定.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















