隐函数微分法

§6.3　隐函数微分法

隐函数可分为由单个方程确定的隐函数以及由隐函数组确定的隐函数，隐函数可以是一元的，也可以是多元的。对这部分内容，我们首先要掌握隐函数的存在唯一性定理，然后再熟悉隐函数求导的公式和程序。而隐函数（组）的存在唯一性定理，一般数学分析教材上都有，在此不再罗列。

一、单个方程确定的隐函数偏导数的求法

我们以隐函数

为代表作分析。

1．公式法

若F对各个变量皆存在连续的一阶偏导数，且F′_z≠0，则由F（x，y，z）＝0确定的隐函数z＝z（x，y）也是连续可偏导的，并且有公式

2．链式法则的应用

在方程F（x，y，z）＝0中，视z＝z（x，y），即

上述（3）式的两边分别对x，y求偏导数：

立得（2）式。

3．全微分法

一阶全微分具有形式不变性的优点，可广泛应用于求隐函数的微分以及各个偏导数，且不易出错，希望读者能掌握其精髓。现对方程（1）的两边求微分：

只要F′_zdz≠0，立得

据此仍有（2）式成立。

解一　（公式法）取。

视x，y，z为三个独立变量求偏导数，代入公式（2）可得

解二　原方程改写为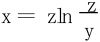，两边对x求偏导：

两边对y偏导，视z＝z（x，y），

整理得　以下同解法一。

解三　全微分法对两边求微分：

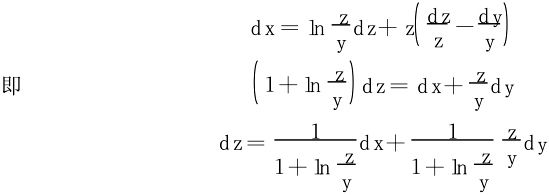
下面举例说明单个方程确定的隐函数的二阶偏导数的求解方法。

例2　设z＝z（x，y）由方程z⁵－xz⁴＋yz³＝1确定，求。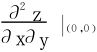

解　在原方程两边对x，y求偏导，分别得到：

以x＝y＝0代入原方程得z＝1，再以x＝y＝0，z＝1代入以上的两个偏导数方程（6），（7）得出

然后对（6）式两边关于y再求偏导，得到：

以x＝y＝0，z＝1代入（8）式，得到

注　隐函数的二阶偏导数一般不是直接对一阶偏导数再求一次偏导数，而是对方程直接求两次偏导运算，而且特殊值的代入时机亦须准确把握。

例3　已知z＝z（x，y）由x²＋y²＋h²（z）＝1确定，且h（z）具有所需的性质，求。

（北京师范大学2003年）

解　原方程两边对x求偏导

解出　

由x，y的对称性类似得

对（9）式两边再关于y求偏导

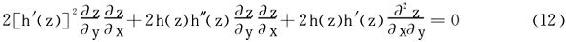
将（10）、（11）代入（12）解得

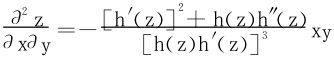
二、隐函数组微分法

对于多变量多个方程确定的隐函数偏导数的求法，亦如单个方程的情形，有公式法、利用复合函数偏导数的链式法以及全微分的方法。

1．公式法

以四个变量两个方程的隐函数组说明。

满足

（1）F（x₀，y₀，u₀，v₀）＝0，G（x₀，y₀，u₀，v₀）＝0　（初始条件）；

（2）在P₀（x₀，y₀，u₀，v₀）的某邻域内，函数F，G以及它们各个偏导数皆连续；

（3）在点P₀不等于零。

则在点P₀的某邻域内，由方程组（13）唯一地确定了两个二元隐函数

u＝u（x，y），v＝v（x，y）

并且u（x，y），v（x，y）连续可偏导，求导公式是

2．复合函数链式法则的应用

在推导公式（14）时，使用的就是对方程组（13）的两边关于x，y分别求偏导数的方法，视u和v为x，y的函数。

依据线性方程组的克兰姆法则立得（14），我们在解题时只要掌握了其中的数学思想，就不必去死记硬背某些公式，这样在减轻负担的同时反而提高了学习效率。

3．全微分法

对方程组（13）的两边求微分，利用微分的形式不变性，立得关于dx，dy，du，dv的方程

当时，可得唯一解du，dv，从而一步到位地获得，这是一种单纯的不易出错并且勿需记忆的方法，希望各位读者悉心掌握。

例4　求方程组所确定隐函数u（x，y），v（x，y）的偏导数。

（天津大学）

解一　原方程组两边关于x求偏导，得

解得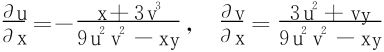　

解二　原方程组两边求微分并移项

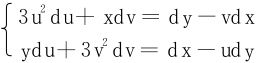
同时解得　

可同时算得四个偏导数。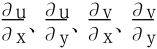

例5　设函数u（x）是由方程组所确定，且。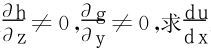

（清华大学）

分析　方程组含三个方程，四个变量x、y、z、u，故应该有一个是自由变量。通过直观判断或由雅可比行列式不能为0分析，可选取x作为自变量，y、z、u皆是x的一元函数，这样，求导数或是求偏导数时才不致出错。

解一　对　　两边关于x求导数，视y＝y（x），z＝z（x），得

解出　

于是　

解二　原方程组求全微分

从第3式解出代入第2式得出

再代入第1式：

一样得出结论。

将两种解法做一个比较，不难看出，利用全微分方法简便易行，仿佛用自动傻瓜相机拍照一般，会按快门即行。

最后说一下反函数组及坐标变换，以三维为例。设有坐标变换

假若变换式（15）的雅可比行列式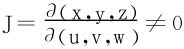，那么变换T就有唯一的逆变换

反函数组的微分法是一般隐函数组微分法的特例，不再赘述。在此只须陈述关于坐标变换雅可比行列式的一个非常有用的性质：

公式（17）告诉我们，不必求得逆变换（16），我们亦可以轻松地通过原变换的雅可比行列式算得逆变换的雅可比行列式：

这一性质在计算重积分时经常使用，谨记！

习题6.3

1．设。

（上海交大）

（西北电讯）

3．设方程组。

（北京大学）

4．设y＝y（x），z＝z（x）由方程。

（99数学（一））

5．设u＝xy²z³，若z＝z（x，y）由方程x²＋y²＋z²＝3xyz确定，求。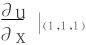

6．由e^z－xyz＝0确定z＝z（x，y），求。

7．。

8．z³－3xyz＝a³，求。

（北京科技大学98年）

9．z＝z（x，y）是F（xyz，x²＋y²＋z²）＝0所确定的可微隐函数，试求gradz。

（华师大2000年）

10．设f可微，u＝f（x²＋y²＋z²），方程3x＋2y²＋z³＝6xyz

　（1）确立了z＝z（x，y），求；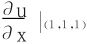

　（2）确立了y＝y（x，z），求。

（中科大）