一个简单的一维例子

15.4.2 一个简单的一维例子

我们在前面已经提到过，卡尔曼滤波器中的FORWARD算子将一个高斯分布映射成另一个新的高斯分布。这被转变成一个根据原有的均值与协方差矩阵计算新的均值与协方差矩阵的过程。要得到一般（多元）情况下的更新规则需要相当多的线性代数知识，因此我们暂时只讨论一种非常简单的一元情况；后面我们会给出一般情况下的结论。甚至对于一元情况，计算也是非常繁冗的，但是我们认为值得看一看这里的计算过程，因为卡尔曼滤波器的有效性与高斯分布的数学特性的关系实在太密切了。

我们将考虑的时序模型描述了有噪声观察Zt的单一连续状态变量Xt的随机行走。一个可能的例子是“消费者信心”指数，可以为它建立模型，每个月发生一次随机的高斯分布变化，同时通过一个随机的消费调查来度量——这个调查也会引入一个高斯采样噪声。假设其先验分布为具有方差的高斯分布：

（为了简化，我们使用同样的符号α 来表示本节所有的归一化常数。）转移模型只是简单地在当前状态中增加了一个具有常数方差的高斯扰动：

然后假设传感器模型具有方差为的高斯噪声：

现在，已知先验分布P(X0)，我们可以使用公式(15.15)计算单步预测分布：

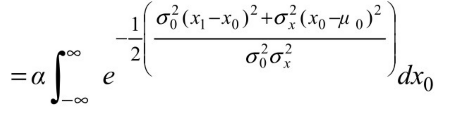
这个积分看来相当复杂。取得进展的一个关键之处在于要注意到指数部分是两个 x0的二次表达式的和，因此仍然是 x0的二次多项式。一个非常简单的技巧，大家熟知的配方法，允许将任何二次多项式+bx0+c改写为平方项与独立于x0的余项之和。余项部分可以从积分中移出，我们得到：

现在这个公式中的积分部分就是一个全区间上的高斯分布积分，也就是 1。因此，只给我们留下了二次多项式中的余项。

第二个关键的步骤在于要注意到这个余项一定是关于x1的二次多项式；事实上，经过化简以后，我们得到：

也就是说，这个单步预测分布是一个具有相同均值μ0的高斯分布，而其方差则等于原来方差与转移方差的和。直觉的短暂经验显示出直观上这应该是合理的。

为了完成更新步骤，我们还需要对第1个时间步的观察即z1进行条件化。根据公式(15.16)，这可由下式给出：

P(x1z1)=α P(z1|x1)P(x1)

我们再一次合并指数，并对指数进行配方（习题15.6），得到

于是，经过一次更新循环，我们得到了状态变量的一个新的高斯分布。

根据公式（15.17）的高斯表达式，我们发现，新的均值和标准差可以按照下面的公式由原来的均值和标准差计算得到：

图15.8显示了对转移模型和传感器模型的特定取值的一个更新周期。

图15.8 对随机行走进行卡尔曼滤波器更新的一个周期内的各阶段，由均值μ0=0.0，标准差σ0=1.0给定先验概率分布，由σx=2.0给定转移噪声，由σz=1.0给定传感器噪声，第一个观察值是z1=2.5（在x轴上标出）。注意相对于P(x0)，预测P(x1)是如何被转移噪声拉平的。还要注意到后验分布P(x1|z1)的均值比观察值z1略偏左，因为这个均值是预测与观察结果的加权平均

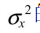前面一对公式扮演的角色与通用滤波公式（15.3）或者隐马尔可夫模型中的滤波公式（15.10）是完全相同的。然而，因为高斯分布的特殊本质，使这些公式具有了某些附加的有趣性质。首先，我们可以把新的均值μt+1解释为新的观察zt+1和原来均值μt的一个简单的加权平均。如果观察不可靠，那么很大，我们更关注旧的均值；如果旧的均值不可靠（即很大），或者这个过程高度不可预测（很大），那么我们更关注于观察值。其次，注意到方差的更新是与观察无关的。因此我们可以在事先计算出方差值的序列。第三，方差值的序列很快收敛到一个固定的值，并且这个值只与和有关，因此能够大大简化后续的计算过程（参见习题15.7）。