证券组合的效用分析

马柯维茨在建立了以收益和风险的投资组合模型的基础上，推导出投资组合的有效集。为了更好地说明马柯维茨有效集理论，有必要先说明一下证券组合的投资效用函数。

（一）证券组合的效用函数

证券组合的效用是指一定证券组合的收益所产生的心理效应，它是衡量投资者对不同证券组合偏好程度的一种基本尺度。由于不同投资者具有不同的投资偏好，他们对同一证券组合的优劣评判也不一致，如有人比较喜欢冒风险，有人则讨厌风险。因此，要进行证券组合分析并求出最优的证券组合，必须首先研究证券组合的效用问题。

不同证券组合的收益率产生不同的效用值，效用与证券收益率的对应关系就是效用函数。例如：

其中，R代表收益率，U代表效用，当收益率为10%时，则证券组合的效用为3.8个单位。

由于证券收益的不确定性，效用函数所反映的证券组合效用也是不确定的。这时，就有必要计算效用的期望值。效用期望值的公式为：

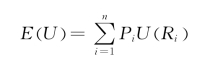
式中，E（U）代表效用的期望值；Pi代表与收益率相对应的概率；Ri代表各种收益率。

（二）效用函数的基本类型

由于投资者对风险的态度不同，导致效用函数的类型也不尽相同，具体可分为凸性效用函数、凹性效用函数和线性效用函数三种。

1.凸性效用函数

若效用函数对于任意的证券组合收益率Rx都能满足：

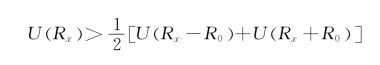
则称此效用函数为凸性效用函数，如图7.5所示。

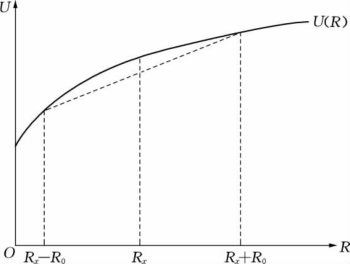
图7.5　凸性效用函数

对凸性效用函数来说，它的斜率随着收益率的增加而变得越来越小，即可得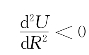，。其经济含义是投资收益率的边际效用递减，即投资者不愿冒风险。一般而言，效用函数越凸，投资者越规避风险。

2.凹性效用函数

若对于任意的证券组合收益率Rx都能满足：

则称此函数为凹性效用函数，如图7.6所示。

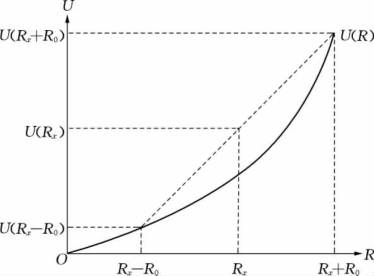
图7.6　凹性效用函数

对于凹性效用函数来说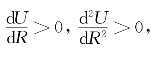也就是说投资者收益率的边际效用递增，即凹性效用函数的投资者是喜欢风险的。

3.线性效用函数

线性效用函数上的点满足：

不难发现，其投资收益率的边际效用是一个常数，投资者属于风险中性者。线性效用函数如图7.7所示。

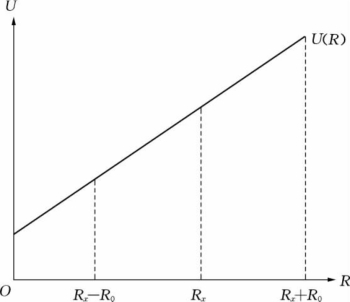
图7.7　线性效用函数

（三）效用函数期望无差异曲线

我们已经给出证券组合效用的期望值公式，即：

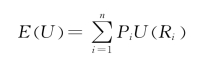
由上式可知，一定的证券组合对应着一定的效用期望值。由于从理论上讲存在无数种组合方案，因此，有可能找到一些证券组合，在效用函数一定的条件下，这些组合都有相等的效用期望值。由于这些证券组合能产生相等的期望值，说明对于相应的投资者而言，这些证券组合是没有区别的，都是可取的。如果能将产生相同效用期望值的各种证券组合对应的收益率期望值和标准差列出，在E（ R）和σ坐标系中描述出它们对应的点，并用平滑的曲线将这些点连接起来，就得到了效用无差异曲线，或称风险收益无差异曲线，如图7.8所示^[1]。

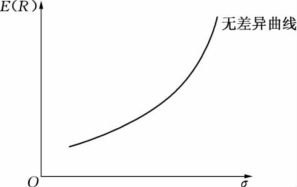
图7.8　效用期望无差异曲线

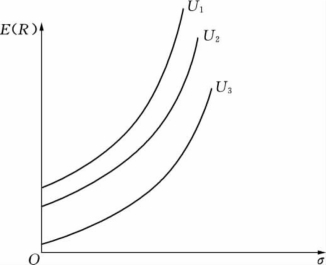
图7.9　高度风险回避型

图7.10　中度风险回避型

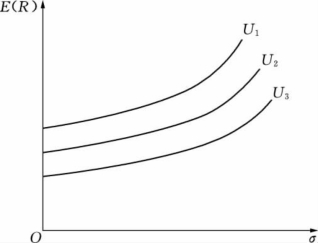
图7.11　轻度风险回避型

由于效用期望值可以有许多个，因此，投资者的无差异曲线也有许多条。当然，投资者会选择能提供最大效用期望值的无差异曲线作为投资的证券组合目标。图7.9、图7.10和图7.11分别表示不同风险回避者的无差异曲线。我们通常假设所有的投资者都是风险回避者，一些投资者可能是高度风险回避者，一些则可能是轻度风险回避者，另一些则可能介于两者之间。风险回避越高的投资者，他的无差异曲线就越陡峭，斜率越大。

无差异曲线有以下两个重要的特点：

第一，位于同一条无差异曲线上的所有证券组合，对投资者都具有相同的偏好。这一特点反映在图上就是无差异曲线之间不能相交。

第二，在坐标系中，越是位于西北方向的无差异曲线上的证券组合越为投资者所偏好。如图7.12所示。A、B、C三种证券组合，投资者对A、B有相同的偏好。但投资者更偏好于C，因为证券组合C位于较高的效用无差异曲线上。对于A来说，C组合有更大的预期收益率弥补它较高的标准差，对B来说，C则有更小的标准差来弥补它较小的预期收益。

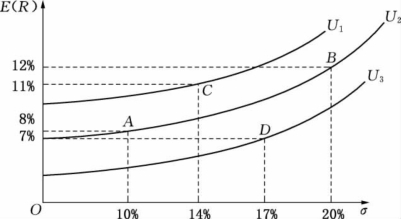
图7.12　无差异曲线的特点