函数的对称性

函数的对称性

祝兵

函数的性质是竞赛和高考的重点与热点，函数的对称性是函数的一个基本性质，对称关系不仅广泛存在于数学问题之中，而且利用对称性往往能更简捷地使问题得到解决，对称关系还充分体现了数学之美。本文拟通过函数自身的对称性和不同函数之间的对称性这两个方面来探讨函数与对称有关的性质。

一、函数自身的对称性探究

定理1．函数y= f(x)的图像关于点A(a，b)对称的充要条件是

f(x)+ f(2a－x)= 2b

证明:(必要性)设点P(x，y)是y= f(x)图像上任一点，∵点P( x，y)关于点A(a，b)的对称点P'(2a－x，2b－y)也在y= f(x)图像上，∴2b－y= f(2a－x)

即y+ f(2a－x)=2b故f(x)+ f(2a－x)= 2b，必要性得证。

(充分性)设点P(x₀，y₀)是y= f(x)图像上任一点，则y₀= f(x₀)

∵f(x)+ f(2a－x)= 2b∴f(x₀)+ f(2a－x₀)= 2b，即2b－y₀= f(2a－x₀)。

故点P'(2a－x₀，2b－y₀)也在y= f(x)图像上，而点P与点P'关于点A(a，b)对称，充分性得征。

推论1:函数y= f(x)的图像关于原点O对称的充要条件是f(x)+ f(－x)= 0

推论2:函数y= f(x)的图像关于点(a、o)对称的充要条件是f(x)=－f(2a－x)

推论3:函数y= f(a+ x)是奇函数的充要条件是f(x)关于点(a、0)对称。

定理2:函数y= f(x)的图像关于直线对称的充要条件是f(a+ x)= f(b－x)即f(a+ b－x)= f(x)

推论1:函数y= f(x)的图像关于直线x= a对称的充要条件是

f(a+ x)= f(a－x)即f(x)= f(2a－x)

推论2:函数y= f(x)的图像关于y轴对称的充要条件是f(x)= f(－x)

推论3:函数y= f(x+ a)是偶函数的充要条件是f(x)关于x= a对称

定理3．①若函数y= f(x)图像同时关于点A(a，c)和点B(b，c)成中心对称(a≠b)，则y= f(x)是周期函数，且2| a－b|是其一个周期。

②若函数y= f(x)图像同时关于直线x= a和直线x= b成轴对称(a≠b)，则y= f(x)是周期函数，且2| a－b|是其一个周期。

③若函数y= f(x)图像既关于点A(a，c)成中心对称又关于直线x= b成轴对称(a≠b)，则y= f(x)是周期函数，且4| a－b|是其一个周期。

①②的证明留给读者，以下给出③的证明:

∵函数y= f(x)图像既关于点A(a，c)成中心对称，

∴f(x)+ f(2a－x)=2c，用2b－x代x得:

f(2b－x)+ f［2a－(2b－x)］=2c………………(*)

又∵函数y= f(x)图像直线x= b成轴对称，

∴f(2b－x)= f(x)代入(*)得:

f(x)= 2c－f［2(a－b)+ x］…………(＊＊)，用2(a－b)－x代x得

f［2(a－b)+ x］= 2c－f［4(a－b)+ x］代入(＊＊)得:

f(x)= f［4(a－b)+ x］，故y= f(x)是周期函数，且4| a－b|是其一个周期。

二、不同函数对称性的探究

定理4:复合函数y= f(a+ x)与y= f(b－x)关于直线轴对称

推论:复合函数y= f(a+ x)与y= f(a－x)关于y轴对称

定理5:复合函数y= f(a+ x)与y=－f(b－x)关于中心对称。

推论:复合函数y= f(a+ x)与y=－f(a－x)关于原点对称。

现给出定理3的证明:令(m、n)是y= f(a+ x)上任意一点，则n= f(a+m)，令b－x=m+ a，x= b－m－a则(b－m－a，n)为y= f(b－x)上相应的一点。又点(m、n)与点(b－m－a，n)关于对称，所以y= f(a+ x)与y= f(b－x)关于直线轴对称。

定理4的证明留给读者。

定理6:函数y= f(x)与y= 2b－f(2a－x)的图像关于点A(a，b)成中心对称。

定理7:①函数y= f(x)与y= f(2a－x)的图像关于直线x= a成轴对称。

②函数y= f(x)与a－x= f(a－y)的图像关于直线x+ y= a成轴对称。

③函数y= f(x)与x－a= f(y+ a)的图像关于直线x－y= a成轴对称。

定理6与定理7中的①②证明留给读者，现证定理7中的③

设点P(x₀，y₀)是y= f(x)图像上任一点，则y₀= f(x₀)。记点P( x，y)关于直线x－y= a的轴对称点为P^‘(x₁，y₁)，则x₁= a+ y₀，y₁= x₀－a，∴x₀= a+ y₁，y₀= x₁－a代入y₀= f(x₀)之中得x₁－a= f(a+ y₁)∴点P^‘(x₁，y₁)在函数x－a= f(y+ a)的图像上。

同理可证:函数x－a= f(y+ a)的图像上任一点关于直线x－y= a的轴对称点也在函数y= f(x)的图像上。故定理7中的③成立。

推论:函数y= f(x)的图像与x= f(y)的图像关于直线x= y成轴对称。

三、三角函数图像的对称性列表

注:上表中k∈Z

四、函数对称性应用举例

例1　定义在R上的函数f(x)满足:f(10+ x)为偶函数，且f(20－x)=－f(20+ x)，则f(x)一定是(　　)

A．是偶函数，也是周期函数　　B．是偶函数，但不是周期函数

C．是奇函数，也是周期函数　　D．是奇函数，但不是周期函数

解:∵f(10+ x)为偶函数，∴f(10+ x)= f(10－x)．f(x)是关于x=10对称。

又∵f(20－x)=－f(20+ x)∴f(x)关于(20、0)中心对称。且T=40，因此f(x)是以40为其一个周期的周期函数，f(x)也关于(0、0)中心对称，因此f(x)还是一个奇函数。

故选(C)

例2　设定义域为R的函数y= f(x)、y= g(x)都有反函数，并且f(x－1)和g^－1(x－2)函数的图像关于直线y= x对称，若g(5)= 1999，那么f(4)=(　　)。

A．1999;　　B．2000　　C．2001　　D．2002。

解:∵y= f(x－1)和y= g^－1(x－2)函数的图像关于直线y= x对称，

∴y= g^－1(x－2)反函数是y= f(x－1)，而y= g^－1(x－2)的反函数是:y= 2+ g(x)，∴f(x－1)= 2+ g(x)，∴有f(5－1)= 2+ g(5)=2001

故f(4)= 2001，应选(C)

例3　设f(x)是定义在R上的偶函数，且f(1+ x)= f(1－x)，当－1≤x≤0时，f(x)=，则f(8．6)=＿＿。

解:∵f(x)是定义在R上的偶函数∴x= 0是y= f(x)对称轴;

又∵f(1+ x)= f(1－x)∴x= 1也是y= f(x)对称轴。故y= f(x)是以2为周期的周期函数，∴f(8．6)= f(8+ 0．6)= f(0．6)= f(－0．6)= 0．3

例4　函数的图像的一条对称轴的方程是(　　)(92全国高考理)

A．x=　　B．x=　　C．x=　　D．x=

解:函数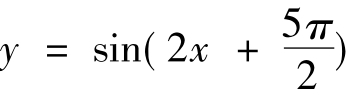的图像的所有对称轴的方程是

∴，显然取k= 1时的对称轴方程是故选(A)

例5　设f(x)是定义在R上的奇函数，且f(x+ 2)=－f(x)，当0≤x≤1时，f(x)= x，则f(7．5)=(　　)

A．0．5　　B．－0．5　　C．1．5　　D．－1．5

解:∵y= f(x)是定义在R上的奇函数，∴点(0，0)是其对称中心;

又∵f(x+2)=－f(x)= f(－x)，即f(1+ x)= f(1－x)，∴直线x= 1是y= f(x)对称轴，故y= f(x)是周期为2的周期函数。

∴f(7．5)= f(8－0．5)= f(－0．5)=－f(0．5)=－0．5故选(B)